《2025年作业本江西教育出版社七年级数学上册人教版》

1. 计算:13+(-17)+27+(-13)=10.

答案： 解：13+(-17)+27+(-13)
=(13+27)+[(-17)+(-13)]
=40+(-30)
=10
10

计算:(-6.2)+(+5.3)+(-3.8)+(+4.7).
解:原式= (-6.2)+(-3.8)+(+5.3)+(+4.7)(加法交换律)
=[(-6.2)+(-3.8)]+[(+5.3)+(+4.7)](加法结合律).

答案： 【解析】：
此题考查了有理数的加法运算律，特别是加法的交换律和结合律。
首先，我们通过改变加数的顺序，将负数与负数相加，正数与正数相加，这运用了加法的交换律。
然后，我们通过加括号来改变运算顺序，先进行每对括号内的加法运算，这运用了加法的结合律。
【答案】：
加法交换律；加法结合律

3. 一个数是20,另一个数比15的相反数小2,这两个数的和为3.

答案： 【解析】：
首先，根据题意，一个数是$20$。
接着，我们需要找出另一个数。根据题目，另一个数比$15$的相反数小$2$。
$15$的相反数是$-15$，所以另一个数为$-15 - 2 = -17$。
最后，我们需要求出这两个数的和。根据有理数加法法则，$20 + (-17) = 3$。
【答案】：
$3$

4. 若a+b= 2024,c+d= -2025,则a+3+c+(-3)+b+d= -1.

答案： 【解析】：
本题主要考察有理数的加法运算以及代数式的合并同类项。
首先，我们可以将原式中的各项进行合并，以便使用给定的等式$a+b=2024$和$c+d=-2025$。
原式可以写为：
$a + 3 + c + (-3) + b + d = (a + b) + (c + d) + 3 - 3$，
然后，我们可以将$a+b$和$c+d$分别替换为给定的等式：
$= 2024 + (-2025) + 3 - 3$，
接着，我们可以进行简单的有理数加法运算来求解这个表达式：
$= 2024 - 2025 + 0$，
$= -1$。
【答案】：
$-1$。

5. 计算.
(1)11+(-3)+(-5)+2;
(2)$|-23|+|-43|+(-16)+0$;
(3)$\frac{1}{2}+(-\frac{2}{3})+\frac{4}{7}+(-\frac{1}{2})+(-\frac{1}{3})$.

答案： 【解析】：
本题主要考察有理数的加法运算，包括正数与负数的相加，绝对值的计算，以及分数的相加。
(1) 对于第一个表达式，需要按照加法法则进行计算，特别注意负数的相加。
(2) 第二个表达式涉及到绝对值的计算，需要先求出每个数的绝对值，再进行加法运算。
(3) 第三个表达式是分数的相加，需要注意找公分母，以及正负数的相加规则。
【答案】：
(1)
解：
$11 + (-3) + (-5) + 2$
$= 11 - 3 - 5 + 2$
$= 5$
(2)
解：
$|-23| + |-43| + (-16) + 0$
$= 23 + 43 - 16 + 0$
$= 50$
(3)
解：
$\frac{1}{2} + (-\frac{2}{3}) + \frac{4}{7} + (-\frac{1}{2}) + (-\frac{1}{3})$
$= \frac{1}{2} - \frac{1}{2} - \frac{2}{3} - \frac{1}{3} + \frac{4}{7}$
$= 0 - 1 + \frac{4}{7}$
$= -\frac{3}{7}$

6. 用简便方法计算.
(1)24+(-18)+6+(-22);
(2)$1.125+(-3\frac{2}{5})+(-\frac{1}{8})+(-0.6)$;
(3)(-2.48)+(+4.33)+(-7.52)+(-4.33).

答案： 【解析】：
本题主要考察有理数的加法运算，特别是如何利用加法的交换律和结合律简化计算。
(1) 对于第一题，可以先将正数和负数分别相加，以简化计算。
(2) 对于第二题，可以先将小数和分数转化为相同的数值形式（如小数或分数），再利用加法的交换律和结合律进行计算。
(3) 对于第三题，可以先将互为相反数的数相加，以简化计算。
【答案】：
(1)
解：
原式 = 24 + (-18) + 6 + (-22)
= (24 + 6) + [(-18) + (-22)] （利用加法的交换律和结合律）
= 30 + (-40)
= -10
(2)
解：
原式$ = 1.125 + (-3\frac{2}{5}) + (-\frac{1}{8}) + (-0.6)$
= 1.125 + (-3.4) + (-0.125) + (-0.6) （将分数转化为小数）
= [1.125 + (-0.125)] + [(-3.4) + (-0.6)] （利用加法的交换律和结合律）
= 1 + (-4)
= -3
(3)
解：
原式 = (-2.48) + (+4.33) + (-7.52) + (-4.33)
= [(-2.48) + (-7.52)] + [(+4.33) + (-4.33)] （利用加法的交换律和结合律）
= -10 + 0
= -10

7. 一名病人早晨8时的体温是39.7℃,下表是该病人24小时的体温变化(用正数记录体温比前一时刻的上升数,用负数记录体温比前一时刻的下降数).
(单位：℃)

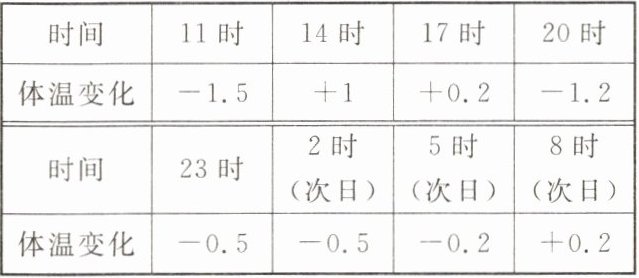
(1)次日上午8时,这名病人的体温是多少摄氏度?
(2)在表格中,哪个时刻这个病人的体温最高？最高是多少摄氏度？哪个时刻这个病人的体温最低？最低是多少摄氏度？
(3)若人体正常体温是37℃,则从体温看,这名病人的病情是在恶化还是在好转？

答案： 【解析】：
本题主要考查了有理数的加法运算在实际问题中的应用，通过逐步计算不同时刻的体温来回答问题。
（1）要求次日上午$8$时病人的体温，需要用早晨$8$时的体温$39.7^{\circ}C$，依次加上从早晨$8$时到次日上午$8$时各个时间段的体温变化值。
（2）要找出体温最高和最低的时刻及对应体温，需要依次计算出各个时刻的体温，然后进行比较。
（3）根据计算出的体温与人体正常体温$37^{\circ}C$进行比较，判断病情的变化情况。
【答案】：
(1)解：
已知早晨$8$时体温是$39.7^{\circ}C$，
$11$时体温变化为$-1.5$，则$11$时体温为$39.7 + (-1.5)=39.7 - 1.5 = 38.2^{\circ}C$；
$14$时体温变化为$ + 1$，则$14$时体温为$38.2 + 1 = 39.2^{\circ}C$；
$17$时体温变化为$ + 0.2$，则$17$时体温为$39.2 + 0.2 = 39.4^{\circ}C$；
$20$时体温变化为$-1.2$，则$20$时体温为$39.4 + (-1.2)=39.4 - 1.2 = 38.2^{\circ}C$；
$23$时体温变化为$-0.5$，则$23$时体温为$38.2 + (-0.5)=38.2 - 0.5 = 37.7^{\circ}C$；
$2$时（次日）体温变化为$-0.5$，则$2$时（次日）体温为$37.7 + (-0.5)=37.7 - 0.5 = 37.2^{\circ}C$；
$5$时（次日）体温变化为$-0.2$，则$5$时（次日）体温为$37.2 + (-0.2)=37.2 - 0.2 = 37^{\circ}C$；
$8$时（次日）体温变化为$ + 0.2$，则$8$时（次日）体温为$37 + 0.2 = 37.2^{\circ}C$。
所以次日上午$8$时，这名病人的体温是$37.2^{\circ}C$。
(2)由（1）的计算可知：
$11$时体温$38.2^{\circ}C$；$14$时体温$39.2^{\circ}C$；$17$时体温$39.4^{\circ}C$；$20$时体温$38.2^{\circ}C$；$23$时体温$37.7^{\circ}C$；$2$时（次日）体温$37.2^{\circ}C$；$5$时（次日）体温$37^{\circ}C$；$8$时（次日）体温$37.2^{\circ}C$。
比较可得$39.4\gt39.2\gt38.2\gt37.7\gt37.2\gt37$，
所以$17$时这个病人的体温最高，最高是$39.4^{\circ}C$；$5$时（次日）这个病人的体温最低，最低是$37^{\circ}C$。
(3)人体正常体温是$37^{\circ}C$，由（1）（2）计算可知，病人的体温从最初的$39.7^{\circ}C$逐渐下降，到次日$5$时达到$37^{\circ}C$（接近正常体温），之后虽有波动但整体趋于稳定且接近正常体温。
所以从体温看，这名病人的病情在好转。