《2025年作业本江西教育出版社七年级数学上册人教版》

1. 某车间有28名工人,每名工人每天生产镜架60个或者镜片90片.为使每天生产的镜架和镜片刚好配套,则安排生产镜片的工人人数是(A)
A.16
B.15
C.20
D.18

答案： 【解析】：
本题考查了实际问题与一元一次方程的应用。
设安排生产镜片的工人人数为$x$人，则生产镜架的工人人数为$(28 - x)$人。
根据题意，每名生产镜片的工人每天能生产90片镜片，所以$x$名工人每天能生产$90x$片镜片；
每名生产镜架的工人每天能生产60个镜架，所以$(28 - x)$名工人每天能生产$60(28 - x)$个镜架。
由于一个镜架需要两个镜片，所以每天生产的镜片数量应该是镜架数量的两倍，即：
$2 × 60(28 - x) = 90x$
解这个方程，我们得到：
$120(28 - x) = 90x$
$3360 - 120x = 90x$
$210x = 3360$
$x = 16$
所以，安排生产镜片的工人人数是16人。
【答案】：A

2. 录入一篇书稿,甲单独录入需要$\frac{1}{4}$ h,乙单独录入需要0.5 h,甲、乙两人合作,$\frac{1}{6}$h可以完成.

答案： 解：设甲、乙两人合作，$x$ h可以完成。
把这篇书稿的工作量看作单位“1”。
甲单独录入需要$\frac{1}{4}$ h，甲的工作效率为$1÷\frac{1}{4}=4$（单位/h）；
乙单独录入需要0.5 h，即$\frac{1}{2}$ h，乙的工作效率为$1÷\frac{1}{2}=2$（单位/h）。
根据工作总量=工作效率×工作时间，可列方程：
$(4 + 2)x=1$
$6x=1$
$x=\frac{1}{6}$
答：甲、乙两人合作，$\frac{1}{6}$ h可以完成。

3. 某单位为一中学捐赠了一批新桌椅,学校组织七年级200名学生搬桌椅.规定一人一次搬两把椅子,两人一次搬一张桌子,每人限搬一次,最多可搬桌椅(一桌一椅为一套)80套.

答案： 解：设搬桌子的人数为$x$人，则搬椅子的人数为$(200 - x)$人。
根据题意，两人一次搬一张桌子，可得桌子数量为$\frac{x}{2}$张；一人一次搬两把椅子，可得椅子数量为$2(200 - x)$把。
因为桌椅一套为一桌一椅，所以桌子数量和椅子数量应相等时，套数最多，即：
$\frac{x}{2} = 2(200 - x)$
解方程：
$x = 4(200 - x)$
$x = 800 - 4x$
$x + 4x = 800$
$5x = 800$
$x = 160$
则桌子数量为$\frac{160}{2} = 80$张，椅子数量为$2(200 - 160) = 80$把。
所以最多可搬桌椅$80$套。
答案：$80$

4. 某小组种植一批树苗,若每人种10棵,则剩6棵未种；若每人种12棵,则缺6棵.该小组共种植66棵树苗.

答案： 解：设该小组有$x$人。
根据题意，得$10x + 6 = 12x - 6$。
解得$x = 6$。
则树苗总数为$10×6 + 6 = 66$（棵）。
66

5. 一项工程单独完成,甲队要30天,乙队要25天.现两队同时开始合作,中途两队都休息了一段时间,这样用了16天才完成任务.已知甲中途休息了4天,则乙中途休息了几天？

答案： 解：设乙中途休息了$x$天。
甲队工作效率：$\frac{1}{30}$，乙队工作效率：$\frac{1}{25}$。
甲工作时间：$16 - 4 = 12$（天），乙工作时间：$16 - x$（天）。
依题意得：$\frac{1}{30}×12 + \frac{1}{25}×(16 - x) = 1$
$\frac{12}{30} + \frac{16 - x}{25} = 1$
$\frac{2}{5} + \frac{16 - x}{25} = 1$
两边同乘25：$10 + 16 - x = 25$
$26 - x = 25$
$x = 1$
答：乙中途休息了1天。

6. 如图所示,将某种规格的长方形纸板按照图①、图②所示的两种方法裁剪,分别可裁得2块小长方形纸板或3块小正方形纸板.4块相同的小长方形纸板和1块小正方形纸板可做成图③所示的无盖长方体纸盒,而有盖长方体纸盒则需要4块相同的小长方形纸板和2块小正方形纸板.现有这种规格的长方形纸板21张.

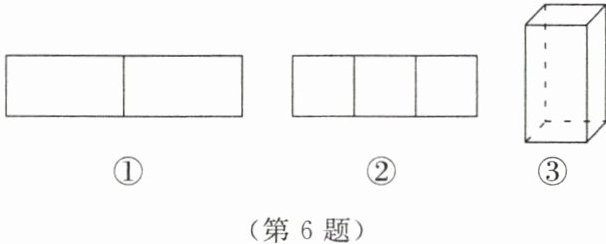
(1)怎样裁剪这21张纸板可制成的无盖纸盒数最多？最多能做多少个？
(2)若要求加工方另外制成有盖长方体纸盒30个,则加工方还需要购进同样规格的长方形纸板多少张？

答案：
(1)设用$x$张纸板按方法①裁剪，则用$(21 - x)$张按方法②裁剪。
每个无盖纸盒需4个小长方形和1个小正方形，
小长方形总数：$2x$，小正方形总数：$3(21 - x)$。
纸盒数$y$满足：$y \leq \frac{2x}{4}$且$y \leq 3(21 - x)$，即$y \leq \frac{x}{2}$且$y \leq 63 - 3x$。
令$\frac{x}{2} = 63 - 3x$，解得$x = 18$。
此时$y = \frac{18}{2} = 9$。
答：用18张按方法①，3张按方法②裁剪，最多做9个无盖纸盒。
(2)30个有盖纸盒需小长方形：$30×4 = 120$，小正方形：$30×2 = 60$。
设需购进$m$张纸板，其中$a$张按①裁剪，$(m - a)$张按②裁剪。
则$2a \geq 120$，$3(m - a) \geq 60$。
由$2a = 120$得$a = 60$，代入$3(m - 60) = 60$，解得$m = 80$。
答：还需购进80张纸板。
(1)最多能做9个；
(2)还需要购进80张。