第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
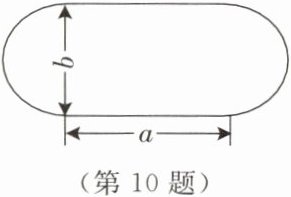
10. 某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a m,半圆形弯道的直径为 b m.
(1)用含 a,b 的代数式表示这条跑道的周长.
(2)当 a= 67.4,b= 52.6 时,求这条跑道的周长(π取 3,结果取整数).
(1)用含 a,b 的代数式表示这条跑道的周长.
(2)当 a= 67.4,b= 52.6 时,求这条跑道的周长(π取 3,结果取整数).

答案:
【解析】:
(1) 跑道由两段直道和两段半圆形的弯道组成,直道的长为$a$米,半圆形弯道的直径为$b$米,两段半圆形弯道合起来是一个圆,其周长为圆的周长公式$πb$,所以这条跑道的周长为$2a+πb$。
(2) 将$a = 67.4$,$b = 52.6$,$π=3$代入(1)中所求式子,可求出跑道的周长,最后结果按要求取整数。
【答案】:
解:
(1) $2a + πb$;
(2) 当$a = 67.4$,$b = 52.6$,$π=3$时,
$2a + πb$
$= 2×67.4 + 3×52.6$
$= 134.8 + 157.8$
$= 292.6$
$\approx 293$(m)
答:这条跑道的周长约为293m。
(1) 跑道由两段直道和两段半圆形的弯道组成,直道的长为$a$米,半圆形弯道的直径为$b$米,两段半圆形弯道合起来是一个圆,其周长为圆的周长公式$πb$,所以这条跑道的周长为$2a+πb$。
(2) 将$a = 67.4$,$b = 52.6$,$π=3$代入(1)中所求式子,可求出跑道的周长,最后结果按要求取整数。
【答案】:
解:
(1) $2a + πb$;
(2) 当$a = 67.4$,$b = 52.6$,$π=3$时,
$2a + πb$
$= 2×67.4 + 3×52.6$
$= 134.8 + 157.8$
$= 292.6$
$\approx 293$(m)
答:这条跑道的周长约为293m。
11. 综合与实践.
请同学们用数学的眼光认真观察下面表格中的两个代数式及其相应的值,通过数学的思维进行思考,并用数学的语言解答下列问题.
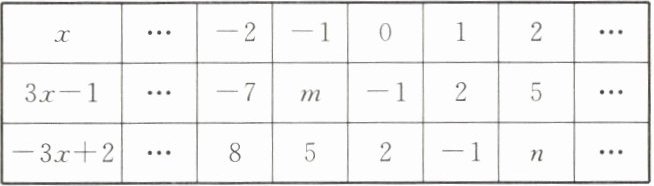
(1)【初步感知】根据表中信息可知 m=
(2)【归纳规律】表中代数式$3x - 1$的值的变化规律是 x 的值每增加 1,代数式$3x - 1$的值就增加 3. 类似地,代数式$-3x + 2$的值的变化规律是什么?
(3)【拓展应用】当 x 的值每增加 2 时,猜想代数式$-5x - 1$的值会怎样变化. 请通过计算加以验证.
猜想:当 x 的值每增加 2 时,代数式$-5x - 1$的值减少 10。
验证:设 x=a 时,代数式的值为$-5a - 1$;当 x=a + 2 时,代数式的值为$-5(a + 2)-1=-5a - 10 - 1=-5a - 11$。两者的差为$(-5a - 1)-(-5a - 11)=10$,即值减少 10。
请同学们用数学的眼光认真观察下面表格中的两个代数式及其相应的值,通过数学的思维进行思考,并用数学的语言解答下列问题.

(1)【初步感知】根据表中信息可知 m=
-4
,n=-4
.(2)【归纳规律】表中代数式$3x - 1$的值的变化规律是 x 的值每增加 1,代数式$3x - 1$的值就增加 3. 类似地,代数式$-3x + 2$的值的变化规律是什么?
代数式$-3x + 2$的值的变化规律是:x 的值每增加 1,代数式$-3x + 2$的值就减少 3。
(3)【拓展应用】当 x 的值每增加 2 时,猜想代数式$-5x - 1$的值会怎样变化. 请通过计算加以验证.
猜想:当 x 的值每增加 2 时,代数式$-5x - 1$的值减少 10。
验证:设 x=a 时,代数式的值为$-5a - 1$;当 x=a + 2 时,代数式的值为$-5(a + 2)-1=-5a - 10 - 1=-5a - 11$。两者的差为$(-5a - 1)-(-5a - 11)=10$,即值减少 10。
答案:
(1) 当 $x=-1$ 时,$3x - 1 = 3×(-1)-1=-4$,所以 $m=-4$;当 $x=2$ 时,$-3x + 2=-3×2 + 2=-4$,所以 $n=-4$。
(2) 代数式 $-3x + 2$ 的值的变化规律是:$x$ 的值每增加 1,代数式 $-3x + 2$ 的值就减少 3。
(3) 猜想:当 $x$ 的值每增加 2 时,代数式 $-5x - 1$ 的值减少 10。
验证:设 $x=a$ 时,代数式的值为 $-5a - 1$;当 $x=a + 2$ 时,代数式的值为 $-5(a + 2)-1=-5a - 10 - 1=-5a - 11$。两者的差为 $(-5a - 1)-(-5a - 11)=10$,即值减少 10。
(1) 当 $x=-1$ 时,$3x - 1 = 3×(-1)-1=-4$,所以 $m=-4$;当 $x=2$ 时,$-3x + 2=-3×2 + 2=-4$,所以 $n=-4$。
(2) 代数式 $-3x + 2$ 的值的变化规律是:$x$ 的值每增加 1,代数式 $-3x + 2$ 的值就减少 3。
(3) 猜想:当 $x$ 的值每增加 2 时,代数式 $-5x - 1$ 的值减少 10。
验证:设 $x=a$ 时,代数式的值为 $-5a - 1$;当 $x=a + 2$ 时,代数式的值为 $-5(a + 2)-1=-5a - 10 - 1=-5a - 11$。两者的差为 $(-5a - 1)-(-5a - 11)=10$,即值减少 10。
查看更多完整答案,请扫码查看


