《2025年作业本江西教育出版社七年级数学上册人教版》

1. 如果把“盈利 100 元”记作“+100 元”,那么“亏损 80 元”可记作“-80元”.

答案： 【解析】：
本题考查正负数在实际生活中的应用。题目中提到“盈利100元”记作“+100元”，这里的“+”表示盈利。由此我们可以推断，亏损应该用负数来表示。因此，“亏损80元”就应该记作具有相反意义的量，即“-80元”。
【答案】：
-80

2. 有下列数字：2.$\dot{6}$,$-0.010010001$,$\pi$,$-8\frac{1}{4}$,$\frac{22}{7}$,15,$-2$. 其中整数有$a$个,有理数有$b$个,则$a + b= $8.

答案： 【解析】：
本题主要考察的是对于整数和有理数的识别以及计数。
首先，需要明确整数和有理数的定义。
整数包括正整数、零和负整数。
有理数是可以表示为两个整数的比的数，其中分母不为0。
在给定的数字中：
$2.\dot{6}$ 是一个循环小数，它等于$\frac{8}{3}$，是有理数但不是整数。
$-0.010010001$ 是一个有限小数，可以转换为分数形式，所以是有理数但不是整数。
$\pi$ 是一个无理数，既不是整数也不是有理数。
$-8\frac{1}{4}$ 是一个带分数，可以转换为假分数，所以是有理数但不是整数。
$\frac{22}{7}$ 是一个分数形式，所以是有理数但不是整数。
$15$ 是正整数，所以也是有理数。
$-2$ 是负整数，所以也是有理数。
统计整数和有理数的个数：
整数有 $15, -2$，共2个，所以 $a = 2$。
有理数有 $2.\dot{6}, -0.010010001, -8\frac{1}{4}, \frac{22}{7}, 15, -2$，共6个，所以 $b = 6$。
最后计算 $a + b = 2 + 6 = 8$。
【答案】：
$8$

3. 一只蚂蚁由数轴上表示$-2$的点先向右爬3个单位长度,再向左爬5个单位长度,此时蚂蚁所在的位置表示的数是-4.

答案： 解：蚂蚁初始位置表示的数是$-2$。
向右爬3个单位长度后，位置表示的数为：$-2 + 3 = 1$。
再向左爬5个单位长度后，位置表示的数为：$1 - 5 = -4$。
$-4$

4. 若$a - 5与-1$互为相反数,则$a= $6.

答案： 【解析】：
本题主要考查相反数的定义。根据相反数的性质，两个数互为相反数当且仅当它们的和为0。因此，我们可以根据这一性质列出等式，并解出$a$的值。
【答案】：
解：
∵ $a - 5$ 与 $-1$ 互为相反数，
∴ $a - 5 + (-1) = 0$，
即 $a - 6 = 0$，
解得 $a = 6$。
故答案为：$6$。

5. 如图所示,将一把刻度尺放在数轴上,数轴的单位长度是1 cm. 若刻度尺上“1 cm”和“8 cm”分别对应数轴上的2和$x$,则$x$的值为9.

答案： 【解析】：
本题主要考查数轴上两点间的距离公式，即若数轴上两点所表示的数分别为$a$，$b$，则这两点间的距离为$\vert a - b\vert$。
已知刻度尺上“$1cm$”和“$8cm$”分别对应数轴上的$2$和$x$，那么这两点在数轴上的距离就等于刻度尺上对应的长度差，刻度尺上$1cm$到$8cm$的长度差为$8 - 1 = 7cm$，而在数轴上这两点的距离为$\vert x - 2\vert$，所以可得$\vert x - 2\vert=7$。
接下来求解绝对值方程$\vert x - 2\vert=7$，根据绝对值的定义，绝对值是指一个数在数轴上所对应点到原点的距离，所以绝对值为$7$的数有两个，即$x - 2 = 7$或$x - 2 = -7$。
当$x - 2 = 7$时，方程两边同时加$2$，可得$x = 7 + 2 = 9$；
当$x - 2 = -7$时，方程两边同时加$2$，可得$x = -7 + 2 = -5$。
但从图中可以看出，$x$对应的点在$2$的右侧，也就是$x\gt2$，所以$x = -5$不符合题意，舍去。
因此，$x$的值为$9$。
【答案】：
$9$

6. 如果$|a| = 3$,$|b| = 1$,且$a ＞ b$,那么$a$的值为3,$b$的值为1或-1.

答案： 解：因为|a|=3，所以a=±3；
因为|b|=1，所以b=±1。
又因为a＞b，
当a=3时，b=1或b=-1均满足条件；
当a=-3时，-3＞1和-3＞-1均不成立，故a=-3舍去。
所以a=3，b=1或b=-1。

7. 如图所示,点$A$,$B$在数轴上,点$C表示|-3.5|$,点$D表示-(-2)$,点$E表示-2\frac{1}{2}$.

(1)点$A$表示的数为-1,点$B$表示的数为3.
(2)在数轴上标出点$C$,$D$,$E$,并按从小到大的顺序用“＜”连接这五个数.
在数轴上标出点C, D, E后，按从小到大的顺序排列为：-2.5 ＜ -1 ＜ 2 ＜ 3 ＜ 3.5。

答案： 【解析】：
本题主要考察数轴上数的表示以及绝对值、相反数的计算。
(1) 对于点A，它位于数轴上-1的位置，所以点A表示的数为-1。
对于点B，它位于数轴上3的位置，所以点B表示的数为3。
(2) 对于点C，它表示的是|-3.5|，根据绝对值的定义，|-3.5| = 3.5，所以在数轴上标出3.5的位置为点C。
对于点D，它表示的是-(-2)，根据相反数的定义，-(-2) = 2，所以在数轴上标出2的位置为点D。
对于点E，它表示的是$-2\frac{1}{2}$，即-2.5，所以在数轴上标出-2.5的位置为点E。
现在，我们有了五个数：-2.5（点E），-1（点A），2（点D），3（点B），3.5（点C）。
按从小到大的顺序排列这五个数，得到：-2.5 ＜ -1 ＜ 2 ＜ 3 ＜ 3.5。
【答案】：
(1) 点A表示的数为-1，点B表示的数为3。
(2) 在数轴上标出点C, D, E后，按从小到大的顺序排列为：-2.5 ＜ -1 ＜ 2 ＜ 3 ＜ 3.5。

8. 如图所示,将一根木棒放在数轴(单位长度为1)上,木棒左端与数轴上的点$A$重合,右端与数轴上的点$B$重合.

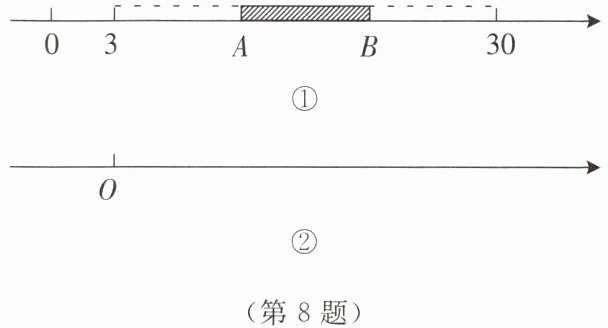
(1)将木棒沿数轴向右水平移动,当它的左端移动到点$B$时,它的右端在数轴上所对应的数为30；将木棒沿数轴向左水平移动,当它的右端移动到点$A$时,它的左端在数轴上所对应的数为3. 由此可得出这根木棒的长为9；图中点$A$所表示的数是12；点$B$所表示的数是21.
(2)受(1)的启发,请借助“数轴”这个工具解决下面的问题.
一天,爸爸对小明说：“我若是你现在这么大,你才刚出生；你若是我现在这么大,我就84岁啦！”求爸爸的年龄.(在图②中标出分析过程)
爸爸的年龄是56岁。

答案： 【解析】：
(1)考查数轴上点的移动和距离计算知识点。
设木棒长为$x$，点$A$表示的数为$a$，则点$B$表示的数为$a + x$。
当木棒沿数轴向右水平移动，左端移动到点$B$时，右端在数轴上所对应的数为$30$，此时木棒移动的距离为$x$，那么$a + x+x = 30$。
当木棒沿数轴向左水平移动，右端移动到点$A$时，左端在数轴上所对应的数为$3$，此时木棒移动的距离为$x$，那么$a - x = 3$。
联立方程组$\begin{cases}a + 2x = 30\\a - x = 3\end{cases}$，用第一个方程减去第二个方程可得：
$\begin{aligned}(a + 2x)-(a - x)&=30 - 3\\a + 2x - a + x&=27\\3x&=27\\x&=9\end{aligned}$
将$x = 9$代入$a - x = 3$，可得$a = 3 + 9 = 12$。
则点$B$表示的数为$a + x = 12 + 9 = 21$。
(2)考查利用数轴解决年龄问题知识点。
设小明现在年龄为$x$岁，爸爸现在年龄为$y$岁。
两人的年龄差是固定的，为$y - x$岁。
当爸爸是小明现在这么大时，即爸爸的年龄为$x$岁时，小明的年龄是刚出生$0$岁，此时两人的年龄差为$x - 0 = x$岁，也就是$y - x = x - 0$。
当小明是爸爸现在这么大时，即小明的年龄为$y$岁时，爸爸的年龄是$84$岁，此时两人的年龄差为$84 - y$岁，也就是$y - x = 84 - y$。
联立方程组$\begin{cases}y - x = x - 0\\y - x = 84 - y\end{cases}$，由第一个方程$y - x = x$可得$y = 2x$，将$y = 2x$代入第二个方程$y - x = 84 - y$中，得到$2x - x = 84 - 2x$，即$x = 84 - 2x$，移项可得$3x = 84$，解得$x = 28$。
把$x = 28$代入$y = 2x$，可得$y = 2×28 = 56$。
【答案】：
(1)$9$；$12$；$21$；
(2)爸爸的年龄是$56$岁。