《2025年作业本江西教育出版社七年级数学上册人教版》

16. 如图所示，四边形ABCD是一个长方形。
(1)根据图中数据，用含a，b，c的代数式表示图中阴影部分的面积S。
(2)当$a = 5$，$b = 4$，$c = 3$时，求S的值。

答案：
(1) 解：长方形ABCD的面积为 $a × b = ab$。
空白部分由两个三角形组成：
三角形ABE的面积：$\frac{1}{2} × 2 × c = c$
三角形ADF的面积：$\frac{1}{2} × a × (b - c) = \frac{1}{2}a(b - c)$
阴影部分面积 $S = ab - c - \frac{1}{2}a(b - c)$
化简得：$S = ab - c - \frac{1}{2}ab + \frac{1}{2}ac = \frac{1}{2}ab - c + \frac{1}{2}ac$
(2) 解：当 $a = 5$，$b = 4$，$c = 3$ 时，
$S = \frac{1}{2} × 5 × 4 - 3 + \frac{1}{2} × 5 × 3$
$= 10 - 3 + 7.5 = 14.5$
答案：
(1) $S = \frac{1}{2}ab + \frac{1}{2}ac - c$；
(2) $14.5$

17. 如图所示，在每个刻度为1个单位长度的数轴上，点A表示的数是$-2$。

(1)在数轴上标出原点，并指出点B所表示的数是4。
(2)在数轴上找出一点C，使它与点B的距离为2个单位长度，那么点C表示的数为2或6。
(3)在数轴上表示下列各数，并用“＜”号把这些数按从小到大的顺序连接起来。
$2.5$，$-4$，$-2\frac{1}{2}$，$|-1.5|$。
$-4 ＜ -2\frac{1}{2} ＜ |-1.5| ＜ 2.5$

答案： 【解析】：
(1) 从题目描述和数轴图可知，点A表示的数是$-2$，由于每个刻度为1个单位长度，从A点往右数2个单位即为原点。从原点再往右数4个单位即为点B，所以点B表示的数是4。
(2) 点C与点B的距离为2个单位长度，因此点C可以在点B的左侧或右侧。若在左侧，则点C表示的数为$4-2=2$；若在右侧，则点C表示的数为$4+2=6$。
(3) 需要比较的数有$2.5$，$-4$，$-2\frac{1}{2}$，$|-1.5|$。
其中$|-1.5|=1.5$，$-2\frac{1}{2}=-2.5$。
在数轴上，从左到右依次为：$-4$，$-2.5$，$1.5$，$2.5$。
因此，用“＜”号连接这些数的顺序为：$-4 ＜ -2\frac{1}{2} ＜ |-1.5| ＜ 2.5$。
【答案】：
(1) 原点在点A右侧2个单位长度处；点B所表示的数是4。
(2) 点C表示的数为2或6。
(3) $-4 ＜ -2\frac{1}{2} ＜ |-1.5| ＜ 2.5$。

18. 某超市购进一批白菜，共有20筐，以每筐25kg为标准，超过或不足的千克数分别用正、负数来表示，记录数据如下表所示：

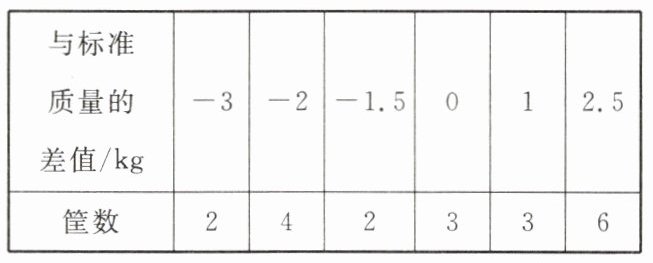
(1)与标准质量比较，20筐白菜总计超过或不足多少千克？
(2)若白菜每千克售价6元，则出售这20筐白菜可收入多少元？

答案：
(1)解：$(-3)×2 + (-2)×4 + (-1.5)×2 + 0×3 + 1×3 + 2.5×6$
$= -6 - 8 - 3 + 0 + 3 + 15$
$= (-6 - 8 - 3) + (0 + 3 + 15)$
$= -17 + 18$
$= 1$（千克）
答：20筐白菜总计超过1千克。
(2)解：$20×25 + 1 = 501$（千克）
$501×6 = 3006$（元）
答：出售这20筐白菜可收入3006元。