《2025年作业本江西教育出版社七年级数学上册人教版》

1. $-\frac{5}{7}$的相反数是$\frac{5}{7}$,绝对值是$\frac{5}{7}$.

答案： 【解析】：
本题考查的是相反数和绝对值的概念。
相反数的定义是：一个数与它的相反数相加等于零。
所以，$-\frac{5}{7}$的相反数就是与$-\frac{5}{7}$相加等于0的数，即$\frac{5}{7}$。
绝对值的定义是：一个数到0的距离。
对于任何负数a，其绝对值都是-a。
因此，$-\frac{5}{7}$的绝对值是$\frac{5}{7}$。
【答案】：
$\frac{5}{7}$；$\frac{5}{7}$

2. 比较大小,用“＞”或“＜”连接：$-|-\frac{4}{3}|$＜$-(-\frac{6}{5})$.

答案： 解：$-|-\frac{4}{3}|=-\frac{4}{3}$，$-(-\frac{6}{5})=\frac{6}{5}$，因为$-\frac{4}{3}＜\frac{6}{5}$，所以$-|-\frac{4}{3}|＜-(-\frac{6}{5})$。
＜

3. 如图所示,数轴的单位长度为1,如果点$A$,$C$表示的数的绝对值相等,那么点$B$表示的数是$-1$.

答案： 【解析】：
本题考查了数轴以及绝对值的知识，根据点$A$，$C$表示的数的绝对值相等，可以确定原点的位置，进而确定点$B$所表示的数。
确定原点的位置：
因为点$A$，$C$表示的数的绝对值相等，而绝对值相等的两个数所对应的点到原点的距离相等，所以在数轴上，点$A$与点$C$的中点就是原点。
已知数轴的单位长度为$1$，从点$A$到点$C$间隔了$4$个单位长度，那么点$A$与点$C$的中点到点$A$的距离为$4÷2 = 2$个单位长度，即原点在点$A$右侧$2$个单位长度处。
确定点$B$表示的数：
观察数轴可知，点$B$在原点左侧，且距离原点$1$个单位长度，根据数轴的定义，原点左侧的点表示的数为负数，距离原点几个单位长度就表示负几，所以点$B$表示的数是$-1$。
【答案】：
$-1$。

4. 若有理数$a$,$b$在数轴上的位置如图所示,则将有理数$|a|$,1,$b$按从小到大的顺序用“＜”连接起来是$1\lt |a| \lt b$.

答案： 【解析】：
由图可知，$a$在$-1$的左侧，所以$a \lt -1 \lt 0$，$b$在$1$的右侧，所以$b \gt 1 \gt 0$。
根据绝对值的定义，负数的绝对值是其相反数，正数的绝对值是其本身，所以$|a| \gt 0$，且$|a|=-a$（因为$a$是负数）。
由于$a \lt -1$，那么$-a \gt 1$，即$|a| \gt 1$。
$b \gt 1$，$1$就是$1$本身。
综合以上三点，可以得出$1\lt |a| \lt b$。
【答案】：$1\lt |a| \lt b$。

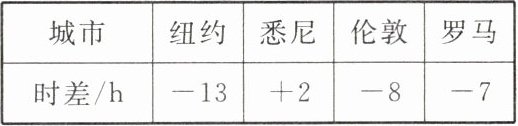
5. 下面的五个时钟显示了同一时刻国外四个城市的时间和北京时间,根据下表给出的某时刻国外四个城市与北京的时差(正数表示同一时刻比北京时间早,负数表示同一时刻比北京时间晚),可以判断城市C代表北京.(在A,B,C,D,E中选一个填在横线上)

答案： 【解析】：
本题考查正负数的实际应用。
由表可知，同一时刻，悉尼的时间比北京时间早$2$小时，纽约的时间比北京时间晚$13$小时，伦敦的时间比北京时间晚$8$小时，罗马的时间比北京时间晚$7$小时。
再由图可知，五个时钟显示的时间中，城市$C$与城市$E$的时间相差$2$小时，城市$C$与城市$A$的时间相差$13$小时，城市$C$与城市$D$的时间相差$7$小时，城市$C$与城市$B$的时间相差$8$小时。
所以，城市$C$代表北京。
【答案】：$C$

6. 如图所示,周长为6个单位长度的圆上的六等分点分别为$A$,$B$,$C$,$D$,$E$,$F$,点$A$落在1的位置. 若将圆在数轴上沿正方向滚动,则落在数轴上2025位置的点是C.

答案： 解：圆周长为6个单位长度，六等分点依次为A,B,C,D,E,F，滚动时每移动1个单位长度，下一个点与数轴位置对应。
点A在1的位置，向右滚动：
1位置：A
2位置：B
3位置：C
4位置：D
5位置：E
6位置：F
7位置：A（滚动一周回到A）
规律：位置数n与点的对应关系为(n-1)÷6的余数：
余数0→A，1→B，2→C，3→D，4→E，5→F
2025位置：(2025-1)=2024
2024÷6=337……2（余数为2）
余数2对应点C。
答案：C

7. 把下列各数的序号分别填在相应的集合里：
①$-5$；②$-\frac{4}{5}$；③2025；④$-(-4)$；⑤$\frac{22}{7}$；⑥$-|-13|$；⑦$-0.36$；⑧0；⑨$-0.\dot{6}$；⑩5%.
(1)正有理数集合：{③,④,⑤,⑩…}；
(2)负有理数集合：{①,②,⑥,⑦,⑨…}.

答案：
(1)正有理数集合：{③,④,⑤,⑩…}；
(2)负有理数集合：{①,②,⑥,⑦,⑨…}.

8. 如图所示,数轴上每一小段的单位长度为1,点$A$,$B$,$C$,$D在数轴上对应的数分别为a$,$b$,$c$,$d$.

(1)如果$a与d$互为相反数,那么$c= $-1.
(2)如果$|b| ＞ |d|$,那么$c$＜0；(填“＞”或“＜”)$a$,$b$,$c$,$d$中,可能互为相反数的是b和d（答案不唯一）.

答案：
(1)解：由数轴可知，点A与点D之间有8个单位长度，设点A表示的数为a，则点D表示的数为d=a+8。因为a与d互为相反数，所以a+d=0，即a+(a+8)=0，2a+8=0，2a=-8，a=-4。则点A表示-4，点B在点A右侧2个单位长度，所以b=-4+2=-2；点C在点B右侧1个单位长度，所以c=-2+1=-1。
(2)解：由数轴可知，点B在原点左侧，点D在原点右侧，设原点为O。若|b|＞|d|，则点B到原点的距离大于点D到原点的距离，所以原点在点C右侧，故c＜0。a、b、c、d中，可能互为相反数的是b和d（答案不唯一，合理即可）。
(1)-1
(2)＜；b和d（答案不唯一）