《2025年作业本江西教育出版社七年级数学上册人教版》

1. 计算:$(-2×3)^{2}÷9= $4.

答案： 解：$(-2×3)^{2}÷9$
$=(-6)^{2}÷9$
$=36÷9$
$=4$

2. 下列四个式子中,计算结果最小的是______(填序号).
①$-1^{3}+(-2)^{2}$;②$-1^{3}-(-2)^{2}$;③$-1^{3}×(-2)^{2}$;④$-1^{3}÷(-2)^{2}$.②

答案： 【解析】：
本题主要考查有理数的混合运算，包括乘方、加减法和乘除法。
需要分别计算四个式子的结果，然后比较大小，找出计算结果最小的式子。
① 对于式子 $-1^{3}+(-2)^{2}$：
首先计算乘方：
$-1^{3} = -1$
$(-2)^{2} = 4$
然后进行加法运算：
$-1 + 4 = 3$
② 对于式子 $-1^{3}-(-2)^{2}$：
首先计算乘方：
$-1^{3} = -1$
$(-2)^{2} = 4$
然后进行减法运算：
$-1 - 4 = -5$
③ 对于式子 $-1^{3}×(-2)^{2}$：
首先计算乘方：
$-1^{3} = -1$
$(-2)^{2} = 4$
然后进行乘法运算：
$-1 × 4 = -4$
④ 对于式子 $-1^{3}÷(-2)^{2}$：
首先计算乘方：
$-1^{3} = -1$，
$(-2)^{2} = 4$，
然后进行除法运算：
$-1 ÷ 4 = -\frac{1}{4}$，
最后，比较四个式子的结果：
$3 ＞ -\frac{1}{4} ＞ -4 ＞ -5$，
因此，计算结果最小的式子是②，结果为-5。
【答案】：②。

3. 如图所示,一只蚂蚁从点 A 沿数轴向左爬 3 个单位长度到达点 B. 若点 A 表示-1,设点 B 所表示的数为 m,则$|m-3|+(m+3)^{2025}=$6.

答案： 解：因为蚂蚁从点A沿数轴向左爬3个单位长度到达点B，点A表示-1，所以点B表示的数$m = -1 - 3 = -4$。
则$|m - 3| + (m + 3)^{2025} = |-4 - 3| + (-4 + 3)^{2025} = |-7| + (-1)^{2025} = 7 + (-1) = 6$。
6

4. 观察下面“品”字形中各数之间的规律,根据观察到的规律得出 a 的值为______.

答案： 【解析】：
观察“品”字形数阵，可发现以下规律：
对于每一组上下两个数，上面的数是从$1$开始的连续奇数，下面的两个数中，左边的数是从$2$开始的连续偶数，右边的数等于上面那个数与下面左边那个数的和。
第一组：上面数是$1$（第一个奇数），下面左边数是$2$（第一个偶数），下面右边数$3 = 1+2$。
第二组：上面数是$3$（第二个奇数），下面左边数是$4$（第二个偶数），下面右边数$7 = 3 + 4$。
第三组：上面数是$5$（第三个奇数），下面左边数是$8$（第三个偶数），下面右边数$13 = 5+8$。
以此类推，要求$a$的值，需要先确定$b$的值，再根据规律求出$a$。
观察上面数的规律，是从$1$开始的连续奇数，可表示为$2n - 1$（$n$为正整数），到$11$时，$2n - 1 = 11$，解得$n = 6$，说明$11$是第$6$个奇数。
观察下面左边数的规律，是从$2$开始的连续偶数，可表示为$2n$（$n$为正整数），当$n = 6$时，下面左边的数$b = 2×6 = 2^{6}=64$。
根据规律，下面右边的数$a$等于上面的数$11$与下面左边的数$b = 2^{6}=64$的和，即$a = 11 + 2^{6}=11 + 64 = 75$。
【答案】：$75$。

5. 计算.
(1)$(\frac{1}{2}-\frac{1}{3})×(-2)^{2}×(-6)$;
(2)$(-3^{2}+3)×5-(-2)^{3}÷4$;
(3)$-1^{4}-[2-(-3)^{2}]+|-8|÷(-4)$;
(4)$(-4)^{2}-1\frac{1}{2}×\frac{2}{9}-6÷(-\frac{2}{3})^{2}-(-2^{2})$.

答案：
(1)解：原式$=(\frac{3}{6}-\frac{2}{6})×4×(-6)$
$=\frac{1}{6}×4×(-6)$
$=\frac{1}{6}×(-24)$
$=-4$
(2)解：原式$=(-9 + 3)×5 - (-8)÷4$
$=(-6)×5 - (-2)$
$=-30 + 2$
$=-28$
(3)解：原式$=-1 - [2 - 9] + 8÷(-4)$
$=-1 - (-7) + (-2)$
$=-1 + 7 - 2$
$=4$
(4)解：原式$=16 - \frac{3}{2}×\frac{2}{9} - 6÷\frac{4}{9} - (-4)$
$=16 - \frac{1}{3} - 6×\frac{9}{4} + 4$
$=16 - \frac{1}{3} - \frac{27}{2} + 4$
$=20 - \frac{2}{6} - \frac{81}{6}$
$=20 - \frac{83}{6}$
$=\frac{120}{6} - \frac{83}{6}$
$=\frac{37}{6}$

6. 定义一种新运算“☆”,规定:$m☆n= m^{n}+mn-n$,例如:$2☆3= 2^{3}+2×3-3= 11$. 据此解答下列问题:
(1)求$(-2)☆4$的值;
(2)求$(-1)☆[(-5)☆2]$的值.

答案： 【解析】：
本题主要考查了新定义运算及有理数的混合运算，需要根据新定义运算规则，将给定的数值代入公式进行计算。
(1) 对于$(-2)☆4$，根据定义有：
$(-2)☆4 = (-2)^{4} + (-2) × 4 - 4$
$= 16 - 8 - 4$
$= 4$
(2) 对于$(-1)☆[(-5)☆2]$，首先需要计算内层的$(-5)☆2$：
$(-5)☆2 = (-5)^{2} + (-5) × 2 - 2$
$= 25 - 10 - 2$
$= 13$
然后再将结果代入外层的运算：
$(-1)☆13 = (-1)^{13} + (-1) × 13 - 13$
$= -1 - 13 - 13$
$= -27$
【答案】：
(1) $4$
(2) $-27$

7. 数学课上,老师用 A,B,C,D 四张圆形卡片分别代表一种运算,并依据这四张圆形卡片设计了数学游戏,学生可以将卡片 A,B,C,D 重新排序,进行一次列式计算. 例如,若按 A→B→C→D 的顺序进行运算,则可列算式为$[(+3)×(-3)-2]^{2}$. 当卡片 B 或 D 排在第一张时,可以选择任意一个有理数进行卡片 B 或 D 的运算,然后再将剩余卡片继续运算. 例如,若选择 4,并按 D→A→B→C 的顺序进行运算,则可列算式为$(4^{2}+3)×(-3)-2$.

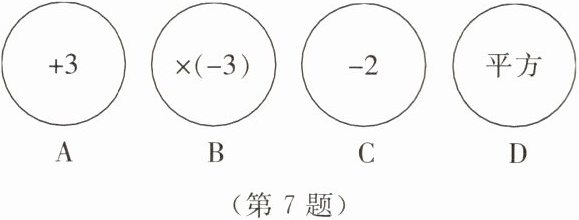
(1)算式$[(+3)×(-3)-2]^{2}$的结果为______,算式$(4^{2}+3)×(-3)-2$的结果为______.
(2)若甲同学选择了 A→C→B→D 的顺序进行运算,则他列式计算的结果为______.
(3)乙同学选了-5,并按 D→(______)→(______)的顺序运算. 若乙同学列式计算的结果刚好为-66,求乙同学选择的运算顺序.
(1)121；-59
(2)9
(3)A；B

答案：

###
(1)

- 计算\([(+3)×(-3)-2]^{2}\)：

  先算括号内的乘法：\((+3)×(-3)= -9\)；

  再算括号内的减法：\(-9 - 2 = -11\)；

  最后算平方：\((-11)^{2}=121\)。

- 计算\((4^{2}+3)×(-3)-2\)：

  先算平方：\(4^{2}=16\)；

  再算括号内的加法：\(16 + 3 = 19\)；

  然后算乘法：\(19×(-3)= -57\)；

  最后算减法：\(-57 - 2 = -59\)。

###
(2)

甲同学按\(A→C→B→D\)的顺序运算，列式为\([(+3)-2]×(-3)\)的平方，即\([(3 - 2)×(-3)]^{2}\)。

  先算小括号：\(3 - 2 = 1\)；

  再算中括号：\(1×(-3)= -3\)；

  最后算平方：\((-3)^{2}=9\)。

###
(3)

设乙同学的运算顺序为\(D→C→X→Y\)（\(X\)、\(Y\)为\(A\)或\(B\)），已知选了\(-5\)，结果为\(-66\)。

  - 先算\(D\)：\((-5)^{2}=25\)；

  - 再算\(C\)：\(25 - 2 = 23\)；

  接下来分情况：

    - 若下一个是\(A\)（即\(+3\)）：\(23 + 3 = 26\)，再算\(B\)（\(×(-3)\)）：\(26×(-3)= -78\neq -66\)，不符合。

    - 若下一个是\(B\)（即\(×(-3)\)）：\(23×(-3)= -69\)，再算\(A\)（\(+3\)）：\(-69 + 3 = -66\)，符合。

  所以乙同学选择的运算顺序是\(D→C→B→A\)。

综上，答案依次为：
(1)\(\boxed{121}\)，\(\boxed{-59}\)；
(2)\(\boxed{9}\)；
(3)\(\boxed{B}\)，\(\boxed{A}\)，运算顺序为\(D→C→B→A\)。