《2025年作业本江西教育出版社七年级数学上册人教版》

1. 用代数式表示“$a的3倍与b$的差”是$3a - b$.

答案： 【解析】：
题目要求用代数式表示“$a$的3倍与$b$的差”。首先，我们需要理解题目中的“3倍”和“差”的含义。
“3倍”即乘以3，所以$a$的3倍可以表示为$3a$。
“差”即两数相减，所以$a$的3倍与$b$的差可以表示为$3a - b$。
【答案】：
$3a - b$

2. 已知一件羽绒服的标价为$a$元,现按标价打八五折出售,则现在的售价为0.85a元(用含$a$的代数式表示).

答案： 解：按标价打八五折出售，即按标价的85%出售。
售价 = 标价 × 85% = $ a × 85\% = 0.85a $
故现在的售价为 $ 0.85a $ 元。
$0.85a$

3. 某同学到文具商店为学校美术组的$20$名同学购买铅笔和橡皮. 已知铅笔每支$m$元,橡皮每块$n$元,若给每名同学买$3支铅笔和2$块橡皮,则一共需付款$(60m + 40n)$元(用含$m$,$n$的代数式表示).

答案： 【解析】：
本题主要考查利用代数式表示实际问题中的数量关系。
首先，计算每名同学所需支付的金额。每名同学买3支铅笔和2块橡皮，所以每名同学需要支付$3m + 2n$元。
然后，由于有20名同学，所以总付款金额为$20 × (3m + 2n)$元。
进一步化简，得到总付款金额为$(60m + 40n)$元。
【答案】：
$(60m + 40n)$

4. 下列问题中的两个变量之间的关系,其中是反比例关系的是______(填序号).
①长为$100m的绳子剪下m\ m$后,还剩下$n\ m$；②买单价为$10元的笔记本x$本,一共用了$y$元；③矩形的面积为$24cm^2$,相邻两边的边长分别是$x\ cm$,$y\ cm$；④家到学校的距离为$480m$,小明步行上学的平均速度为$v\ m/min$,所用时间为$t\ min$.
③④

答案： 【解析】：
本题主要考察反比例关系的定义和识别。反比例关系是指两个变量之间的一种关系，当其中一个变量增大时，另一个变量会相应地减小，而它们的乘积保持为一个常数。
① 对于长为$100m$的绳子剪下$m \ m$后，还剩下$n \ m$，有 $n = 100 - m$，这是一个一次函数关系，不是反比例关系。
② 对于买单价为$10$元的笔记本$x$本，一共用了$y$元，有 $y = 10x$，这是一个正比例关系，不是反比例关系。
③ 对于矩形的面积为$24 \ cm^2$，相邻两边的边长分别是$x \ cm$，$y \ cm$，有 $xy = 24$，这是一个反比例关系，因为$x$和$y$的乘积是一个常数。
④ 对于家到学校的距离为$480 \ m$，小明步行上学的平均速度为$v \ m/min$，所用时间为$t \ min$，有 $vt = 480$，这也是一个反比例关系，因为$v$和$t$的乘积是一个常数。
所以，满足反比例关系的是③和④。
【答案】：
③④

5. 小明在爬山时,第一阶段的平均速度为$v\ m/min$,所用时间为$m\ min$；第二阶段的平均速度为$\frac{1}{2}v\ m/min$,所用时间为$n\ min$.
(1)第一阶段的路程为$vm$$m$；第二阶段的路程为$\frac{1}{2}vn$$m$.(均用含$v$,$m或n$的代数式表示)
(2)已知小明上山的路程和下山的路程相同,下山时,小明的平均速度保持为$2v\ m/min$,那么小明下山用了多长时间？
小明上山走的总路程为$vm + \frac{1}{2}vn$，
下山时，小明的平均速度保持为$2v\ m/min$，
则小明下山用的时间为：
$\frac{vm + \frac{1}{2}vn}{2v}$
= $\frac{2vm + vn}{4v}$
= $\frac{m}{2} + \frac{n}{4}\ (min)$

答案： 【解析】：
本题主要考查代数式的应用和速度、时间、路程之间的关系。
(1) 第一阶段的路程可以通过速度乘以时间来计算，即 $v × m$。
第二阶段的路程同样可以通过速度乘以时间来计算，但第二阶段的速度是第一阶段速度的一半，即 $\frac{1}{2}v$，时间为 $n$，所以第二阶段的路程为 $\frac{1}{2}v × n$。
(2) 下山时，小明的平均速度保持为 $2v\ m/min$。
首先，需要计算小明上山的总路程，这可以通过将第一阶段和第二阶段的路程相加来得到，即 $vm + \frac{1}{2}vn$。
然后，用这个总路程除以下山时的平均速度 $2v$，就可以得到小明下山所用的时间。
【答案】：
(1) 第一阶段的路程为 $vm\ m$；第二阶段的路程为 $\frac{1}{2}vn\ m$。
(2) 小明上山走的总路程为 $vm + \frac{1}{2}vn$，
下山时，小明的平均速度保持为 $2v\ m/min$，
则小明下山用的时间为：
$\frac{vm + \frac{1}{2}vn}{2v}$
= $\frac{2vm + vn}{4v}$
= $\frac{m}{2} + \frac{n}{4}\ (min)$

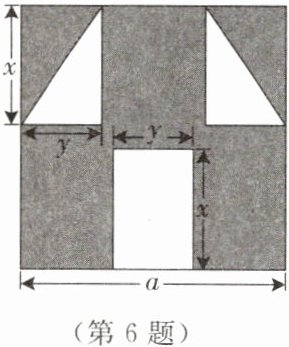
6. “囧”像一个人脸郁闷的神情. 如图所示,边长为$a$的正方形纸片,剪去两个一样的小直角三角形和一个小长方形后得到一个“囧”字图案. 设剪去的两个小直角三角形的两直角边长分别为$x$,$y$,剪去的小长方形的长和宽也分别为$x$,$y$.
(1)用式子表示“囧”字图案的面积$S$(用含$a$,$x$,$y$的式子表示).
(2)当$a = 20$,$x = 5$,$y = 4$时,求$S$的值.

答案： 【解析】：本题主要考查列代数式以及代数式求值的知识点。
(1)首先，计算正方形的面积，即$a^2$。
然后，计算两个小直角三角形的面积，每个三角形的面积为$\frac{1}{2}xy$，两个三角形的面积总和为$2 × \frac{1}{2}xy = xy$。
接着，计算小长方形的面积，即$xy$。
最后，用正方形的面积减去两个小直角三角形的面积和小长方形的面积，得到“囧”字图案的面积$S$，即$S = a^2 - xy-xy = a^2 - 2xy$。
(2)将$a = 20$，$x = 5$，$y = 4$代入$S =a^2 - 2xy$中，得到$S = 20^2 - 2 × 5 × 4 = 400 - 40 = 360$。
【答案】：（1）$S=a^2 - 2xy$；（2）$S=360$