《2025年作业本江西教育出版社七年级数学上册人教版》

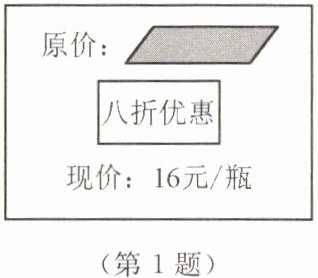
1. 超市里某种洗发水的价格标签如图所示,该种洗发水的原价是20元/瓶.

答案： 【解析】：本题可根据现价与原价的关系，结合一元一次方程来求解洗发水的原价。
已知洗发水打八折优惠后的现价为$16$元/瓶，设该种洗发水的原价是$x$元/瓶。
打八折即现价是原价的$80\%$，可据此列出方程$0.8x = 16$，求解该方程即可得到原价。
【答案】：解：设该种洗发水的原价是$x$元/瓶。
由题意得$0.8x = 16$，
两边同时除以$0.8$，$x=\frac{16}{0.8}=20$。
故答案为$20$。

2. 某商品现在售价是32元,比原来售价降低了60%,则原来售价是80元.

答案： 解：设原来售价是$x$元。
根据题意，现在售价比原来降低了$60\%$，则现在售价是原来售价的$(1 - 60\%)$，可列方程：
$(1 - 60\%)x = 32$
$0.4x = 32$
$x = 32÷0.4$
$x = 80$
答：原来售价是$80$元。

3. 一件商品进价是40元,标价是60元,为了促销,按标价八折优惠销售,则该商品的利润率为______20%.

答案： 解：售价为 $60 × 0.8 = 48$ 元
利润为 $48 - 40 = 8$ 元
利润率为 $\frac{8}{40} × 100\% = 20\%$
20%

4. 超市店庆促销,某种书包原价每个x元,第一次降至九折,第二次降价每个又减10元,经两次降价后售价为每个80元,则可列方程为______0.9x - 10 = 80.

答案： 解：书包原价每个$x$元，第一次降至九折，此时价格为$0.9x$元。
第二次降价每个又减10元，所以第二次降价后的售价为$(0.9x - 10)$元。
已知经两次降价后售价为每个80元，因此可列方程为：$0.9x - 10 = 80$。
故答案为：$0.9x - 10 = 80$。

5. 某人将甲、乙两种股票同时卖出,其中甲种股票市值1200元,赢利20%；乙种股票市值也是1200元,但亏损20%.他此次交易结果是赢利还是亏损？

答案： 【解析】：
本题主要考察一元一次方程在实际问题中的应用，特别是涉及到赢利和亏损的计算。
首先，我们需要计算出甲、乙两种股票的原价，然后根据原价和卖出的价格来计算赢利或亏损的总额。
对于甲种股票，原价设为$x$元，由于赢利了$20\%$，所以卖出价格为$x(1+20\%)=1200$元，解这个方程可以得到甲种股票的原价。
对于乙种股票，原价设为$y$元，由于亏损了$20\%$，所以卖出价格为$y(1-20\%)=1200$元，解这个方程可以得到乙种股票的原价。
最后，我们可以计算出总的赢利或亏损情况，即（甲股票原价+乙股票原价）与（甲股票卖出价+乙股票卖出价）的差。
【答案】：
解：设甲种股票的原价为$x$元，
根据赢利情况，我们有方程：$x(1 + 20\%) = 1200$，
解这个方程，我们得到：$x = \frac{1200}{1.2} = 1000$元，
所以，甲种股票赢利了$1200 - 1000 = 200$元。
设乙种股票的原价为$y$元，
根据亏损情况，我们有方程：$y(1 - 20\%) = 1200$，
解这个方程，我们得到：$y = \frac{1200}{0.8} = 1500$元，
所以，乙种股票亏损了$1500 - 1200 = 300$元。
总的赢利或亏损情况为：$200 - 300 = -100$元，
即这次交易他亏损了$100$元。

6. 七年级(1)班开展了一次“中华优秀传统文化”知识竞赛,共设20道分值相同的选择题,每题必答.下表中记录了若干名参赛选手的竞赛得分情况.

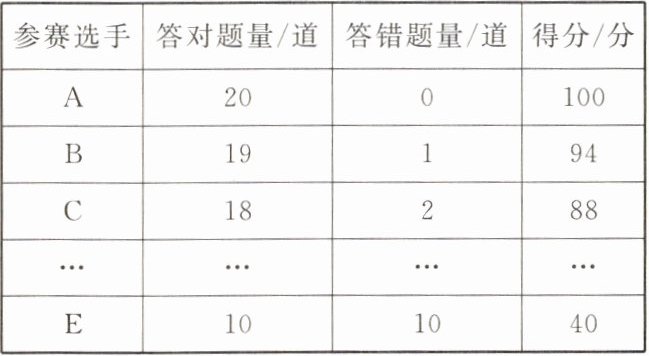
(1)某选手答对17题,可得82分.
(2)观察表中数据：得分规则是什么？答对一题得5分，答错一题扣1分
(3)用方程知识解答：若选手F得64分,则他答对了几道题？14
(4)参赛选手G说他得78分,可能吗？为什么？不可能，理由：设他答对了y道题，则答错了(20 - y)道题，根据得分规则可列方程5y - (20 - y) = 78，解得y = 49/3，y不是整数，所以不可能。

答案： 【解析】：
（1）观察给出的数据，可以发现答对一题得5分，答错一题扣1分。
这是因为选手A答对20题得100分，即$20 × 5 = 100$；
选手B答对19题，答错1题，得分为$19 × 5 - 1 = 94$，以此类推。
因此，答对17题，答错3题的得分为$17 × 5 - 3 = 82$，
综上，本题的答案为：82；
（2）得分规则是：答对一题得5分，答错一题扣1分；
（3）设他答对了$x$道题，则他答错了$(20 - x)$道题。
根据得分规则，可以列出方程：
$5x - (20 - x) = 64$，
解这个方程，得到：
$5x - 20 + x = 64$，
$6x = 84$，
$x = 14$，
综上，若选手F得64分，则他答对了14道题；
（4）假设他得78分可能，设他答对了$y$道题，则他答错了$(20 - y)$道题。
根据得分规则，可以列出方程：
$5y - (20 - y) = 78$，
解这个方程，得到：
$5y - 20 + y = 78$，
$6y = 98$，
$y = \frac{49}{3}$，
因为$y$必须是整数（因为题数不能是小数），所以$\frac{49}{3}$不满足条件。
因此，参赛选手G说他得78分是不可能的。
【答案】：
（1）82；
（2）答对一题得5分，答错一题扣1分；
（3）14；
（4）不可能，理由见上述解析。