《2025年初中必刷题九年级数学上册北师大版》

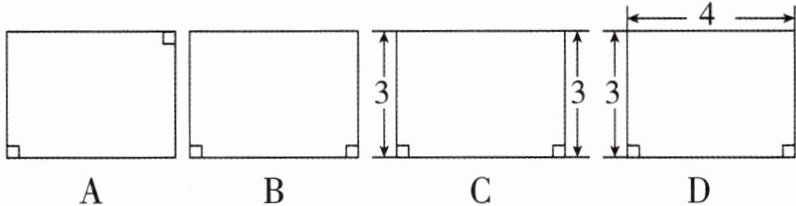
1[2024浙江台州调研]下列图形一定为矩形的是( )

答案： C 【解析】A有两个角是直角的四边形不一定是矩形，故A不符合题意；B有两个角是直角的四边形不一定是矩形，故B不符合题意；C由两个角是直角得出一组对边平行，且这组对边相等，是平行四边形，又由有一个角是直角得是矩形，故C符合题意；D有两个角是直角的四边形不一定是矩形，故D不符合题意。

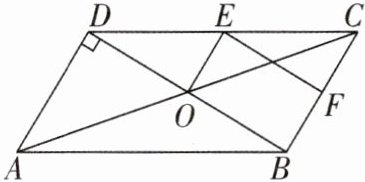
2[2025陕西咸阳质检]如图,在$□ ABCD$中,对角线AC,BD相交于点O,$AD⊥DB$,点E,F分别是CD,BC的中点,连接OE,EF.求证:四边形OEFB是矩形.

答案： 【证明】
∵ 点E,F分别是CD,BC的中点，
∴ EF//BD,EF=$\frac{1}{2}$BD。
∵ 在$□ ABCD$中，OB=$\frac{1}{2}$BD，
∴ EF//OB,EF=OB，
∴ 四边形OEFB是平行四边形。
∵ AD//BC,AD⊥DB，
∴ BC⊥BD，
∴ ∠OBF=90°，
∴ $□ OEFB$是矩形。

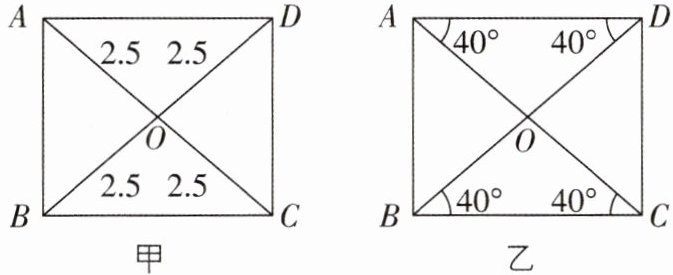
3[2025河北邢台质检]如图,有甲、乙两个四边形,分别标出了部分数据,则下列判断正确的是( )


A.甲是矩形
B.乙是矩形
C.甲、乙均是矩形
D.甲、乙都不是矩形

答案： A 【解析】由题意知，甲四边形中对角线相等且互相平分，
∴ 甲四边形是矩形。在乙四边形中，由题意易得OA=OD,OB=OC，而OA，OB的数量关系未知，
∴ 乙四边形不一定是矩形。故选A。

4[2025安徽宿州质检]甲、乙、丙、丁四位同学到木工厂参观时,木工师傅让他们用尺子帮助检测一个窗框是否为矩形,他们各自做了如下检测:
甲:量得窗框两组对边分别相等;
乙:量得窗框对角线相等;
丙:量得窗框的一组邻边相等:
丁:量得窗框的两组对边分别相等且两条对角线相等.
检测后,他们都判断该窗框是矩形,则检测方法正确的同学是____.

答案： 丁 【解析】根据两组对边分别相等的四边形是平行四边形，对角线相等的平行四边形是矩形可知，丁的检测方法正确，故答案为丁。

5[2024重庆沙坪坝区调研]如图,将$□ ABCD$的边AB延长至点E,使$BE= AB$,连接DE,EC,BD,DE交BC于点O.
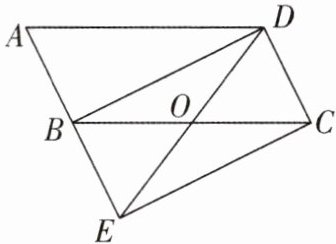
(1)求证:$\triangle ABD\cong \triangle BEC;$
(2)若$∠BOD= 2∠A$,求证:四边形BECD是矩形.

答案： 【证明】
(1)在平行四边形ABCD中，AD=BC，AB=CD,AB//CD，则BE//CD。又
∵ AB=BE，
∴ BE=DC，
∴ 四边形BECD为平行四边形，
∴ BD=EC。在△ABD与△BEC中，$\left\{\begin{array}{l} AB=BE,\\ BD=EC,\\ AD=BC,\end{array}\right.$
∴ $\triangle ABD\cong \triangle BEC(SSS)$。
(2)由
(1)知，四边形BECD为平行四边形，则OD=OE,OC=OB。
∵ 四边形ABCD为平行四边形，
∴ ∠A=∠BCD。又
∵ ∠BOD=2∠A,∠BOD=∠OCD+∠ODC，
∴ ∠OCD=∠ODC，
∴ OC=OD，
∴ OC+OB=OD+OE，即BC=ED，
∴ 平行四边形BECD为矩形。

6[2024陕西西安调研]如图,在矩形ABCD中,M为AD边的中点,P为BC上一点,$PE⊥MC,PF⊥MB$,当AB,BC满足条件____时,四边形PEMF为矩形.

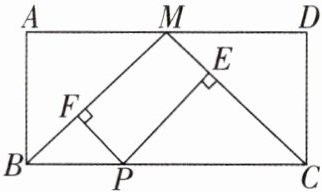
答案： AB=$\frac{1}{2}$BC 【解析】当AB=$\frac{1}{2}$BC时，四边形PEMF是矩形。
∵ 在矩形ABCD中，M为AD边的中点，AB=$\frac{1}{2}$BC，
∴ AB=DC=AM=MD，∠A=∠D=90°，
∴ ∠AMB=∠DMC=45°，
∴ ∠BMC=90°。又
∵ PE⊥MC,PF⊥MB，
∴ ∠PFM=∠PEM=90°，
∴ 四边形PEMF是矩形。故答案为AB=$\frac{1}{2}$BC。

7[2025山东济南期中]如图,在$□ ABCD$中,$CE⊥AB,AF⊥CD$,垂足分别为E,F,求证:四边形AECF是矩形.

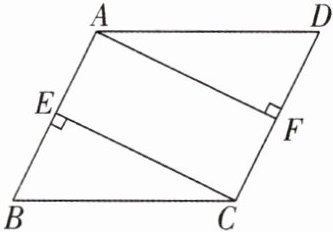
答案： 【证明】
∵ CE⊥AB,AF⊥CD，
∴ ∠AEC=∠AFC=∠AFD=90°。
∵ 四边形ABCD是平行四边形，
∴ AB//CD，
∴ ∠FAE=∠AFD=90°，
∴ ∠AEC=∠AFC=∠FAE=90°，
∴ 四边形AECF是矩形。