《2025年初中必刷题九年级数学上册北师大版》

1 [中]已知方程 $ x^{2}-6x + 4= □ $,等号右侧的数字印刷不清楚.若可以将其配方成 $ (x - p)^{2}= 7 $ 的形式,则印刷不清楚的数字是( )

A.6
B.9
C.2
D.-2

答案： C 【解析】设印刷不清楚的数字是a.
∵(x-p)²=x²-2px+p²=7，
∴x²-2px=7-p²，
∴x²-2px+4=11-p².
∵方程x²-6x+4=□，等号右侧的数字印刷不清楚，且可以将其配方成(x-p)²=7的形式，
∴-2p=-6，a=11-p²，
∴p=3，a=11-3²=2，即印刷不清楚的数字是2，故选 C.

2 新考法 [2024 江苏泰州姜堰区期中,中]欧几里得的《几何原本》中记载了形如 $ x^{2}-2bx + 4c^{2}= 0(b ＞ 2c ＞ 0) $ 的方程的图形解法:如图,画 $ Rt\triangle ABC $,使 $ ∠ACB = 90^{\circ},AC = 2c,AB = b $,以 $ B $ 为圆心, $ BC $ 长为半径画圆,交射线 $ AB $ 于点 $ D,E $,则该方程较大的根是( )


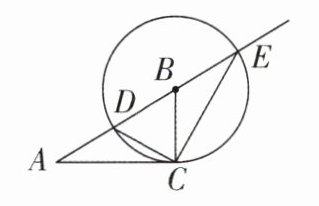
A.$ CE $ 的长度
B.$ CD $ 的长度
C.$ DE $ 的长度
D.$ AE $ 的长度

答案： D 【解析】
∵x²-2bx+4c²=0，
∴x²-2bx=-4c²，
∴x²-2bx+b²=b²-4c²，即(x-b)²=b²-4c²，
∴x-b=±√(b²-4c²)，
∴x₁=b+√(b²-4c²)，x₂=b-√(b²-4c²). 在Rt△ABC中，∠ACB=90°，AC=2c，AB=b，
∴BC=√(AB²-AC²)=√(b²-4c²)，
∴方程较大的根为AB+BC=AB+BE=AE的长度，故选 D.

3 [中]若方程 $ x^{2}+4x - 16= 0 $ 能配方成 $ (x + p)^{2}+q = 0 $ 的形式,则直线 $ y = px + q $ 不经过的象限是______。

答案： 第二象限 【解析】x²+4x-16=0，x²+4x=16，x²+4x+4=20，(x+2)²=20，即(x+2)²-20=0，所以p=2，q=-20，直线表达式为y=2x-20，此直线经过第一、三、四象限，不经过第二象限. 故答案为第二象限.

4 [2024 河南驻马店期末,中]对于两个互不相等的实数 $ p,q $,我们用符号 $ min\{p,q\} $ 表示 $ p,q $ 两数中较小的数,如 $ min\{1,2\}= 1 $,若 $ min\{(x - 1)^{2},x^{2}\}= 1 $,则 $ x = $______。

答案： 2或-1
思路分析 min{(x-1)²,x²}=1⇒{(x-1)²=1,(x-1)²＜x², x²=1,x²＜(x-1)².
【解析】当(x-1)²＜x²，即x＞1/2时，方程为(x-1)²=1，开方得x-1=1或x-1=-1，解得x=0（舍去）或x=2；当(x-1)²＞x²，即x＜1/2时，方程为x²=1，开方得x=-1或x=1（舍去）. 故答案为2或-1.

5 [2025 山东滨州校级质检,中]观察下列方程及其解的特征:
① $ x+\frac{1}{x}= 2 $ 的解为 $ x_{1}= x_{2}= 1 $;
② $ x+\frac{1}{x}= \frac{5}{2} $ 的解为 $ x_{1}= 2,x_{2}= \frac{1}{2} $;
③ $ x+\frac{1}{x}= \frac{10}{3} $ 的解为 $ x_{1}= 3,x_{2}= \frac{1}{3} $;
…
解答下列问题:
(1)请猜想:方程 $ x+\frac{1}{x}= \frac{26}{5} $ 的解为______;
(2)请猜想:关于 $ x $ 的方程 $ x+\frac{1}{x}= $______的解为 $ x_{1}= a,x_{2}= \frac{1}{a}(a \neq 0) $;
(3)请以解方程 $ x+\frac{1}{x}= \frac{26}{5} $ 为例,验证(1)中猜想的结论的正确性.下面给出了验证的部分过程,请把剩余部分补充完整.
解:原方程可化为 $ x^{2}-\frac{26}{5}x= -1 $。

答案： 【解】
(1)观察可得题干所给方程及其解的特征为两个解互为倒数，且整数解与方程右边的分母相同，故猜想方程x+(1/x)=26/5的解为x₁=5，x₂=1/5. 故答案为x₁=5，x₂=1/5.
(2)
∵x+(1/x)=2的解为x₁=x₂=1，x+(1/x)=5/2的解为x₁=2，x₂=1/2，x+(1/x)=10/3的解为x₁=3，x₂=1/3，……，
∴x+(1/x)=(a²+1)/a的解为x₁=a，x₂=1/a（a≠0）. 故答案为(a²+1)/a.
(3)原方程可化为x²-(26/5)x=-1，
∴x²-(26/5)x+(-13/5)²=-1+(-13/5)²，
∴(x-13/5)²=144/25，
∴x-13/5=±12/5，
∴x₁=5，x₂=1/5.

6 核心素养运算能力 [2025 湖南衡阳期中,中]小明在解一元二次方程时,发现有这样一种解法:
如解方程 $ x(x + 4)= 6 $。
解:原方程可变形为 $[(x + 2)-2][(x + 2)+2]= 6,(x + 2)^{2}-2^{2}= 6,(x + 2)^{2}= 10 $。直接开平方并整理,得 $ x_{1}= -2+\sqrt{10},x_{2}= -2-\sqrt{10} $。
我们称小明这种解法为“平均数法”。
(1)下面是小明用“平均数法”解方程 $ (x + 5)\cdot(x + 9)= 5 $ 时写的解题过程。
解:原方程可变形为 $[(x + a)-b][(x + a)+b]= 5,(x + a)^{2}-b^{2}= 5,\therefore(x + a)^{2}= 5 + b^{2} $。直接开平方并整理,得 $ x_{1}= c,x_{2}= d(c ＞ d) $。
上述过程中的 $ a,b,c,d $ 表示的数分别为______,______,______,______。
(2)请用“平均数法”解方程: $ (x - 5)(x + 7)= 12 $。

答案： 【解】
(1)
∵(x+5)(x+9)=5，
∴[(x+7)-2][(x+7)+2]=5，
∴(x+7)²-2²=5，
∴(x+7)²=9，
∴x+7=3或x+7=-3，解得x₁=-4，x₂=-10，
∴题中a，b，c，d表示的数分别为7，2，-4，-10. 故答案为7，2,-4,-10.
(2)
∵(x-5)(x+7)=12，
∴[(x+1)-6][(x+1)+6]=12，
∴(x+1)²-36=12，
∴(x+1)²=48，
∴x+1=4√3或x+1=-4√3，解得x₁=-1+4√3，x₂=-1-4√3.