《2025年初中必刷题九年级数学上册北师大版》

1 [2025 河北雄安新区质检,中]用尺规作图的方法在一个平行四边形内作菱形 ABCD,下列作法错误的是 ( )

答案： A 【解析】A 由作法得 $\angle DAB=\angle BCD$. 因为 $AD// BC$，所以 $\angle DAB+\angle ABC=180^\circ$，所以 $\angle BCD+\angle ABC=180^\circ$，所以 $AB// CD$，则四边形 ABCD 为平行四边形 符合题意 B 由作法得 $\angle BAC=\angle DAC$, $\angle DCA=\angle BCA$，则 $\triangle ADC\cong \triangle ABC$，所以 $AB=AD$, $BC=CD$. 因为 $AD// BC$，所以 $\angle DAC=\angle BCA$，所以 $\angle BAC=\angle BCA$，所以 $AB=BC$，所以 $AB=BC=AD=CD$，则四边形 ABCD 为菱形 不符合题意 C 连接 AC，由作法得 $BA=BC$, $AD=AB=AC$，则 $\triangle ABC$ 为等边三角形，所以易知 $\triangle ACD$ 为等边三角形，所以 $AB=BC=CD=AD$，则四边形 ABCD 为菱形 不符合题意 D 由作法得 AC 垂直平分 BD，所以 $AB=AD$, $CB=CD$，则易得 $\triangle ABD\cong \triangle CBD$，所以 $BA=BC=CD=AD$，则四边形 ABCD 为菱形 不符合题意

2 [2025 湖北恩施州期末,中]如图,过□ABCD 的对角线 BD 的中点 O 作两条互相垂直的直线,分别交 AB,BC,CD,DA 于 E,F,G,H 四点,连接 EF,FG,GH,HE,下列结论正确的是$ ( )A. FH= AB B. S_{四边形EFGH}= \frac{1}{2}S_{四边形ABCD}C. FG= \frac{1}{2}BD D. $四边形 EFGH 是菱形

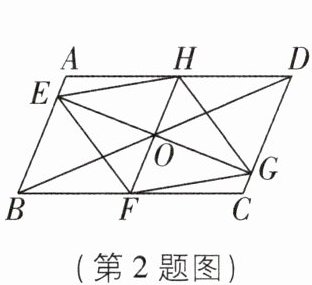
答案： D 【解析】
∵ E,F,G,H 不是定点，
∴ FH 不一定等于 AB，$S_{\text{四边形}EFGH}$ 不一定等于 $\frac{1}{2}S_{\text{四边形}ABCD}$，故选项 A、B 错误.
∵ F,G 不一定分别是 BC,CD 的中点，
∴ FG 不一定等于 $\frac{1}{2}BD$，故选项 C 错误.
∵ 四边形 ABCD 是平行四边形，
∴ $BO=OD$, $AD// CB$，
∴ $\angle HDO=\angle FBO$. 在 $\triangle HDO$ 和 $\triangle FBO$ 中，$\left\{\begin{array}{l} \angle HDO=\angle FBO,\\ DO=BO,\\ \angle HOD=\angle FOB,\end{array}\right.$
∴ $\triangle HDO\cong \triangle FBO$（ASA），
∴ $OH=OF$. 同理可得 $OE=OG$，
∴ 四边形 EFGH 是平行四边形. 又
∵ $HF\perp EG$，
∴ 平行四边形 EFGH 是菱形，故选项 D 正确. 故选 D.

3 [2025 江苏扬州质检,中]如图,在□ABCD 中,∠BAD 的平分线交线段 BC 于点 E,交线段 DC 的延长线于点 F,以 EC,CF 为邻边作□ECFG,若∠ABC= 120°,则∠BDG= ____.

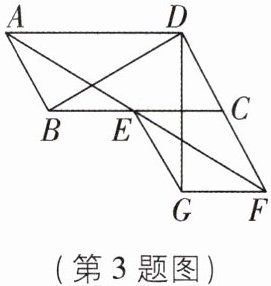
答案： $60^\circ$ 【解析】延长 AB,FG 交于 H，连接 HD.
∵ $AD// BC$, $BC// GF$，
∴ $AD// GF$.
∵ $AB// DF$，
∴ 四边形 AHFD,四边形 BCFH 为平行四边形. 对角线互相垂直的四边形的面积等于其对角线的乘积的一半. 在判定四边形是菱形时，容易错把对角线互相垂直的四边形当成菱形，如此题中，若想利用 $EG\perp FH$ 证明四边形 EFGH 为菱形，应先证其为平行四边形.
∵ $\angle ABC=120^\circ$，AF 平分 $\angle BAD$，
∴ $\angle DAF=\frac{1}{2}(180^\circ -120^\circ )=30^\circ$, $\angle ADC=120^\circ$，
∴ $\angle DFA=30^\circ$，
∴ $\angle DAF=\angle DFA$，
∴ $AD=DF$，
∴ 平行四边形 AHFD 为菱形，
∴ 易得 $\triangle ADH\cong \triangle FDH$，且均为等边三角形，
∴ $DH=DF$, $\angle BHD=\angle GFD=\angle HDG=60^\circ$.
∵ $AD// EC$，
∴ $\angle CEF=\angle DAF=\angle DFA=30^\circ$，
∴ $CE=CF$. 又
∵ 四边形 ECFG 为平行四边形，
∴ 四边形 ECFG 为菱形，
∴ $CE=CF=FG=EG$.
∵ 四边形 BCFH 为平行四边形，
∴ $BH=CF$，
∴ $BH=GF$. 在 $\triangle BHD$ 与 $\triangle GFD$ 中，$\left\{\begin{array}{l} DH=DF,\\ \angle BHD=\angle GFD,\\ BH=GF,\end{array}\right.$
∴ $\triangle BHD\cong \triangle GFD$（SAS），
∴ $\angle BDH=\angle GDF$，
∴ $\angle BDG=\angle BDH+\angle HDG=\angle GDF+\angle HDG=60^\circ$. 故答案为 $60^\circ$.

4 [2025 福建厦门校级期中改编,中]在学习了“菱形的性质与判定”后,小明根据所学的内容,试着定义了一个新的特殊四边形,规定:对角线互相垂直的四边形称为“垂美四边形”,如图(1)所示,AC⊥BD,则四边形 ABCD 为“垂美四边形”.
(1)【概念理解】证明:有三条边相等的“垂美四边形”是菱形(写出已知、求证);
(2)【性质探索】如图(1),若记“垂美四边形”ABCD 的面积为 S,求出 S 与 AC,BD 之间的关系;
(3)【性质应用】小明为了证明勾股定理,尝试将两个全等的直角三角形(Rt△ABC≌Rt△BED)按图(2)方式摆放,其中 B,C,E 在一条直线上,若假设直角三角形三边长为 x,y,z,即 BC= ED= x,AB= BE= y,AC= BD= z,试利用(2)中结论证明勾股定理.
]

答案：
(1)【解】已知：如图，四边形 ABCD 的两条对角线互相垂直，即 $AC\perp BD$，且 $AB=BC=CD$. 求证：四边形 ABCD 是菱形. 证明：
∵ $AC\perp BD$，
∴ $\angle BOA=\angle BOC=90^\circ$. 在 $Rt\triangle BOA$ 和 $Rt\triangle BOC$ 中，$\left\{\begin{array}{l} OB=OB,\\ AB=CB,\end{array}\right.$
∴ $Rt\triangle AOB\cong Rt\triangle COB$（HL），
∴ $OA=OC$. 同理可得 $Rt\triangle COD\cong Rt\triangle COB$（HL），
∴ $OD=OB$，
∴ 四边形 ABCD 是平行四边形.
∵ $AC\perp BD$，
∴ 四边形 ABCD 是菱形，
∴ 有三条边相等的“垂美四边形”是菱形.
(2)【解】在题图（1）中，
∵ $S_{\text{四边形}ABCD}=S_{\triangle ABC}+S_{\triangle ADC}=\frac{1}{2}AC\cdot BO+\frac{1}{2}AC\cdot DO=\frac{1}{2}AC\cdot BD$，
∴ $S=\frac{1}{2}AC\cdot BD$.
(3)【证明】连接 CD,AD. 由已知可得 $\angle BCA=\angle EDB$.
∵ $\angle CBO+\angle EDB=90^\circ$，
∴ $\angle CBO+\angle BCA=90^\circ$，
∴ $AC\perp BD$，
∴ 四边形 ABCD 是“垂美四边形”. 由（2）可得 $S_{\text{四边形}ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}z^{2}$.
∵ $\angle BED=\angle ABC=90^\circ$，
∴ 易知四边形 ABED 为直角梯形.
∵ $S_{\text{四边形}ABCD}=S_{\text{梯形}ABED}-S_{\triangle CED}=(x+y)× y× \frac{1}{2}-\frac{1}{2}× x× (y-x)=\frac{1}{2}y^{2}+\frac{1}{2}xy+\frac{1}{2}x^{2}-\frac{1}{2}xy=\frac{1}{2}y^{2}+\frac{1}{2}x^{2}$，
∴ $\frac{1}{2}z^{2}=\frac{1}{2}y^{2}+\frac{1}{2}x^{2}$，即 $z^{2}=y^{2}+x^{2}$，即勾股定理得证.

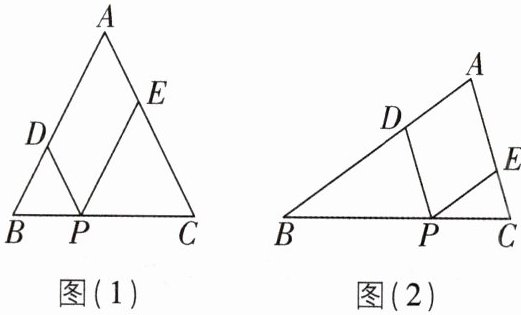
5 核心素养推理能力[2024 河南郑州调研,中]如图(1),△ABC 为等腰三角形,AB= AC= 6,P 点是底边 BC 上的一个动点,PD//AC,PE//AB,D,E 分别在 AB,AC 上.
(1)求四边形 ADPE 的周长.
(2)当点 P 运动到什么位置时,四边形 ADPE 是菱形? 并说明理由.
(3)如果△ABC 不是等腰三角形(如图(2)),其他条件不变,当点 P 运动到什么位置时,四边形 ADPE 是菱形? 并说明理由.
]

答案： 【解】
(1)
∵ $PD// AC$, $PE// AB$，
∴ $\angle DPB=\angle C$, $\angle EPC=\angle B$.
∵ $AB=AC$，
∴ $\angle B=\angle C$，
∴ $\angle B=\angle DPB=\angle C=\angle EPC$，
∴ $DB=DP$, $PE=EC$，
∴ 四边形 ADPE 的周长是 $AD+DP+PE+AE=AB+AC=6× 2=12$.
(2)当点 P 运动到 BC 中点时，四边形 ADPE 是菱形. 理由如下：
∵ $PD// AC$, $PE// AB$，
∴ 四边形 ADPE 是平行四边形.
∵ 点 P 是 BC 的中点，
∴ $PB=PC$. 在 $\triangle DBP$ 和 $\triangle ECP$ 中，$\angle B=\angle C$, $BP=CP$，由（1）知 $\angle DPB=\angle EPC$，
∴ $\triangle DBP\cong \triangle ECP$（ASA），
∴ $DP=PE$，
∴ 平行四边形 ADPE 是菱形.
(3)如图，点 P 运动到 $\angle A$ 的平分线上时，四边形 ADPE 是菱形. 理由如下：连接 AP.
∵ $PD// AC$, $PE// AB$，
∴ 四边形 ADPE 是平行四边形.
∵ AP 平分 $\angle BAC$，
∴ $\angle 1=\angle 2$.
∵ $AB// EP$，
∴ $\angle 1=\angle 3$，
∴ $\angle 2=\angle 3$，
∴ $AE=EP$，
∴ 平行四边形 ADPE 是菱形.