《2025年初中必刷题九年级数学上册北师大版》

1[2025甘肃白银校级质检,中]如图,四边形ABCD为平行四边形,延长AD到E,使$DE= AD$,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )

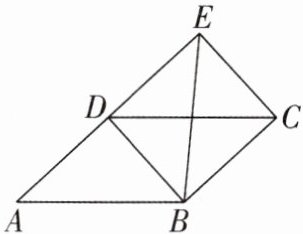
A.$AB= BE$
B.$BE⊥DC$
C.$∠ADB= 90^{\circ }$
D.$CE⊥DE$

答案： B 思路引导：证明一个四边形是矩形的思路：四边形→有三个角是直角→矩形；→平行四边形→对角线相等→矩形；→有一个角是直角→矩形。
【解析】
∵ 四边形ABCD为平行四边形，
∴ AD//BC,AD=BC。
∵ AD=DE，
∴ DE=BC，
∴ 四边形BCED为平行四边形。
∵ AB=BE，DE=AD，
∴ BD⊥AE，
∴ $□ DBCE$为矩形，故A选项不符合题意。对角线互相垂直的平行四边形为菱形，不一定为矩形，故B选项符合题意。
∵ ∠ADB=90°，
∴ ∠EDB=90°，
∴ $□ DBCE$为矩形，故C选项不符合题意。
∵ CE⊥DE，
∴ ∠CED=90°，
∴ $□ DBCE$为矩形，故D选项不符合题意。故选B。

2[2025山西吕梁期末,中]$□ ABCD$中,EF经过两条对角线的交点O,分别交AB,CD于点E,F,在对角线AC上通过作图得到点M,N,如图(1),图(2),图(3),下面关于以点F,M,E,N为顶点的四边形的形状的说法正确的是( )


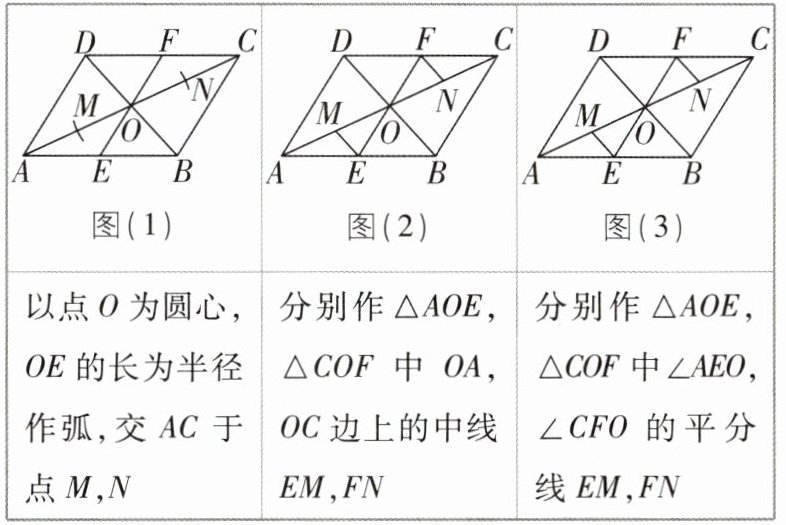
A.都为矩形
B.都为菱形
C.图(1)为平行四边形,图(2)、图(3)为矩形
D.图(1)为矩形,图(2)、图(3)为平行四边形

答案： D 【解析】在平行四边形ABCD中，AB//DC，OA=OC，
∴ ∠FCO=∠EAO,∠CFO=∠AEO。在△FCO和△EAO中，$\left\{\begin{array}{l} ∠FCO=∠EAO,\\ ∠CFO=∠AEO,\\ OC=OA,\end{array}\right.$
∴ $\triangle FCO\cong \triangle EAO(AAS)$，
∴ OE=OF。由题图
(1)作图可得OE=OF=OM=ON，
∴ 题图
(1)中以点F,M,E,N为顶点的四边形为矩形。由题图
(2)作图可得OM=AM=$\frac{1}{2}$OA,ON=NC=$\frac{1}{2}$OC。
∵ OA=OC，
∴ OM=ON。又
∵ OE=OF，
∴ 题图
(2)中以点F,M,E,N为顶点的四边形为平行四边形。由题图
(3)作图可得∠AEM=∠OEM=$\frac{1}{2}$∠AEF,∠CFN=∠NFO=$\frac{1}{2}$∠CFE。
∵ ∠CFE=∠AEF，
∴ ∠OEM=∠NFO。在△EOM和△FON中，$\left\{\begin{array}{l} ∠MOE=∠NOF,\\ OE=OF,\\ ∠OEM=∠OFN,\end{array}\right.$
∴ $\triangle EOM\cong \triangle FON(ASA)$，
∴ OM=ON。又
∵ OE=OF，
∴ 题图
(3)中以点F,M,E,N为顶点的四边形为平行四边形。故选D。

3[2025山东泰安调研,中]如图,在$\triangle ABC$中,直线MN以每秒1个单位的速度从$\triangle ABC$的边BC所在直线的位置出发,沿CA方向平移,交$∠ACB$的平分线于点E,交$\triangle ACB外角∠ACD$的平分线于点F.若$AC= 6$,则当直线MN运动了____秒时,四边形AECF是矩形.

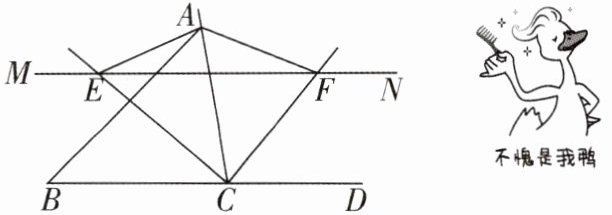
答案： 3 【解析】
∵ MN交∠ACB的平分线于点E，交△ACB外角∠ACD的平分线于点F，
∴ ∠ACE=∠BCE,∠ACF=∠DCF，
∴ ∠ACE+∠ACF=$\frac{1}{2}$×180°=90°，
∴ ∠ECF=90°。设MN与AC交于点O。
∵ MN//BC，
∴ ∠OEC=∠BCE,∠CFO=∠DCF，
∴ ∠OEC=∠ECO,∠CFO=∠OCF，
∴ EO=CO,FO=CO，
∴ OE=OF。当AO=CO=3时，
∵ EO=FO，
∴ 四边形AECF是平行四边形。
∵ ∠ECF=90°，
∴ 平行四边形AECF是矩形，
∴ 当运动了3秒时，四边形AECF是矩形。故答案为3。

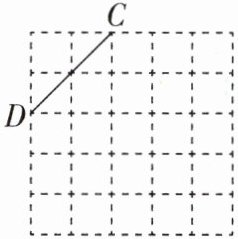
4[2025黑龙江哈尔滨质检,中]如图,$5×5$的正方形网格中,每个小正方形的边长均为1.线段CD的端点在小正方形的顶点上,在图中画一个以线段CD为一边的矩形CDMN,使矩形CDMN的面积是12,并直接写出DN的长.(要求:所画图形的顶点M,N都在小正方形的顶点上)

答案：
【解】如图，矩形CDMN即为所求，连接DN。DN的长为$\sqrt{26}$。由网格的特点可知，∠CDM=∠DMN=∠MNC=90°，
∴ 四边形CDMN为矩形。由勾股定理，得CD=$2\sqrt{2}$，DM=$3\sqrt{2}$，
∴ 矩形CDMN的面积为$2\sqrt{2}×3\sqrt{2}=12$，满足题意。由勾股定理，得DN=$\sqrt{(2\sqrt{2})^{2}+(3\sqrt{2})^{2}}=\sqrt{26}$。

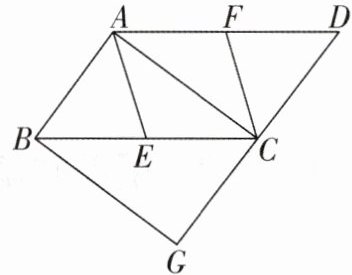
5[2025上海虹口区期末,中]如图,在$□ ABCD$中,E,F分别是边BC,AD的中点,连接AE,CF,AC平分$∠DAE.$
(1)求证:四边形AECF是菱形;
(2)在BC下方作$∠CBG= ∠CAE$,BG与DC的延长线交于点G.求证:四边形ABGC是矩形.

答案： 【证明】
(1)
∵ 四边形ABCD是平行四边形，
∴ AD=BC,AD//BC。
∵ E,F分别是边BC,AD的中点，
∴ AF=CE，
∴ 四边形AECF是平行四边形。
∵ AC平分∠DAE，
∴ ∠EAC=∠FAC。
∵ AF//CE，
∴ ∠FAC=∠ECA，
∴ ∠EAC=∠ACE，
∴ AE=CE，
∴ 平行四边形AECF是菱形。
(2)
∵ E是BC的中点，
∴ BE=CE=AE，
∴ ∠BAE=∠ABE。
∵ ∠ACE+∠ABE+∠BAC=180°，
∴ ∠ACE+∠ABE+∠BAE+∠CAE=180°，
∴ 2(∠BAE+∠CAE)=180°，
∴ ∠BAE+∠CAE=90°，
∴ ∠BAC=90°。
∵ 四边形ABCD是平行四边形，
∴ AB//DC。
∵ ∠CBG=∠CAE，∠CAE=∠ACE，
∴ ∠CBG=∠ACE，
∴ BG//AC，
∴ 四边形ABGC是平行四边形。
∵ ∠BAC=90°，
∴ 平行四边形ABGC是矩形。

6[2024广东深圳福田区调研,较难]如图,在$□ ABCD$中,E,G分别是AB,CD的中点,且$AH= CF,AH// CF.$
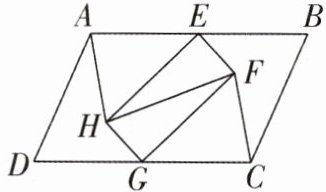
(1)求证:$\triangle AEH\cong \triangle CGF;$
(2)连接FH,HG,EF,若$FH= AD$,求证:四边形EFGH是矩形.

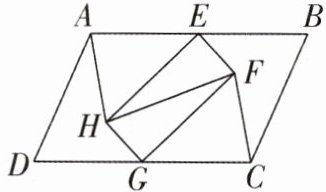
答案： 【证明】
(1)延长AH交CD于点P，延长CF交AB于Q，如图所示。
∵ 四边形ABCD是平行四边形，
∴ AB//CD,AB=CD，
∴ AQ//CP。
∵ AH//CF，
∴ 四边形APCQ是平行四边形，
∴ ∠HAE=∠FCG。
∵ E,G分别是AB,CD的中点，
∴ AE=$\frac{1}{2}$AB,CG=$\frac{1}{2}$CD，
∴ AE=CG=DG。在△AHE和△CFG中，$\left\{\begin{array}{l} AE=CG,\\ ∠HAE=∠FCG,\\ AH=CF,\end{array}\right.$
∴ $\triangle AHE\cong \triangle CFG(SAS)$。
(2)如图，连接EG。
∵ AH//CF，
∴ ∠AHF=∠HFC。由
(1)得$\triangle AHE\cong \triangle CFG$，
∴ ∠AHE=∠CFG,HE=FG，
∴ ∠AHF - ∠AHE=∠HFC - ∠CFG，即∠EHF=∠GFH，
∴ HE//FG，
∴ 四边形EFGH是平行四边形。由
(1)得AE=DG,AB//CD，
∴ 四边形ADGE是平行四边形，
∴ AD=EG。又
∵ FH=AD，
∴ EG=FH，
∴ 四边形EFGH是矩形。