《2025年初中必刷题九年级数学上册北师大版》

1 [2025 河北邯郸调研,中]对于两个不相等的实数 $a,b$,我们规定符号 $\max\{a,b\}$ 表示 $a,b$ 中的较大值,如: $\max\{1,3\}= 3,\max\{-1,-3\}= -1$. 按照这个规定,若 $\max\{x,-x\}= \frac{x^{2}-2x - 1}{2}$,求 $x$ 的值. 甲答: $x= \sqrt{5}+2$ 或 $x= -1$;乙答: $x= 2-\sqrt{5}$;丙答: $x= 1$,则正确的是 ( )

A.只有甲的答案对
B.甲、乙答案合在一起才完整

C.甲、丙答案合在一起才完整
D.三人答案合在一起才完整

答案： A 【解析】当x＞0时,max{x,-x}=x=(x²-2x-1)/2,整理,得x²-4x=1,配方,得x²-4x+4=1+4,即(x-2)²=5,直接开平方,得x-2=±√5,解得x₁=2+√5,x₂=2-√5(不合题意,舍去);当x＜0时,max{x,-x}=-x=(x²-2x-1)/2,整理,得x²=1,解得x₁=-1,x₂=1(不合题意,舍去).综上,x=√5+2或x=-1,故只有甲的答案对. 故选A.

2 [2024 浙江绍兴期末,中]已知 $9x^{2}+18(n - 1)x + 18n$ 是完全平方式,则常数 $n$ 的值是______.

答案： 2±√3 【解析】
∵原式=(3x)²±2×3x×3√2n+(3√2n)²=(3x±3√2n)²,
∴±18√2n=18(n-1),即(n-1)²=2n,
∴n²-4n+1=0,则n²-4n+4-4+1=0,即(n-2)²=3,
∴n-2=±√3,
∴n=2±√3. 故答案为2±√3.

3 判断代数式的正负 [2025 山东枣庄期末,中]无论 $a,b$ 为何值,代数式 $a^{2}+4b^{2}+8a - 12b + 26$ 的值总是 ( )

A.非负数
B.正数
C.0
D.负数

答案： B 【解析】a²+4b²+8a-12b+26=(a+4)²-16+(2b-3)²-9+26=(a+4)²+(2b-3)²+1.
∵(a+4)²≥0,(2b-3)²≥0,
∴a²+4b²+8a-12b+26≥1. 故选B.

4 比较大小 [2025 江苏徐州期中,中]若 $m$ 为实数, $P= -m^{2}-m + 1,Q= m^{2}-5m + 4$,则比较 $P,Q$ 的大小可得______.

答案： P＜Q 【解析】Q-P=(m²-5m+4)-(-m²-m+1)=m²-5m+4+m²+m-1=2m²-4m+3=2(m-1)²+1.
∵(m-1)²≥0,
∴2(m-1)²+1＞0,
∴Q-P＞0,
∴P＜Q,故答案为P＜Q.

5 判断三角形形状 [2025 广东揭阳期中,中]若 $a,b,c$ 为 $\triangle ABC$ 的三边长,且满足 $a^{2}+b^{2}+c^{2}-ab - bc - ca = 0$,则 $\triangle ABC$ 的形状是______三角形.

答案： 等边 【解析】
∵a²+b²+c²-ab-bc-ca=0,
∴2a²+2b²+2c²-2ab-2bc-2ca=0,
∴(a²-2ab+b²)+(b²-2bc+c²)+(c²-2ca+a²)=0,
∴(a-b)²+(b-c)²+(c-a)²=0,
∴a-b=0,b-c=0,c-a=0,
∴a=b=c,
∴△ABC是等边三角形.

6 求最值 [2025 山西吕梁质检,较难]阅读与思考:配方法不仅能够帮助我们解一元二次方程,还能用来解决最值问题,例如:求代数式 $2x^{2}-x + 2 + y^{2}$ 的最小值,解法如下:
解:原式 $=2(x^{2}-\frac{1}{2}x)+2 + y^{2}= 2(x^{2}-\frac{1}{2}x+\frac{1}{16}-\frac{1}{16})+2 + y^{2}= 2(x^{2}-\frac{1}{2}x+\frac{1}{16})-\frac{1}{8}+2 + y^{2}= 2(x-\frac{1}{4})^{2}+y^{2}+\frac{15}{8}$. $\because 2(x-\frac{1}{4})^{2}\geq0,y^{2}\geq0$, $\therefore 2(x-\frac{1}{4})^{2}+y^{2}+\frac{15}{8}\geq\frac{15}{8}$, $\therefore 2x^{2}-x + 2 + y^{2}$ 的最小值是 $\frac{15}{8}$.
根据材料中的方法,解答下列问题.
(1) $-x^{2}+4x - 1$ 的最大值为______;
(2)求 $m^{2}+n^{2}+6m - 4n + 15$ 的最小值.

答案： 【解】
(1)-x²+4x-1=-(x²-4x)-1=-(x²-4x+4-4)-1=-(x-2)²+4-1=-(x-2)²+3.
∵-(x-2)²≤0,
∴-(x-2)²+3≤3,
∴-(x-2)²+3的最大值为3,
∴-x²+4x-1的最大值为3. 故答案为3.
(2)m²+n²+6m-4n+15=(m²+6m+9)+(n²-4n+4)+2=(m+3)²+(n-2)²+2.
∵(m+3)²≥0,(n-2)²≥0,
∴(m+3)²+(n-2)²+2≥2,
∴(m+3)²+(n-2)²+2的最小值为2,
∴m²+n²+6m-4n+15的最小值为2.

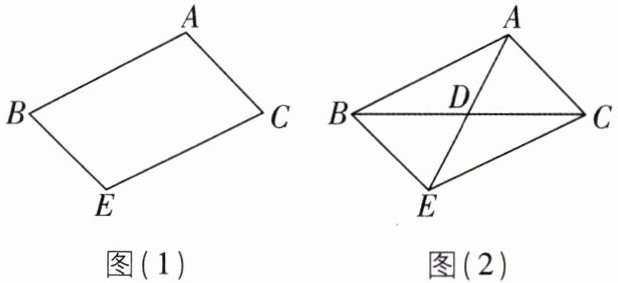
7 核心素养 几何直观 [2025 黑龙江哈尔滨校级期中,中]如图(1),四边形 $ABEC$ 中, $AB$ 平行于 $CE$, $\angle B= \angle C$.
(1)求证: $AB = CE$;
(2)如图(2),连接 $AE,BC$ 交于点 $D$,若四边形 $ABEC$ 的面积为 60,求 $\triangle ADC$ 的面积;
(3)在(2)的条件下, $\angle BAC+\angle DAC = 180^{\circ},AD = 5$,求 $AC$ 的长.
]

答案：
(1)【证明】
∵AB//CE,
∴∠B +∠E=180°.
∵∠B=∠C,
∴∠C +∠E=180°,
∴BE//AC,
∴四边形ABEC是平行四边形,
∴AB=CE.【解】
(2)由
(1)可知,四边形ABEC是平行四边形,
∴S△ABC=S△BEC,D是BC的中点.
∵四边形ABEC的面积为60,
∴S△ABC=1/2S四边形ABEC=30.
∵D是BC的中点,
∴S△ADC=S△ADB=1/2＜/think＞＜/think＞S△ABC=15.
(3)
∵四边形ABEC是平行四边形,
∴AE=2AD=10.
∵AB//CE,
∴∠BAC+∠ACE=180°.
∵∠BAC+∠DAC=180°,
∴∠ACE=∠DAC,
∴AE=CE=10. 如图,过点E作EF⊥AC,交AC于点F,
∴AF=CF=1/2AC. 设CF=x,则AC=2x. 在Rt△CFE中,EF=√(CE²-CF²)=√(100-x²).
∵S四边形ABEC=AC·EF=60,
∴2x·√(100-x²)=60,
∴4x²(100-x²)=3600,令x²=a,则4a(100-a)=3600,即4a²-400a=-3600,配方,得4a²-400a+10000=-3600+10000,即(2a-100)²=6400,开方,得2a-100=±80,解得a=10或a=90. 当a=10时,x²=10,解得x=√10或x=-√10(舍去),
∴AC=2x=2√10. 当a=90时,x²=90,解得x=3√10或x=-3√10(舍去),
∴AC=2x=6√10. 综上可知,AC的长为2√10或6√10.