第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025陕西西安校级质检,中]在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数分布表:
|试验种子个数n|5|50|100|200|500|1000|2000|3000|
|发芽种子个数m|4|45|92|188|476|951|1900|2850|
|发芽频率$\frac{m}{n}$|0.80|0.90|0.92|0.94|0.952|0.951|0.95|0.95|
根据试验结果,若要使发芽种子个数至少为2500,则以下四个数与至少需要的试验种子个数最接近的为( )
A.2500
B.2700
C.2800
D.3000
|试验种子个数n|5|50|100|200|500|1000|2000|3000|
|发芽种子个数m|4|45|92|188|476|951|1900|2850|
|发芽频率$\frac{m}{n}$|0.80|0.90|0.92|0.94|0.952|0.951|0.95|0.95|
根据试验结果,若要使发芽种子个数至少为2500,则以下四个数与至少需要的试验种子个数最接近的为( )
A.2500
B.2700
C.2800
D.3000
答案:
B 【解析】观察题表可得种子发芽的概率估计值为0.95.设需要的试验种子个数为 x.根据题意,得95%x = 2500,解得 x≈2632.
∴ 要使发芽种子个数至少为2500,与至少需要的试验种子个数最接近的数为2700,故选 B.
∴ 要使发芽种子个数至少为2500,与至少需要的试验种子个数最接近的数为2700,故选 B.
2 [新考法][2024湖北武汉调研,中]根据频率估计概率原理,可以用随机模拟的方法对圆周率$\pi$进行估计.用计算机随机产生m个有序数对$(x,y)(0\leqslant x\leqslant 1,0\leqslant y\leqslant 1)$,它们对应的点全部在平面直角坐标系中某一个正方形的边界及其内部.若统计出这些点中到原点的距离小于或等于1的点有n个,则可估计$\pi$的值是______.
答案:
$\frac{4n}{m}$
【解析】根据题意可知,有 n 个有序数对(x,y)对应的点落在 中的阴影部分,
中的阴影部分,
∴ 每个点落在阴影部分的频率为$\frac{n}{m}$,每个点落在阴影部分的概率为$\frac{\frac{1}{4}\pi}{1}$.
∵ 当试验次数足够多时,可用频率估计概率,
∴ $\frac{\frac{1}{4}\pi}{1}\approx\frac{n}{m}$,解得π≈$\frac{4n}{m}$.
∴ 可估计π的值为$\frac{4n}{m}$.
思路分析:根据落在阴影部分的点的个数与正方形内的点的个数之比等于两者面积之比得出$\frac{\frac{1}{4}\pi}{1}\approx\frac{n}{m}$,进而可得答案.
$\frac{4n}{m}$
【解析】根据题意可知,有 n 个有序数对(x,y)对应的点落在
 中的阴影部分,
中的阴影部分,∴ 每个点落在阴影部分的频率为$\frac{n}{m}$,每个点落在阴影部分的概率为$\frac{\frac{1}{4}\pi}{1}$.
∵ 当试验次数足够多时,可用频率估计概率,
∴ $\frac{\frac{1}{4}\pi}{1}\approx\frac{n}{m}$,解得π≈$\frac{4n}{m}$.
∴ 可估计π的值为$\frac{4n}{m}$.
思路分析:根据落在阴影部分的点的个数与正方形内的点的个数之比等于两者面积之比得出$\frac{\frac{1}{4}\pi}{1}\approx\frac{n}{m}$,进而可得答案.
3 [中]如图(1)所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个长为5m,宽为4m的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在边界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了图(2)所示的折线统计图,由此他估计不规则图案的面积大约为$______m^2($结果取整数).

答案:
7 【解析】假设不规则图案面积为$x\ \text{m}^2$,由已知得长方形面积为20$\text{m}^2$,则小球落在不规则图案的概率为$\frac{x}{20}$.当事件 A 试验次数足够多,即样本足够大时,其频率可作为事件 A 发生概率的估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,所以$\frac{x}{20}=0.35$,解得 x = 7.故答案为7.
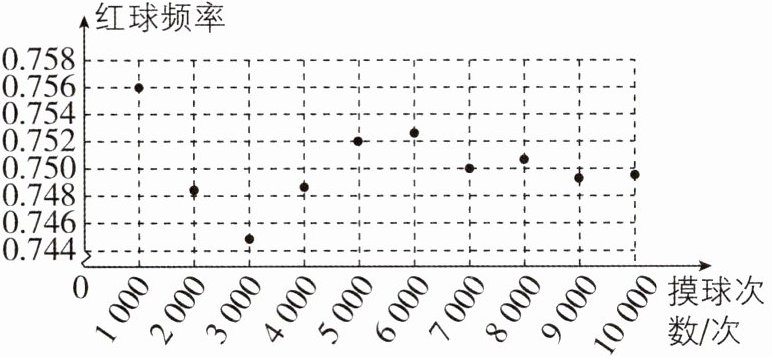
4 [2025北京海淀区校级质检,较难]在学习“用频率估计概率”这一节时,小明和他的伙伴们设计了一个摸球试验:在一个不透明帆布袋中装有白球和红球共4个,这4个球除颜色外无其他差别,每次摸球前先将袋中的球搅匀,然后从袋中随机摸出1个球,观察该球的颜色并记录,再把它放回,在老师的帮助下,小明和他的伙伴们用计算机模拟这个摸球试验,如图是这个试验中摸出一个球是红球的结果.
(1)根据所学的频率与概率关系的知识,估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是______,其中红球的个数是______;
(2)如果从这个不透明的帆布袋中同时摸出两个球,用列表法求摸出的两个球刚好是一个红球和一个白球的概率;
(3)在这个不透明的帆布袋中再放入n个白球,那么(2)中所求的概率将变为______(用n表示).

(1)根据所学的频率与概率关系的知识,估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是______,其中红球的个数是______;
(2)如果从这个不透明的帆布袋中同时摸出两个球,用列表法求摸出的两个球刚好是一个红球和一个白球的概率;
(3)在这个不透明的帆布袋中再放入n个白球,那么(2)中所求的概率将变为______(用n表示).
答案:
【解】
(1)由题图可知,随着摸球次数的增加,摸出红球的频率逐渐稳定在0.75附近,则可估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是0.75,其中红球的个数是4×0.75 = 3.故答案为0.75,3.
(2)将3个红球分别记为红1,红2,红3,列表如下:
从表中可以看出,从不透明的帆布袋中同时摸出两个球,可能出现的结果共有12种,且这些结果出现的可能性相等,其中摸出的两个球刚好是一个红球和一个白球的结果共有6种,概率为$\frac{6}{12}=\frac{1}{2}$.
(3)在这个不透明的帆布袋中再放入 n 个白球后,同时摸出两个球,易知可能出现的结果共有$(n + 4)(n + 3)=(n^2 + 7n + 12)$种,且这些结果出现的可能性相等,其中摸出的两个球刚好是一个红球和一个白球的结果共有$(n + 1)×3×2=(6n + 6)$种,所求概率为$\frac{6n + 6}{n^2 + 7n + 12}$.故答案为$\frac{6n + 6}{n^2 + 7n + 12}$.
学有所得:频率是个试验统计值,具有随机性,可能取多个数值,因此只能近似地反映事件发生可能性的大小;概率是个理论值,是由事件的本质所决定的,只能取唯一值,它能精确地反映事件发生可能性的大小.
(1)由题图可知,随着摸球次数的增加,摸出红球的频率逐渐稳定在0.75附近,则可估计从这个不透明的帆布袋中随机摸出一个球是红球的概率是0.75,其中红球的个数是4×0.75 = 3.故答案为0.75,3.
(2)将3个红球分别记为红1,红2,红3,列表如下:
从表中可以看出,从不透明的帆布袋中同时摸出两个球,可能出现的结果共有12种,且这些结果出现的可能性相等,其中摸出的两个球刚好是一个红球和一个白球的结果共有6种,概率为$\frac{6}{12}=\frac{1}{2}$.
(3)在这个不透明的帆布袋中再放入 n 个白球后,同时摸出两个球,易知可能出现的结果共有$(n + 4)(n + 3)=(n^2 + 7n + 12)$种,且这些结果出现的可能性相等,其中摸出的两个球刚好是一个红球和一个白球的结果共有$(n + 1)×3×2=(6n + 6)$种,所求概率为$\frac{6n + 6}{n^2 + 7n + 12}$.故答案为$\frac{6n + 6}{n^2 + 7n + 12}$.
学有所得:频率是个试验统计值,具有随机性,可能取多个数值,因此只能近似地反映事件发生可能性的大小;概率是个理论值,是由事件的本质所决定的,只能取唯一值,它能精确地反映事件发生可能性的大小.
查看更多完整答案,请扫码查看


