第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2025浙江杭州校级质检]已知P为线段AB的黄金分割点,且AP<PB,则( )
A.$AP^{2}= AB\cdot PB$
B.$AB^{2}= AP\cdot PB$
C.$PB^{2}= AP\cdot AB$
D.$AP\cdot BP= AB$
A.$AP^{2}= AB\cdot PB$
B.$AB^{2}= AP\cdot PB$
C.$PB^{2}= AP\cdot AB$
D.$AP\cdot BP= AB$
答案:
C 【解析】
∵ P 为线段 AB 的黄金分割点,且AP<PB,
∴ $\frac{PB}{AB}=\frac{AP}{PB}$,即 $PB^{2}=AP\cdot AB$。故选 C。
∵ P 为线段 AB 的黄金分割点,且AP<PB,
∴ $\frac{PB}{AB}=\frac{AP}{PB}$,即 $PB^{2}=AP\cdot AB$。故选 C。
2[2024江西九江质检]点B把线段AC分成两部分,如果$\frac {BC}{AB}= \frac {AB}{AC}= k$,那么k的值为____.
答案:
$\frac{\sqrt{5}-1}{2}$ 【解析】
∵ 点 B 把线段 AC 分成两部分,$\frac{BC}{AB}=\frac{AB}{AC}=k$,
∴ 点 B 是线段 AC 的黄金分割点,AB>BC,
∴ $k=\frac{\sqrt{5}-1}{2}$,故答案为 $\frac{\sqrt{5}-1}{2}$。
∵ 点 B 把线段 AC 分成两部分,$\frac{BC}{AB}=\frac{AB}{AC}=k$,
∴ 点 B 是线段 AC 的黄金分割点,AB>BC,
∴ $k=\frac{\sqrt{5}-1}{2}$,故答案为 $\frac{\sqrt{5}-1}{2}$。
3已知点C是线段AB的黄金分割点,且BC= AC+2,则AB的长为____.
答案:
$2\sqrt{5}+4$ 【解析】
∵ $BC=AC+2$,
∴ BC>AC,
∴ $BC=\frac{\sqrt{5}-1}{2}AB$,$AC=AB-BC=\frac{3-\sqrt{5}}{2}AB$,
∴ $\frac{\sqrt{5}-1}{2}AB=\frac{3-\sqrt{5}}{2}AB+2$,
∴ $(\sqrt{5}-2)AB=2$,
∴ $AB=\frac{2}{\sqrt{5}-2}=\frac{2(\sqrt{5}+2)}{(\sqrt{5}-2)(\sqrt{5}+2)}=2\sqrt{5}+4$。故答案为 $2\sqrt{5}+4$。
∵ $BC=AC+2$,
∴ BC>AC,
∴ $BC=\frac{\sqrt{5}-1}{2}AB$,$AC=AB-BC=\frac{3-\sqrt{5}}{2}AB$,
∴ $\frac{\sqrt{5}-1}{2}AB=\frac{3-\sqrt{5}}{2}AB+2$,
∴ $(\sqrt{5}-2)AB=2$,
∴ $AB=\frac{2}{\sqrt{5}-2}=\frac{2(\sqrt{5}+2)}{(\sqrt{5}-2)(\sqrt{5}+2)}=2\sqrt{5}+4$。故答案为 $2\sqrt{5}+4$。
4定义:如图(1),点P在线段MN上,若满足$MP^{2}= PN\cdot MN$,则称点P为线段MN的黄金分割点.如图(2),在$\triangle ABC$中,$AB= AC= 1,∠A= 36^{\circ }$,BD平分$∠ABC$,交AC于点D.
(1)求证:点D是线段AC的黄金分割点.
(2)求出线段AD的长.
]

(1)求证:点D是线段AC的黄金分割点.
(2)求出线段AD的长.
]

答案:
(1)【证明】
∵ $\angle A=36^{\circ}$,$AB=AC$,
∴ $\angle ABC=\angle C=72^{\circ}$。又
∵ BD 平分 $\angle ABC$,
∴ $\angle DBC=\angle ABD=36^{\circ}=\angle A$,
∴ $AD=BD$。
∵ $\angle BDC=\angle A+\angle ABD=72^{\circ}=\angle C$,
∴ $BD=BC$,
∴ $AD=BD=BC$。在$\triangle ABC$与$\triangle BDC$中,
∵ $\angle A=\angle DBC$,$\angle C=\angle C$,
∴ $\triangle ABC\backsim\triangle BDC$,
∴ $\frac{AC}{BC}=\frac{BC}{DC}$,即 $BC^{2}=AC\cdot DC$,即 $AD^{2}=AC\cdot DC$,
∴ 点 D 是线段 AC 的黄金分割点。
(2)【解】设 $AD=x$,则 $DC=1-x$。由
(1)中的结论,得 $x^{2}=1-x$。解得 $x=\frac{\sqrt{5}}{2}-\frac{1}{2}$或 $x=-\frac{\sqrt{5}}{2}-\frac{1}{2}$(舍去),
∴ $AD=\frac{\sqrt{5}-1}{2}$。
(1)【证明】
∵ $\angle A=36^{\circ}$,$AB=AC$,
∴ $\angle ABC=\angle C=72^{\circ}$。又
∵ BD 平分 $\angle ABC$,
∴ $\angle DBC=\angle ABD=36^{\circ}=\angle A$,
∴ $AD=BD$。
∵ $\angle BDC=\angle A+\angle ABD=72^{\circ}=\angle C$,
∴ $BD=BC$,
∴ $AD=BD=BC$。在$\triangle ABC$与$\triangle BDC$中,
∵ $\angle A=\angle DBC$,$\angle C=\angle C$,
∴ $\triangle ABC\backsim\triangle BDC$,
∴ $\frac{AC}{BC}=\frac{BC}{DC}$,即 $BC^{2}=AC\cdot DC$,即 $AD^{2}=AC\cdot DC$,
∴ 点 D 是线段 AC 的黄金分割点。
(2)【解】设 $AD=x$,则 $DC=1-x$。由
(1)中的结论,得 $x^{2}=1-x$。解得 $x=\frac{\sqrt{5}}{2}-\frac{1}{2}$或 $x=-\frac{\sqrt{5}}{2}-\frac{1}{2}$(舍去),
∴ $AD=\frac{\sqrt{5}-1}{2}$。
5鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比例,是自然界最美的鬼斧神工.如图,点P是AB的黄金分割点(AP>BP),若线段AB的长为6cm,则AP的长为( )
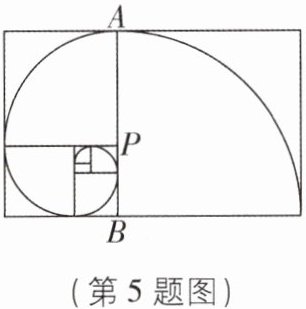
A.$(3\sqrt {5}-3)cm$
B.$(3-\sqrt {5})cm$
C.$(9-3\sqrt {5})cm$
D.$(\sqrt {5}-1)cm$
]

A.$(3\sqrt {5}-3)cm$
B.$(3-\sqrt {5})cm$
C.$(9-3\sqrt {5})cm$
D.$(\sqrt {5}-1)cm$
]
答案:
A 【解析】
∵ 点 P 是 AB 的黄金分割点($AP>BP$),$AB=6\space cm$,
∴ $AP=\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×6=(3\sqrt{5}-3)\space cm$,故选 A。
∵ 点 P 是 AB 的黄金分割点($AP>BP$),$AB=6\space cm$,
∴ $AP=\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×6=(3\sqrt{5}-3)\space cm$,故选 A。
6[2025广西河池质检]宽与长的比是$\frac {\sqrt {5}-1}{2}$的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调、匀称的美感.如图,现按照如下的步骤作图:
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于F.
则所作图形中是黄金矩形的是( )
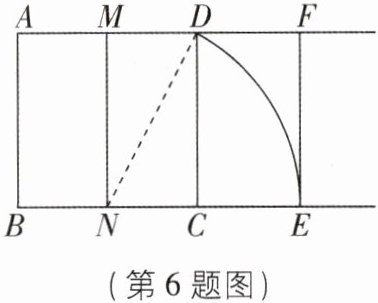
A.矩形MNCD
B.矩形DCEF
C.矩形MNEF
D.矩形DCEF和矩形ABEF
]
第一步:作一个正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以点N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD,交AD的延长线于F.
则所作图形中是黄金矩形的是( )

A.矩形MNCD
B.矩形DCEF
C.矩形MNEF
D.矩形DCEF和矩形ABEF
]
答案:
D 【解析】设正方形 ABCD 的边长为 $2a$。A 选项,
∵ 点 N 是 BC 的中点,
∴ $BN=CN=\frac{1}{2}BC=a$,
∴ $\frac{CN}{CD}=\frac{a}{2a}=\frac{1}{2}\neq\frac{\sqrt{5}-1}{2}$,
∴ 矩形 MNCD 不是黄金矩形。B 选项,在 $Rt\triangle DCN$中,$CN=a$,$CD=2a$,
∴ $DN=\sqrt{CN^{2}+CD^{2}}=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$。由题意得 $DN=NE=\sqrt{5}a$,
∴ $CE=EN-CN=(\sqrt{5}-1)a$,
∴ $\frac{CE}{CD}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$,
∴ 矩形 DCEF 是黄金矩形。C 选项,
∵ 四边形 DCEF 是矩形,
∴ $EF=CD=2a$,
∴ $\frac{EF}{NE}=\frac{2a}{\sqrt{5}a}=\frac{2\sqrt{5}}{5}\neq\frac{\sqrt{5}-1}{2}$,
∴ 矩形 MNEF 不是黄金矩形。D 选项,
∵ $BN=a$,$NE=\sqrt{5}a$,
∴ $BE=BN+NE=(\sqrt{5}+1)a$,
∴ $\frac{AB}{BE}=\frac{2a}{(\sqrt{5}+1)a}=\frac{2}{\sqrt{5}+1}=\frac{\sqrt{5}-1}{2}$,
∴ 矩形 ABEF 是黄金矩形,
∴ 矩形 DCEF 和矩形 ABEF 都是黄金矩形。故选 D。
∵ 点 N 是 BC 的中点,
∴ $BN=CN=\frac{1}{2}BC=a$,
∴ $\frac{CN}{CD}=\frac{a}{2a}=\frac{1}{2}\neq\frac{\sqrt{5}-1}{2}$,
∴ 矩形 MNCD 不是黄金矩形。B 选项,在 $Rt\triangle DCN$中,$CN=a$,$CD=2a$,
∴ $DN=\sqrt{CN^{2}+CD^{2}}=\sqrt{a^{2}+(2a)^{2}}=\sqrt{5}a$。由题意得 $DN=NE=\sqrt{5}a$,
∴ $CE=EN-CN=(\sqrt{5}-1)a$,
∴ $\frac{CE}{CD}=\frac{(\sqrt{5}-1)a}{2a}=\frac{\sqrt{5}-1}{2}$,
∴ 矩形 DCEF 是黄金矩形。C 选项,
∵ 四边形 DCEF 是矩形,
∴ $EF=CD=2a$,
∴ $\frac{EF}{NE}=\frac{2a}{\sqrt{5}a}=\frac{2\sqrt{5}}{5}\neq\frac{\sqrt{5}-1}{2}$,
∴ 矩形 MNEF 不是黄金矩形。D 选项,
∵ $BN=a$,$NE=\sqrt{5}a$,
∴ $BE=BN+NE=(\sqrt{5}+1)a$,
∴ $\frac{AB}{BE}=\frac{2a}{(\sqrt{5}+1)a}=\frac{2}{\sqrt{5}+1}=\frac{\sqrt{5}-1}{2}$,
∴ 矩形 ABEF 是黄金矩形,
∴ 矩形 DCEF 和矩形 ABEF 都是黄金矩形。故选 D。
7主持人主持节目时,站在舞台的黄金分割点处最自然得体.如图所示,如果舞台AB的长为12米,一名主持人现在站在A处,则她要到达最理想的位置至少走____米.
]

]

答案:
$18-6\sqrt{5}$ 【解析】如图所示,$AP<BP$,所以 $AP=12×(1-\frac{\sqrt{5}-1}{2})=(18-6\sqrt{5})$米,即至少走$(18-6\sqrt{5})$米。
8当一个人的上半身(肚脐以上的高度)与下半身(肚脐以下的高度)的比值越接近黄金分割比0.618时,越给人一种美感.某位参加空姐选拔的选手身高为165cm,上半身长65cm,那么她穿____cm的鞋子才更美.(精确到1cm)
答案:
5 【解析】设她穿 $x\space cm$的鞋子才更美。根据题意,得 $\frac{65}{165-65+x}=0.618$,解得 $x\approx5$。经检验,$x\approx5$是原方程的解,且符合题意,所以她穿5 cm 的鞋子才更美。故答案为 5。
9[2024浙江温州鹿城区期末]如图,点E是正方形ABCD的边AB上的黄金分割点,且AE>EB,以AE为边作正方形AEHF,F在AD上,延长EH交CD于点I,连接BF交EI于点G,连接BI,则$S_{\triangle BCI}:S_{\triangle FGH}$的值为____.
]
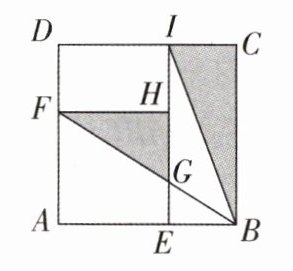
]

答案:
$\frac{\sqrt{5}+1}{2}$ 【解析】
∵ 四边形 ABCD 是正方形,
∴ $BC=CD=DA=AB$。
∵ 点 E 是正方形 ABCD 的边 AB 上的黄金分割点,且 $AE>EB$,
∴ $\frac{AE}{AB}=\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$。
∵ 四边形 AEHF 是正方形,
∴ $EH=HF=FA=AE$,$FH// AE$,
∴ 易证$\triangle FHG\backsim\triangle BEG$,
∴ $\frac{GH}{GE}=\frac{FH}{BE}$,
∴ $\frac{GH}{GH+GE}=\frac{GH}{HE}=\frac{FH}{FH+BE}=\frac{AE}{AE+BE}=\frac{AE}{AB}=\frac{\sqrt{5}-1}{2}$,
∴ $GH=\frac{\sqrt{5}-1}{2}HE=\frac{\sqrt{5}-1}{2}AE$。
∵ $\angle C=\angle CBE=\angle BEI=90^{\circ}$,
∴ 四边形 BCIE 是矩形,
∴ $IC=BE$,
∴ $S_{\triangle BCI}:S_{\triangle FGH}=\frac{\frac{1}{2}BC\cdot IC}{\frac{1}{2}FH\cdot HG}=\frac{AB\cdot BE}{AE\cdot HG}=\frac{BE}{AE}\cdot\frac{AB}{HG}=\frac{\sqrt{5}-1}{2}\cdot\frac{AB}{\frac{\sqrt{5}-1}{2}AE}=\frac{\sqrt{5}-1}{2}\cdot\frac{1}{\frac{\sqrt{5}-1}{2}×\frac{\sqrt{5}-1}{2}}=\frac{2}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{2}$。故答案为 $\frac{\sqrt{5}+1}{2}$。
∵ 四边形 ABCD 是正方形,
∴ $BC=CD=DA=AB$。
∵ 点 E 是正方形 ABCD 的边 AB 上的黄金分割点,且 $AE>EB$,
∴ $\frac{AE}{AB}=\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$。
∵ 四边形 AEHF 是正方形,
∴ $EH=HF=FA=AE$,$FH// AE$,
∴ 易证$\triangle FHG\backsim\triangle BEG$,
∴ $\frac{GH}{GE}=\frac{FH}{BE}$,
∴ $\frac{GH}{GH+GE}=\frac{GH}{HE}=\frac{FH}{FH+BE}=\frac{AE}{AE+BE}=\frac{AE}{AB}=\frac{\sqrt{5}-1}{2}$,
∴ $GH=\frac{\sqrt{5}-1}{2}HE=\frac{\sqrt{5}-1}{2}AE$。
∵ $\angle C=\angle CBE=\angle BEI=90^{\circ}$,
∴ 四边形 BCIE 是矩形,
∴ $IC=BE$,
∴ $S_{\triangle BCI}:S_{\triangle FGH}=\frac{\frac{1}{2}BC\cdot IC}{\frac{1}{2}FH\cdot HG}=\frac{AB\cdot BE}{AE\cdot HG}=\frac{BE}{AE}\cdot\frac{AB}{HG}=\frac{\sqrt{5}-1}{2}\cdot\frac{AB}{\frac{\sqrt{5}-1}{2}AE}=\frac{\sqrt{5}-1}{2}\cdot\frac{1}{\frac{\sqrt{5}-1}{2}×\frac{\sqrt{5}-1}{2}}=\frac{2}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{2}$。故答案为 $\frac{\sqrt{5}+1}{2}$。
10已知点C是线段AB的黄金分割点,且AB= 6cm,则BC的长为____cm.
答案:
$(3\sqrt{5}-3)$或$(9-3\sqrt{5})$ 【解析】
∵ 点 C 是线段 AB 的黄金分割点,且 $AB=6\space cm$,
∴ $BC=\frac{\sqrt{5}-1}{2}AB=(3\sqrt{5}-3)\space cm$或$BC=AB-\frac{\sqrt{5}-1}{2}AB=(9-3\sqrt{5})\space cm$。
∵ 点 C 是线段 AB 的黄金分割点,且 $AB=6\space cm$,
∴ $BC=\frac{\sqrt{5}-1}{2}AB=(3\sqrt{5}-3)\space cm$或$BC=AB-\frac{\sqrt{5}-1}{2}AB=(9-3\sqrt{5})\space cm$。
查看更多完整答案,请扫码查看


