《2025年初中必刷题九年级数学上册北师大版》

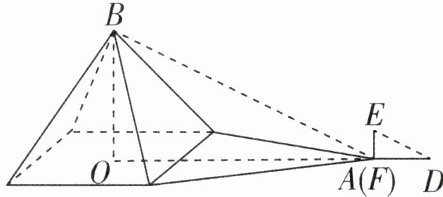
1 [2025 北京东城区质检]古希腊科学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶点处直立一根木杆,借助太阳光测量出了金字塔的高度.如图,木杆 EF 长 2 米,它的影长 FD 是 4 米,同一时刻测得 OA 长 268 米,则金字塔的高度 BO 是______米.
]

答案： 134 【解析】根据题意易得△BOA∽△EFD，
∴$\frac{FD}{OA}=\frac{EF}{BO}$。设金字塔的高度 BO 为 x 米，则$\frac{4}{268}=\frac{2}{x}$，解得$x = 134$，经检验，$x = 134$是原方程的解，
∴ BO = 134 米。

2 如图,花丛中有一路灯杆 AB.在灯光下,小明在 D 点处的影长 DE = 3 米,沿 BD 方向行走到达 G 点,DG = 5 米,这时小明的影长 GH = 5 米.如果小明的身高为 1.7 米,求路灯杆 AB 的高度.
]

答案： 【解】由题意得，CD//AB，所以易证△CDE∽△ABE，所以$\frac{CD}{AB}=\frac{DE}{BE}$，即$\frac{1.7}{AB}=\frac{3}{3 + BD}$。①
同理，△FGH∽△ABH，所以$\frac{FG}{AB}=\frac{GH}{BH}$，即$\frac{1.7}{AB}=\frac{5}{5 + 5 + BD}$。②
思路分析：延长 DF 交 AB 于 C，构造相似三角形，从而利用相似求相应长度。
思路分析：过点 E 作水平线交 AB 于点 G，交 CD 于点 H，结合题意证出△CHE∽△AGE，再根据对应边成比例解答即可。
联立①②，解得 BD = 7.5, AB = 5.95。
答：路灯杆 AB 的高度为 5.95 米。

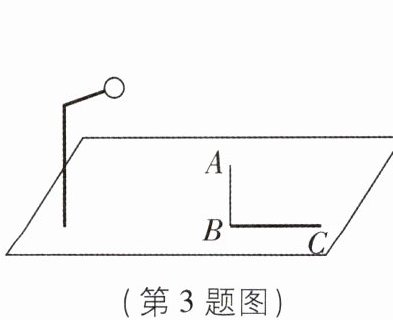
3 [2025 山西太原期末]如图,为了确定路灯灯泡到地面的距离,小明与小亮选取了长 1 米的标杆 AB,小明测得标杆在路灯下的影长 BC = 1.5 米,从点 B 出发沿着 CB 方向行走 7.5 米后恰好走到路灯灯泡的正下方.据此可得,路灯灯泡到地面的距离为( )

A.5.6 米
B.6 米
C.6.4 米
D.7.5 米

答案：
B 【解析】如图，路灯灯泡的位置记为 D，作 DE⊥BC 交 CB 延长线于 E，连接 DC，则 DC 经过点 A，DE 长即为灯泡到地面的距离。由题意，得 AB = 1m，BC = 1.5m，CE = 1.5 + 7.5 = 9(m)。
∵AB//DE，
∴易得△ABC∽△DEC，
∴$\frac{AB}{DE}=\frac{CB}{CE}$，
∴$\frac{1}{DE}=\frac{1.5}{9}$，
∴DE = 6m，
∴路灯灯泡到地面的距离为 6m。故选 B。

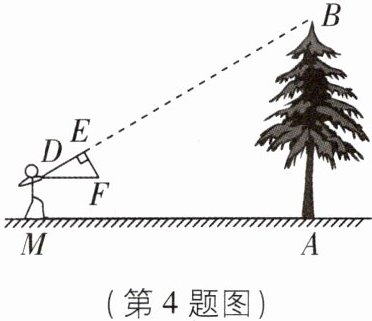
4 [2024 北京延庆区期末]如图,小明用自制的直角三角形标尺 DEF 测量树的高度 AB.他调整自己的位置,设法使斜边 DF 保持水平,并且边 DE 与点 B 在同一直线上,已知标尺的两条直角边 DE = 40 cm,EF = 30 cm,测得边 DF 离地面的高度 DM = 1.5 m,小明与树的距离 AM = 10 m,则树高 AB 是______m.

答案： 9 【解析】延长 DF 交 AB 于 C，则 DC⊥AB，
∴∠DEF = ∠BCD = 90°。又
∵∠EDF = ∠CDB，
∴△DEF∽△DCB，
∴$\frac{EF}{BC}=\frac{DE}{DC}$。
∵DE = 40cm = 0.4m，EF = 30cm = 0.3m，CD = AM = 10m，
∴$\frac{0.3}{BC}=\frac{0.4}{10}$，
∴BC = 7.5m。
∵AC = DM = 1.5m，
∴AB = AC + BC = 1.5 + "7.5" = 9(m)。故答案为 9。

5 [2025 广东佛山质检]如图,九年级(1)班课外活动小组想利用标杆测量佛山千灯湖市民广场醒狮雕塑的高度,已知点 A,C,E 在同一直线上,标杆高度 CD = 2.8 m,标杆与雕塑的水平距离 BD = 20 m,人的眼睛与地面的高度 EF = 1.8 m,人与标杆 CD 的水平距离 DF = 2 m,求醒狮雕塑 AB 的高度.
]

答案：
【解】如图所示，过点 E 作 EH⊥AB 于 H，线段 EH 与线段 CD 交于点 G，则易得∠CGE = ∠AHE = 90°，四边形 EFBH，四边形 BDGH，四边形 EFDG 是矩形，
∴BD = GH = 20m，EG = DF = 2m，EF = DG = BH = 1.8m。
∵∠CEG = ∠AEH，
∴△CGE∽△AHE，
∴$\frac{CG}{AH}=\frac{EG}{EH}$。
∵CD = 2.8m，DF = 2m，
∴CG = CD - EF = 2.8 - 1.8 = 1(m)，EH = FD + BD = 2 + 20 = 22(m)，
∴$\frac{1}{AH}=\frac{2}{22}$，
∴AH = 11m，
∴AB = AH + HB = AH + EF = 11 + 1.8 = 12.8(m)。
答：醒狮雕塑 AB 的高度为 12.8m。

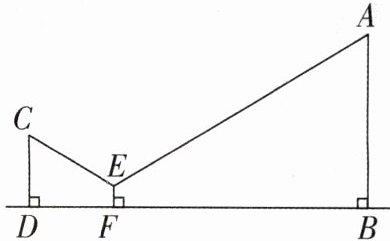
6 [2023 浙江湖州中考]某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点 F 处,再把镜子水平放在支架(EF)上的点 E 处,然后沿着直线 BF 后退至点 D 处,这时恰好在镜子里看到树的顶端 A,再用皮尺分别测量 BF,DF,EF,观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知 CD ⊥ BD 于点 D,EF ⊥ BD 于点 F,AB ⊥ BD 于点 B,BF = 6 米,DF = 2 米,EF = 0.5 米,CD = 1.7 米,则这棵树的高度(AB 的长)是______米.
]

答案：
4.1 【解析】过点 E 作水平线交 AB 于点 G，交 CD 于点 H，如图。
∵CD⊥DB，EF⊥DB，AB⊥DB，
∴DH = EF = GB = 0.5 米，EH = DF = 2 米，EG = FB = 6 米，
∴CH = CD - DH = 1.7 - 0.5 = 1.2(米)。根据题意，得∠CHE = ∠AGE = 90°，∠CEH = ∠AEG，
∴△CHE∽△AGE，
∴$\frac{EH}{EG}=\frac{CH}{AG}$，即$\frac{2}{6}=\frac{1.2}{AG}$，
∴AG = 3.6 米，
∴AB = AG + GB = 3.6 + 0.5 = 4.1(米)。故答案为 4.1°。