第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2025山西临汾曲沃期末,中]如图,在矩形ABCD中,AB= 5,CB= 12,连接AC,∠BAC的平分线交BC于点E,则线段BE的长为 ( )
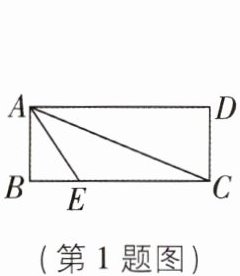
A.10/3
B.11/3
C.3
D.4

A.10/3
B.11/3
C.3
D.4
答案:
A
2[2025江苏泰州期中,中]如图,矩形ABCD的周长为24cm,两条对角线相交于点O,过点O作BD的垂线EF,分别交BC,AD于点E,F,连接BF,且AF= 3cm,则矩形ABCD的面积为 ( )
$A.24cm^2$
$B.28cm^2$
$C.32cm^2$
$D.36cm^2$
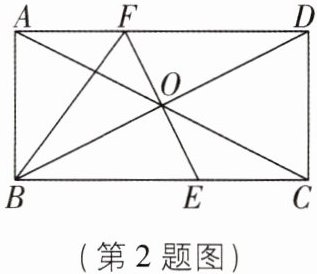
$A.24cm^2$
$B.28cm^2$
$C.32cm^2$
$D.36cm^2$

答案:
C
3[2024浙江杭州拱墅区调研,中]如图,矩形ABCD中,AC与BD相交于点O,AE平分∠BAD,若∠EAO= 15°,则∠AEO的度数为( )
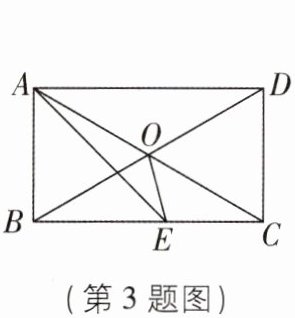
A.25°
B.30°
C.45°
D.60°

A.25°
B.30°
C.45°
D.60°
答案:
B
4[2025山西晋中质检,中]翻花绳是中国民间流传的儿童游戏,在中国不同的地域,有不同的称法,如线翻花、翻花鼓、挑绷绷、解股等等.翻花绳的一种图案可以抽象成如图所示的图形,在矩形ABCD中,IJ//KL,EF//GH,∠1= ∠2= 30°,∠3的度数为 ( )
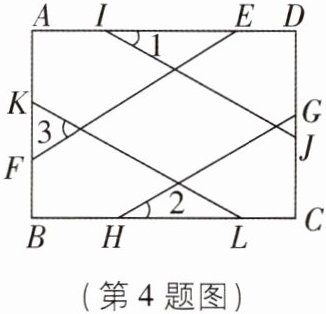
A.30°
B.45°
C.50°
D.60°

A.30°
B.45°
C.50°
D.60°
答案:
D
5[2024山东青岛调研,中]如图,在平面直角坐标系中,点O为坐标原点,将含30°角的Rt△ABC放在第一象限,其中30°角的对边BC长为1,斜边AB的端点A,B分别在y轴的正半轴、x轴的正半轴上滑动,连接OC,则线段OC的长的最大值是 ( )
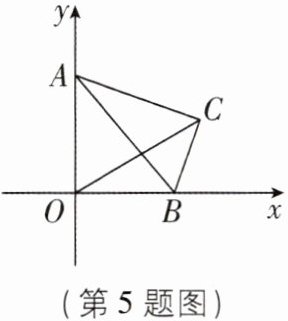
A.√5
B.√3
C.2
D.√7

A.√5
B.√3
C.2
D.√7
答案:
C
6[2025四川达州期末,中]如图,在矩形ABCD中,AB= 3,BC= 4,点M为AD的中点,点N为AB上一点,连接MN,CN,将△AMN沿直线MN折叠后,点A恰好落在CN上的点P处,则CN的长为______.
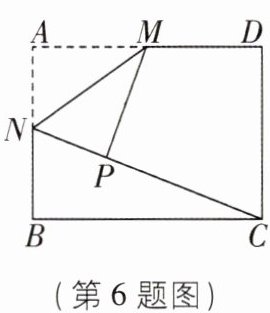

答案:
$\frac{13}{3}$
7[2024广东深圳质检,中]如图,以△ABC的边AB为对角线构造矩形ADBE,连接DE分别交AB,AC于点O,F,若F为AC中点,BD= 5,AD= BC= 12,则EF= ______.
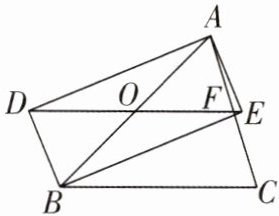

答案:
0.5
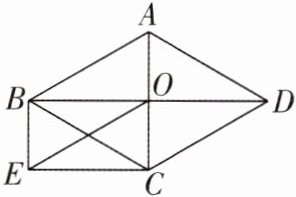
8[2024北京东城区期末,中]如图,四边形ABCD的对角线AC,BD相交于点O,BC,EO为矩形BECO对角线,BC//AD,AD= EO.
(1)求证:四边形ABCD是菱形;
(2)连接DE,若AC= 4,∠BCD= 120°,求DE的长.
(1)求证:四边形ABCD是菱形;
(2)连接DE,若AC= 4,∠BCD= 120°,求DE的长.

答案:
(1)【证明】
∵四边形BECO是矩形,
∴BC=EO,∠BOC=90°,
∴AC⊥BD.
∵AD=EO,
∴AD=BC.
∵BC//AD,
∴四边形ABCD是平行四边形.又
∵AC⊥BD,
∴四边形ABCD是菱形.
(2)【解】如图,
∵四边形ABCD是菱形,∠BCD=120°,
∴∠ABC=180° - 120°=60°,AB=BC,AO=CO=2,BO=DO,∠ABO=∠CBO,
∴△ABC是等边三角形,
∴AB=AC=4,
∴BO=$\sqrt{AB^2 - AO^2}$=$2\sqrt{3}$,
∴BD=$4\sqrt{3}$.
∵四边形BECO是矩形,
∴BE=CO=2,∠DBE=90°,
∴DE=$\sqrt{BD^2 + BE^2}$=$\sqrt{(4\sqrt{3})^2 + 2^2}$=$2\sqrt{13}$.
(1)【证明】
∵四边形BECO是矩形,
∴BC=EO,∠BOC=90°,
∴AC⊥BD.
∵AD=EO,
∴AD=BC.
∵BC//AD,
∴四边形ABCD是平行四边形.又
∵AC⊥BD,
∴四边形ABCD是菱形.
(2)【解】如图,
∵四边形ABCD是菱形,∠BCD=120°,
∴∠ABC=180° - 120°=60°,AB=BC,AO=CO=2,BO=DO,∠ABO=∠CBO,
∴△ABC是等边三角形,
∴AB=AC=4,
∴BO=$\sqrt{AB^2 - AO^2}$=$2\sqrt{3}$,
∴BD=$4\sqrt{3}$.
∵四边形BECO是矩形,
∴BE=CO=2,∠DBE=90°,
∴DE=$\sqrt{BD^2 + BE^2}$=$\sqrt{(4\sqrt{3})^2 + 2^2}$=$2\sqrt{13}$.
查看更多完整答案,请扫码查看


