《2025年初中必刷题九年级数学上册北师大版》

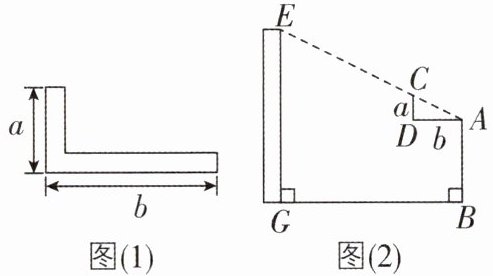
1 [中]西周数学家商高总结了用“矩”(如图(1))测量物高的方法:把“矩”水平放置在如图(2)所示的位置,从“矩”的一端 A(人眼)望点 E,使视线通过点 C,记人站立的位置为点 B,量出 BG 长,即可算得物高 EG.令 BG = x m,EG = y m,若 a = 30 cm,b = 60 cm,AB = 1.6 m,则 y 关于 x 的函数表达式为( )

A.$ y = \frac{1}{2}x $
B.$ y = \frac{1}{2}x + 1.6 $
C.$ y = 2x + 1.6 $
D.$ y = \frac{180}{x} + 1.6 $
]

答案： B 【解析】在题图
(2)中，延长 AD 交 EG 于点 F。由题意可得，AF = BG = x m，EF = EG - FG，FG = AB = 1.6m，EG = y m，
∴EF = (y - 1.6)m。
∵CD⊥AF，EF⊥AF，
∴CD//EF，
∴易证△ADC∽△AFE，
∴$\frac{CD}{EF}=\frac{AD}{AF}$，即$\frac{0.3}{EF}=\frac{0.6}{AF}$，
∴$\frac{0.3}{y - 1.6}=\frac{0.6}{x}$，化简，得$y = \frac{1}{2}x + 1.6$，故选 B。

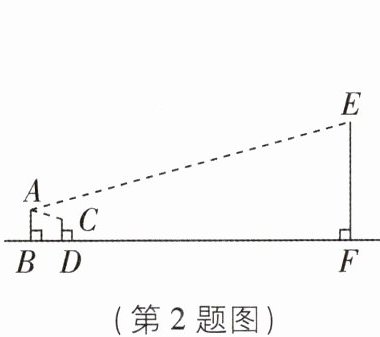
2 [2025 天津河西区质检,中]如图,小明在墙上挂了一面镜子 AB,调整好标杆 CD 的位置后,正好可以顺着标杆顶部在镜子上边缘 A 处看到旗杆的顶端 E,已知 AB = 2 m,CD = 1.5 m,BD = 2 m,BF = 20 m,则旗杆 EF 的高度为______m.

答案：
7 【解析】如图，C'，D'分别为点 C，D 关于 AB 的对称点，过 C'作 C'H//FD 分别交 AB，EF 于点 G，H；
∵EF//AB//C'D'，
∴易得四边形 C'D'BG，四边形 GBFH 是矩形，
∴HF = GB = C'D' = CD = 1.5m，C'G = D'B = BD = 2m，GH = BF = 20m，
∴C'H = 22m，AG = AB - GB = "2" - 1."5" = 0.5(m)．连接 AC'，则易得 C'，A，E 共线。
∵∠AC'G = ∠EC'H，∠AGC' = ∠EHC' = 90°，
∴△AC'G∽△EC'H，
∴$\frac{EH}{AG}=\frac{C'H}{C'G}$，
∴$\frac{EH}{0.5}=\frac{22}{2}$，
∴EH = 5.5m,
∴旗杆 EF 的高度为5.5 + 1.5 = 7(m)。

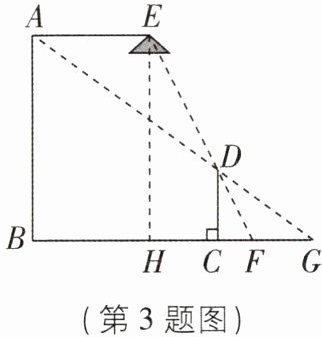
3 [2024 陕西宝鸡陈仓区期末,中]如图,AB 为路灯主杆,AE 为路灯的悬臂,CD 是长为 1.8 米的标杆.已知路灯悬臂 AE 与地面 BG 平行,当标杆竖立于地面时,主杆顶端 A、标杆顶端 D 和地面上一点 G 在同一直线上,此时小明发现路灯 E、标杆顶端 D 和地面上另一点 F 也在同一条直线上(路灯主杆底端 B、标杆底端 C 和地面上点 F、点 G 在同一水平线上).这时小明测得 FG 长 1.5 米,路灯的正下方 H 距离路灯主杆底端 B 的距离为 3 米,则路灯主杆 AB 的高度为______米.

答案：
5.4 【解析】如图，延长 AE，CD相交于点 N。
∵AE//BG，EH⊥BH，
∴易得四边形 AEHB 是矩形，
∴AE = BH = 3 米。
∵AE//BG，
∴易证△AED∽△GFD，△END∽△FCD，
∴$\frac{AE}{FG}=\frac{ED}{DF}=\frac{3}{1.5}=2$，
∴$\frac{ED}{DF}=\frac{DN}{CD}=2$。又
∵CD = 1.8 米，
∴DN = 1.8×2 = 3.6(米)，
∴AB = DN + CD = 3.6 + 1.8 = 5.4(米)。故答案为 5.4。
思路分析：延长 AD交 EG 于点 F，根据题意和图形，可以得到，AF = BG = x m，EF = EG - FG，FG = AB = 1.6m，EG = y m，然后根据相似三角形的判定和性质，可以得到 y 关于 x 的函数表达式。
关键点拨：延长 AE，CD 相交于点 N，构造△AED∽△GFD，△END∽△FCD 是解题 的关键。

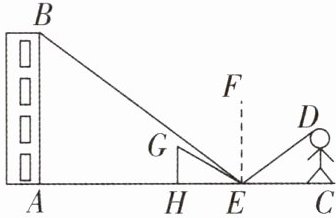
4 [中]小丽和小明想测量河对岸一建筑物的高度 AB.如图,他们先在地面上放一面平面镜 E,小丽在射线 AE 上调整自己与镜子的距离,直到刚好能从镜子中看到建筑物的顶端 B,此时她与镜子的距离 CE = 2 米,然后小明在距离建筑物 6 米处安装了一个测倾器 GH,测得∠HGE = 60°,若小丽的眼睛距离地面的高度 CD = 1.6 米,GH = 1 米,AB ⊥ AC,GH ⊥ AC,DC ⊥ AC,点 A,H,E,C 在同一条直线上.请你利用这些数据,求建筑物的高度 AB.(结果精确到 0.1 米,参考数据:$ \sqrt{2} \approx 1.414,\sqrt{3} \approx 1.732 $)
]

答案：
思路分析：相似三角形的应用，Rt△HEG 含 30°锐角，勾股定理 HE = $\sqrt{3}$，AE = AH + HE，AB = $\frac{AE\cdot CD}{CE}$，∠AEB = ∠CED，△ABE∽△CDE，$\frac{AB}{CD}=\frac{AE}{CE}$，∠BAE = ∠DCE。
【解】由题意得 AH = 6 米。
∵AB⊥AC，GH⊥AC，DC⊥AC，
∴∠BAE = ∠DCE = ∠GHE = 90°。在 Rt△GHE 中，∠HGE = 60°，GH = 1 米，
∴∠HEG = 30°，
∴GE = 2GH = 2 米，
∴EH = $\sqrt{2^2 - 1^2}=\sqrt{3}$(米)，
∴AE = AH + EH = (6 + $\sqrt{3}$)米。
∵∠AEB = ∠CED，∠BAE = ∠DCE = 90°，
∴△ABE∽△CDE，
∴$\frac{AB}{CD}=\frac{AE}{CE}$，即$\frac{AB}{1.6}=\frac{6 + \sqrt{3}}{2}$，
∴AB = 0.8(6 + $\sqrt{3}$)≈6.2(米)。
答：建筑物的高度 AB 约为 6.2 米。

5 核心素养 数学建模 [较难]学习了相似三角形相关知识后,小明和同学们想利用标杆测量大楼的高度.如图,小明站立在地面上的点 F 处,他的同学在点 B 处竖立标杆 AB,使得小明的头顶点 E、标杆顶点 A、大楼顶点 C 在一条直线上(点 F,B,D 也在一条直线上).已知小明的身高 EF = 1.5 米,标杆 AB = 2.5 米,且 BD = 23 米,FB = 2 米.
(1)求大楼的高度 CD 为多少米(CD 垂直于地面 BD).
(2)小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼 CD 上点 G 的高度 GD = 11.5 米,那么相对于第一次测量,标杆 AB 应该向大楼方向移动多少米?
]

答案：

(1)【解】如图
(1)，过点 E 作 EH⊥CD 于点 H，交 AB 于点 J，则四边形 EFBJ，四边形 EFDH 都是矩形。
∴EF = BJ = DH = 1.5 米，BF = EJ = 2 米，DB = JH = "23" 米。
∵AB = 2.5 米，
∴AJ = AB - BJ = 2.5 - 1.5 = 1(米)。
∵AJ//CH，
∴易得△EAJ∽△ECH，
∴$\frac{AJ}{CH}=\frac{EJ}{EH}$，
∴$\frac{1}{CH}=\frac{2}{2 + 23}$，
∴CH = 12.5 米，
∴CD = CH + DH = 12.5 + 1.5 = 14(米)。

(2)如图
(2)，过点 E 作 ET⊥CD 于点 T，交 AB 于点 R。设 BF = x 米。
∵AR//GT，
∴易得△ERA∽△ETG，
∴$\frac{AR}{GT}=\frac{ER}{ET}$，
∴$\frac{1}{11.5 - 1.5}=\frac{x}{2 + 23}$，
∴x = 2.5。
∵2.5 - 2 = 0.5(米)，
∴标杆 AB 应该向大楼方向移动 0.5 米。