第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
一、选择题(本大题共2小题,每小题12分,共24分)
1[2025广东深圳质检]2025第14届深圳国际导热散热材料及设备展览会将于2025年6月在深圳国际会展中心举办.若小张随机从A,B,C三个入口中选择一个进入,再随机从D,E两个出口中选择一个离开,则小张从B口进入,D口离开的概率是( )
A. $\frac{1}{6}$ B. $\frac{1}{5}$ C. $\frac{1}{4}$ D. $\frac{1}{3}$
2甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其他差异).从口袋中随机摸出两个小球,记下标号.若两个小球的标号之积为奇数,则甲获胜;若两个小球的标号之积为偶数,则乙获胜.乙获胜的概率是( )
A. $\frac{1}{12}$ B. $\frac{1}{6}$ C. $\frac{1}{2}$ D. $\frac{5}{6}$
1[2025广东深圳质检]2025第14届深圳国际导热散热材料及设备展览会将于2025年6月在深圳国际会展中心举办.若小张随机从A,B,C三个入口中选择一个进入,再随机从D,E两个出口中选择一个离开,则小张从B口进入,D口离开的概率是( )
A. $\frac{1}{6}$ B. $\frac{1}{5}$ C. $\frac{1}{4}$ D. $\frac{1}{3}$
2甲、乙两名同学玩一个游戏:在一个不透明的口袋中装有标号分别为1,2,3,4的四个小球(除标号外无其他差异).从口袋中随机摸出两个小球,记下标号.若两个小球的标号之积为奇数,则甲获胜;若两个小球的标号之积为偶数,则乙获胜.乙获胜的概率是( )
A. $\frac{1}{12}$ B. $\frac{1}{6}$ C. $\frac{1}{2}$ D. $\frac{5}{6}$
答案:
1.A 【解析】画树状图如下:

由树状图可知,共有6种等可能的结果,其中小张从 B 口进入,D 口离开的结果只有1种,
∴小张从 B 口进入,D 口离开的概率是$\frac {1}{6}$. 故选 A.
2.D 【解析】画树状图如下:

共有12种等可能的结果,其中两个小球的标号之积为偶数的结果有10种,
∴乙获胜的概率为$\frac {10}{12}=\frac {5}{6}$. 故选 D.
1.A 【解析】画树状图如下:

由树状图可知,共有6种等可能的结果,其中小张从 B 口进入,D 口离开的结果只有1种,
∴小张从 B 口进入,D 口离开的概率是$\frac {1}{6}$. 故选 A.
2.D 【解析】画树状图如下:

共有12种等可能的结果,其中两个小球的标号之积为偶数的结果有10种,
∴乙获胜的概率为$\frac {10}{12}=\frac {5}{6}$. 故选 D.
二、填空题(本大题共2小题,每小题12分,共24分)
3[2025江苏南京期末]在一个不透明的袋子中装有若干个白球和10个黑球,这些球除颜色外都相同.从袋中随机摸出一球,记下其颜色,这称为一次摸球试验.然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
|摸球试验次数|100|1000|5000|10000|50000|100000|
|摸出白球的次数|55|618|3032|5957|30104|59995|
|摸出白球的频率|0.550|0.618|0.606|0.596|0.602|0.600|
根据试验所得数据,估计白球有______个.
4一只不透明的袋子中装有1个黄球,现放入若干个红球,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,使得$P( )摸出一红一黄$)= P( )摸出两红$)$,则放入的红球个数为______.
3[2025江苏南京期末]在一个不透明的袋子中装有若干个白球和10个黑球,这些球除颜色外都相同.从袋中随机摸出一球,记下其颜色,这称为一次摸球试验.然后把它重新放回袋中并摇匀,不断重复上述过程.以下是利用计算机模拟的摸球试验统计表:
|摸球试验次数|100|1000|5000|10000|50000|100000|
|摸出白球的次数|55|618|3032|5957|30104|59995|
|摸出白球的频率|0.550|0.618|0.606|0.596|0.602|0.600|
根据试验所得数据,估计白球有______个.
4一只不透明的袋子中装有1个黄球,现放入若干个红球,它们与黄球除颜色外都相同,搅匀后从中任意摸出两个球,使得$P( )摸出一红一黄$)= P( )摸出两红$)$,则放入的红球个数为______.
答案:
3.15 【解析】观察题中表格发现随着摸球试验次数的增多,摸出白球的频率逐渐稳定在0.6附近,故摸出白球的概率估计值为0.6. 设白球有x个,则$\frac {x}{x+10}=0.6$,解得$x=15$,经检验,$x=15$是原方程的根,且符合题意,故答案为15.
4.3 【解析】假设袋中红球个数为1,此时袋中有1个黄球、1个红球,搅匀后从中任意摸出两个球,P(摸出一红一黄)=1,P(摸出两红)=0,不符合题意. 假设袋中的红球个数为2,画树状图如下:

由图可知,共有6种等可能的结果,其中摸到两个红球的结果有2种,摸出一红一黄的结果有4种,
∴P(摸出一红一黄)$=\frac {4}{6}=\frac {2}{3}$,P(摸出两红)$=\frac {2}{6}=\frac {1}{3}$,不符合题意. 假设袋中的红球个数为3,画树状图如下:

由图可知,共有12种等可能的结果,其中摸到两个红球的结果有6种,摸出一红一黄的结果有6种,
∴P(摸出一红一黄)=P(摸出两红)$=\frac {6}{12}=\frac {1}{2}$,符合题意,
∴放入的红球个数为3,故答案为3.
3.15 【解析】观察题中表格发现随着摸球试验次数的增多,摸出白球的频率逐渐稳定在0.6附近,故摸出白球的概率估计值为0.6. 设白球有x个,则$\frac {x}{x+10}=0.6$,解得$x=15$,经检验,$x=15$是原方程的根,且符合题意,故答案为15.
4.3 【解析】假设袋中红球个数为1,此时袋中有1个黄球、1个红球,搅匀后从中任意摸出两个球,P(摸出一红一黄)=1,P(摸出两红)=0,不符合题意. 假设袋中的红球个数为2,画树状图如下:

由图可知,共有6种等可能的结果,其中摸到两个红球的结果有2种,摸出一红一黄的结果有4种,
∴P(摸出一红一黄)$=\frac {4}{6}=\frac {2}{3}$,P(摸出两红)$=\frac {2}{6}=\frac {1}{3}$,不符合题意. 假设袋中的红球个数为3,画树状图如下:

由图可知,共有12种等可能的结果,其中摸到两个红球的结果有6种,摸出一红一黄的结果有6种,
∴P(摸出一红一黄)=P(摸出两红)$=\frac {6}{12}=\frac {1}{2}$,符合题意,
∴放入的红球个数为3,故答案为3.
三、解答题(本大题共2小题,共52分)
5[2024江苏南京秦淮区调研]将A、B、C三个完全一样的不透明杯子依次排成一排,倒扣在水平桌面上,其中一个杯子内有一枚硬币.
(1)若同时随机翻开两个杯子,请用画树状图或列表的方法求出现硬币的概率;
(2)若这枚硬币在A杯内,现从三个杯子中随机选择两个交换位置(硬币随A杯一起移动),则经过两次交换后,求硬币恰好在中间位置的杯子内的概率.
5[2024江苏南京秦淮区调研]将A、B、C三个完全一样的不透明杯子依次排成一排,倒扣在水平桌面上,其中一个杯子内有一枚硬币.
(1)若同时随机翻开两个杯子,请用画树状图或列表的方法求出现硬币的概率;
(2)若这枚硬币在A杯内,现从三个杯子中随机选择两个交换位置(硬币随A杯一起移动),则经过两次交换后,求硬币恰好在中间位置的杯子内的概率.
答案:
【解】
(1)假设硬币在 A 杯内,根据题意画树状图如下:

共有6种等可能的情况,其中出现硬币的情况有4种,则出现硬币的概率是$\frac {4}{6}=\frac {2}{3}.$
(2)根据题意得,第一次交换后的情况有BAC,CBA,ACB;把 BAC 再交换一次的情况有 ABC,CAB,BCA,把 CBA 再交换一次的情况有 BCA,ABC,CAB,把 ACB 再交换一次的情况有 CAB,BCA,ABC,则共有9种等可能的情况,硬币恰好在中间位置的杯子内的情况有3种,则硬币恰好在中间位置的杯子内的概率为$\frac {3}{9}=\frac {1}{3}.$
【解】
(1)假设硬币在 A 杯内,根据题意画树状图如下:

共有6种等可能的情况,其中出现硬币的情况有4种,则出现硬币的概率是$\frac {4}{6}=\frac {2}{3}.$
(2)根据题意得,第一次交换后的情况有BAC,CBA,ACB;把 BAC 再交换一次的情况有 ABC,CAB,BCA,把 CBA 再交换一次的情况有 BCA,ABC,CAB,把 ACB 再交换一次的情况有 CAB,BCA,ABC,则共有9种等可能的情况,硬币恰好在中间位置的杯子内的情况有3种,则硬币恰好在中间位置的杯子内的概率为$\frac {3}{9}=\frac {1}{3}.$
6某校为落实“双减”工作,增强课后服务的吸引力,充分用好课后服务时间,为学有余力的学生拓展学习空间,成立了5个活动小组(每位学生只能参加一个活动小组):A.音乐;B.体育;C.美术;D.阅读;E.人工智能.为了解学生对以上活动的参与情况,随机抽取部分学生进行了调查统计,并根据统计结果,绘制了如图所示的两幅不完整的统计图.
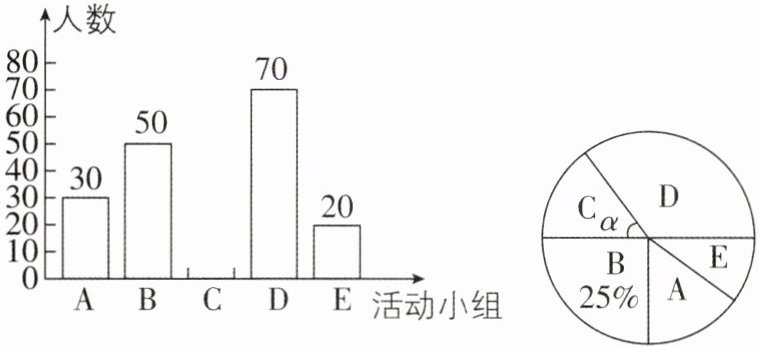
根据图中信息,解答下列问题:
(1)①此次调查一共随机抽取了______名学生;
②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角$\alpha =$______度.
(2)若该校有3200名学生,估计该校参加D组(阅读)的学生人数.
(3)刘老师计划从E组(人工智能)的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.

根据图中信息,解答下列问题:
(1)①此次调查一共随机抽取了______名学生;
②补全条形统计图(要求在条形图上方注明人数);
③扇形统计图中圆心角$\alpha =$______度.
(2)若该校有3200名学生,估计该校参加D组(阅读)的学生人数.
(3)刘老师计划从E组(人工智能)的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛,请用树状图法或列表法求出恰好抽中甲、乙两人的概率.
答案:
【解】
(1)①此次调查一共随机抽取的学生人数为$50÷25\% =200$. 故答案为 200.
②C 组的人数为$200-30-50-70-20=30.$
补全条形统计图如下:

③扇形统计图中圆心角$\alpha =360^{\circ }×\frac {30}{200}=54^{\circ },$故答案为 54.
(2)$3200×\frac {70}{200}=1120.$
答:估计该校参加D组(阅读)的学生人数为1120.
(3)画树状图如下:

共有12种等可能的结果,其中恰好抽中甲、乙两人的结果有2种,
∴恰好抽中甲、乙两人的概率为$\frac {2}{12}=\frac {1}{6}.$
【解】
(1)①此次调查一共随机抽取的学生人数为$50÷25\% =200$. 故答案为 200.
②C 组的人数为$200-30-50-70-20=30.$
补全条形统计图如下:

③扇形统计图中圆心角$\alpha =360^{\circ }×\frac {30}{200}=54^{\circ },$故答案为 54.
(2)$3200×\frac {70}{200}=1120.$
答:估计该校参加D组(阅读)的学生人数为1120.
(3)画树状图如下:

共有12种等可能的结果,其中恰好抽中甲、乙两人的结果有2种,
∴恰好抽中甲、乙两人的概率为$\frac {2}{12}=\frac {1}{6}.$
查看更多完整答案,请扫码查看


