第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2025陕西汉中校级质检]小明要用如图的两个转盘做“配紫色”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指(若指针指向分界线则重转)的颜色恰好配成紫色(红+蓝= 紫)的概率为( )

A.$\frac {1}{6}$
B.$\frac {1}{4}$
C.$\frac {1}{3}$
D.$\frac {1}{2}$

A.$\frac {1}{6}$
B.$\frac {1}{4}$
C.$\frac {1}{3}$
D.$\frac {1}{2}$
答案:
C 【解析】根据题意,列表如下:
白 蓝 红
红 (红,白) (红,蓝) (红,红)
蓝 (蓝,白) (蓝,蓝) (蓝,红)
共有6种等可能的结果,其中有2种结果可以配成紫色,故配成紫色の概率是$\frac{2}{6}=\frac{1}{3}$.故选C.
白 蓝 红
红 (红,白) (红,蓝) (红,红)
蓝 (蓝,白) (蓝,蓝) (蓝,红)
共有6种等可能的结果,其中有2种结果可以配成紫色,故配成紫色の概率是$\frac{2}{6}=\frac{1}{3}$.故选C.
2[2024江苏徐州鼓楼区调研]色光三原色(RGB)是指红、绿、蓝三色.把这三种色光按一定比例混合可以呈现各种色光.配色规律如图所示(例如:红光和蓝光按一定比例混合可以呈现紫光).
(1)从色光三原色中随机选择一种色光,选中红光的概率为____;
(2)甲、乙两位同学分别从色光三原色中随机选择一种色光进行混合,求可以呈现紫光的概率(用画树状图法或列表法).

(1)从色光三原色中随机选择一种色光,选中红光的概率为____;
(2)甲、乙两位同学分别从色光三原色中随机选择一种色光进行混合,求可以呈现紫光的概率(用画树状图法或列表法).

答案:
【解】
(1)从色光三原色中随机选择一种色光,选中红光的概率为$\frac{1}{3}$$,$故答案为$\frac{1}{3}$.
(2)列表如下:
甲 红 蓝 绿
乙
红 (红,红) (蓝,红) (绿,红)
蓝 (红,蓝) (蓝,蓝) (绿,蓝)
绿 (红,绿) (蓝,绿) (绿,绿)
由表知,共有9种等可能结果$,$其中可以呈现紫光的有2种结果$,$所以可以呈现紫光的概率为$\frac{2}{9}$.
(1)从色光三原色中随机选择一种色光,选中红光的概率为$\frac{1}{3}$$,$故答案为$\frac{1}{3}$.
(2)列表如下:
甲 红 蓝 绿
乙
红 (红,红) (蓝,红) (绿,红)
蓝 (红,蓝) (蓝,蓝) (绿,蓝)
绿 (红,绿) (蓝,绿) (绿,绿)
由表知,共有9种等可能结果$,$其中可以呈现紫光的有2种结果$,$所以可以呈现紫光的概率为$\frac{2}{9}$.
3如图是超市的两个摇奖转盘,只有当两个转盘指针同时指在偶数上时才能获一等奖,则摇奖人中一等奖的概率是( )

A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {1}{4}$
D.$\frac {1}{6}$

A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {1}{4}$
D.$\frac {1}{6}$
答案:
B 【解析】在第二个转盘中$,$4对应的圆心角度数是240°$,$相当于4出现两次$,$3出现一次$,$画树状图如图.由图可知$,$一共有6种゙等可能的情况$,$其中两次都是偶数の有2种情况$,$故摇奖人中一等奖の概率是$\frac{2}{6}=\frac{1}{3}$.故选B.

B 【解析】在第二个转盘中$,$4对应的圆心角度数是240°$,$相当于4出现两次$,$3出现一次$,$画树状图如图.由图可知$,$一共有6种゙等可能的情况$,$其中两次都是偶数の有2种情况$,$故摇奖人中一等奖の概率是$\frac{2}{6}=\frac{1}{3}$.故选B.

4[2025河南商丘质检]如图所示的两张扑克牌除正面图案外其他完全相同,将这两张扑克牌从正中间(沿图中虚线)剪断,得到四张形状大小相同的卡片(背面图案完全相同).将四张卡片洗匀后背面朝上,从中随机抽取一张,不放回,接着再随机抽取一张,则抽到的这两张卡片恰好能拼成一张完整扑克牌的概率是( )

A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {1}{4}$
D.$\frac {1}{6}$

A.$\frac {1}{2}$
B.$\frac {1}{3}$
C.$\frac {1}{4}$
D.$\frac {1}{6}$
答案:
B 【解析】将四张卡片分别记为A,B,C,D$,$其中A和B能拼成一张完整扑克牌$,$C和D能拼成一张完整扑克牌$,$画树状图如下:
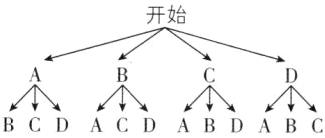
共有12种等可能的结果$,$其中抽到的这两张卡片恰好能拼成一张完整扑克牌的结果有AB,BA,CD,DC$,$共4种$,$
∴抽到的这两张卡片恰好能拼成一张完整扑克牌的概率为$\frac{4}{12}=\frac{1}{3}$.故选B.
B 【解析】将四张卡片分别记为A,B,C,D$,$其中A和B能拼成一张完整扑克牌$,$C和D能拼成一张完整扑克牌$,$画树状图如下:

共有12种等可能的结果$,$其中抽到的这两张卡片恰好能拼成一张完整扑克牌的结果有AB,BA,CD,DC$,$共4种$,$
∴抽到的这两张卡片恰好能拼成一张完整扑克牌的概率为$\frac{4}{12}=\frac{1}{3}$.故选B.
5[2025福建福州质检]某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.抽奖规则如下:
抽奖方案有以下两种:
方案A:从装有1个红球、2个白球(仅颜色不同)的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则没有奖金,兑奖后将摸出的球放回甲袋中;
方案B:从装有2个红球、1个白球(仅颜色不同)的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则没有奖金,兑奖后将摸出的球放回乙袋中.
抽奖条件是顾客购买商品的金额每满100元,可根据方案A抽奖一次,每满150元,可根据方案B抽奖一次(例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种:根据方案A抽奖三次或根据方案B抽奖两次或根据方案A,B各抽奖一次).
已知某顾客在该商场购买商品的金额为250元.
(1)若该顾客只选择根据方案A进行抽奖,求其所获奖金为15元的概率;
(2)以顾客所获得的奖金的平均值为依据,判断采用哪种方式抽奖更合算.
抽奖方案有以下两种:
方案A:从装有1个红球、2个白球(仅颜色不同)的甲袋中随机摸出1个球,若是红球,则获得奖金15元,否则没有奖金,兑奖后将摸出的球放回甲袋中;
方案B:从装有2个红球、1个白球(仅颜色不同)的乙袋中随机摸出1个球,若是红球,则获得奖金10元,否则没有奖金,兑奖后将摸出的球放回乙袋中.
抽奖条件是顾客购买商品的金额每满100元,可根据方案A抽奖一次,每满150元,可根据方案B抽奖一次(例如某顾客购买商品的金额为310元,则该顾客采用的抽奖方式可以有以下三种:根据方案A抽奖三次或根据方案B抽奖两次或根据方案A,B各抽奖一次).
已知某顾客在该商场购买商品的金额为250元.
(1)若该顾客只选择根据方案A进行抽奖,求其所获奖金为15元的概率;
(2)以顾客所获得的奖金的平均值为依据,判断采用哪种方式抽奖更合算.
答案:
【解】
(1)由于该顾客在该商场购买商品的金额为250元$,$只选择根据方案A进行抽奖$,$因此可以抽两次.由抽奖规则可知$,$两次摸球的结果为一红一白可获得奖金15元.从1个红球、2个白球中有放回地摸取两次$,$将2个白球分别记为白1$,$白2$,$所有可能出现的结果如下:
第一次 红 白1 白2
第二次
红 红,红 白1,红 白2,红
白1 红,白1 白1,白1 白2,白1
白2 红,白2 白1,白2 白2,白2
共有9种等可能出现的结果$,$其中结果为一红一白的有4种$,$所以该顾客只选择根据方案A进行抽奖$,$所获奖金为15元的概率为$\frac{4}{9}$.
(2)①由
(1)可得$,$只选择方案A抽奖两次$,$获得15元的概率为$\frac{4}{9}$$,$获得30元(结果为两次都是红球)的概率为$\frac{1}{9}$$,$两次都不获奖(结果为两次都是白球)的概率为$\frac{4}{9}$$,$所以只选择方案A进行抽奖获得奖金的平均值为$15×\frac{4}{9}+30×\frac{1}{9}+0×\frac{4}{9}=10$(元).
②选择方案A抽奖一次$,$方案B抽奖一次$,$所获奖金的平均值为$15×\frac{1}{3}+10×\frac{2}{3}\approx11.7$(元).因为10<11.7$,$所以选择方案A、方案B各抽奖一次更为合算.
(1)由于该顾客在该商场购买商品的金额为250元$,$只选择根据方案A进行抽奖$,$因此可以抽两次.由抽奖规则可知$,$两次摸球的结果为一红一白可获得奖金15元.从1个红球、2个白球中有放回地摸取两次$,$将2个白球分别记为白1$,$白2$,$所有可能出现的结果如下:
第一次 红 白1 白2
第二次
红 红,红 白1,红 白2,红
白1 红,白1 白1,白1 白2,白1
白2 红,白2 白1,白2 白2,白2
共有9种等可能出现的结果$,$其中结果为一红一白的有4种$,$所以该顾客只选择根据方案A进行抽奖$,$所获奖金为15元的概率为$\frac{4}{9}$.
(2)①由
(1)可得$,$只选择方案A抽奖两次$,$获得15元的概率为$\frac{4}{9}$$,$获得30元(结果为两次都是红球)的概率为$\frac{1}{9}$$,$两次都不获奖(结果为两次都是白球)的概率为$\frac{4}{9}$$,$所以只选择方案A进行抽奖获得奖金的平均值为$15×\frac{4}{9}+30×\frac{1}{9}+0×\frac{4}{9}=10$(元).
②选择方案A抽奖一次$,$方案B抽奖一次$,$所获奖金的平均值为$15×\frac{1}{3}+10×\frac{2}{3}\approx11.7$(元).因为10<11.7$,$所以选择方案A、方案B各抽奖一次更为合算.
查看更多完整答案,请扫码查看


