《2025年初中必刷题九年级数学上册北师大版》

1[2025重庆江北区质检]若$\triangle ABC$的三边长分别是3,5,6,则与$\triangle ABC相似的\triangle DEF$的三边长可能是( )

A.$DE= 6,DF= 8,EF= 10$
B.$DE= 9,EF= 18,DF= 25$
C.$DE= 1,EF= 2,DF= 2.5$
D.$DE= 6,DF= 10,EF= 12$

答案： D 【解析】
∵ DE=6,DF=8,EF=10,$\frac{3}{6} \neq$$\frac{5}{8} \neq \frac{6}{10}$,
∴ △ABC与△DEF不相似,故A不符合题意;
∵ DE=9,EF=18,DF=25,$\frac{3}{9} \neq \frac{5}{18} \neq$$\frac{6}{25}$,
∴ △ABC与△DEF不相似,故B不符合题意;
∵ DE=1,EF=2,DF=2.5,$\frac{3}{1} \neq \frac{5}{2} \neq \frac{6}{2.5}$,
∴ △ABC与△DEF不相似,故C不符合题意;
∵ DE=6,DF=10,EF=12,$\frac{3}{6}=\frac{5}{10}=\frac{6}{12}$,
∴ △ABC与△DEF相似,故D符合题意.故选D.

2在$\triangle ABC和\triangle DEF$中,已知$AB= AC,DE= DF$,如果从下列条件中增添一个条件,$\triangle ABC与\triangle DEF$仍不一定相似,那么这个条件是( )

A.$∠A= ∠D$
B.$∠B= ∠E$
C.$∠A= ∠E$
D.$\frac {AB}{BC}= \frac {DE}{EF}$

答案： C 【解析】A选项,由∠A=∠D,可以根据两边成比例且夹角相等,推出两三角形相似,本选项不符合题意;B选项,由∠B=∠E,可以推出∠A=∠D,根据两边成比例且夹角相等,推出两三角形相似,本选项不符合题意;C选项,由∠A=∠E,不能判定两三角形相似,本选项符合题意;D选项,由$\frac{AB}{BC}=\frac{DE}{EF}$,可以推出$\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}$,根据三边成比例推出两三角形相似,本选项不符合题意.故选C.

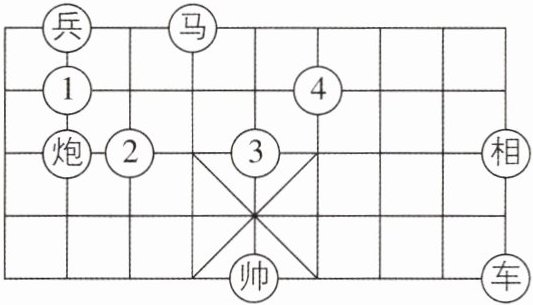
3新考向传统文化[2025山东济南期中]象棋是中国棋文化,也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.如图是象棋的棋盘局部(各个小正方形的边长均相等),根据“马走日”的规则,“马”应该落在位置____处,能使“马”“炮”“兵”所在位置的格点构成的三角形与“帅”“车”“相”所在位置的格点构成的三角形相似.
]

答案： ② 【解析】设棋盘中各个小正方形的边长均为1.由题图可知,“帅”“车”“相”所在位置的格点构成的三角形的三边长分别为4,2,$2\sqrt{5}$，“兵”“炮”所在位置的格点之间的距离为2，“炮”与②所在位置的格点之间的距离为1，“兵”与②所在位置的格点之间的距离为$\sqrt{5}$.
∵$\frac{4}{2}=\frac{2}{1}=\frac{2\sqrt{5}}{\sqrt{5}}=\frac{2}{1}$,
∴“马”应该落在位置②处,故答案为②.

4如图,已知O是$\triangle ABC$内一点,D,E,F分别是OA,OB,OC的中点.求证:$\triangle ABC\backsim \triangle DEF.$
]

答案： 【证明】
∵ D,E,F分别是OA,OB,OC的中点,
∴ DE=$\frac{1}{2}$AB,EF=$\frac{1}{2}$BC,DF=$\frac{1}{2}$AC,即$\frac{DE}{AB}=$$\frac{EF}{BC}=\frac{DF}{AC}$,
∴ △ABC∽△DEF.

5[2025广东广州校级质检]如图,四边形ABCD、四边形DCFE、四边形EFGH是边长相等的正方形,且点B,C,F,G在同一直线上,则$∠1+∠2$的度数为____.
]

答案： 45° 【解析】设正方形的边长为a.由勾股定理得$AC^2=a^2+a^2=2a^2$,
∴ AC=$\sqrt{2}a$.同理可得AF=$\sqrt{5}a$,AG=$\sqrt{10}a$.
∵$\frac{\sqrt{2}a}{2a}=\frac{a}{\sqrt{2}a}=\frac{\sqrt{5}a}{\sqrt{10}a}$,即$\frac{AC}{CG}=\frac{CF}{AC}=\frac{AF}{AG}$,
∴ △ACF∽△GCA,
∴ ∠2=∠CAF.
∵ ∠ACB=∠CAF+∠1=45°,
∴ ∠1+∠2=45°.

6如图,在四边形ABCD中,AC,BD相交于点F,点E在BD上,且$\frac {AB}{AE}= \frac {BC}{ED}= \frac {AC}{AD}.$
(1)$∠BAE与∠CAD$相等吗?为什么?
(2)试判断$\triangle ABE与\triangle ACD$是否相似,并说明理由.
]

答案： 【解】
(1)∠BAE与∠CAD相等.理由如下:
∵$\frac{AB}{AE}=\frac{BC}{ED}=\frac{AC}{AD}$,
∴ △ABC∽△AED,
∴ ∠BAC=∠EAD,
∴ ∠BAE=∠CAD.
(2)△ABE与△ACD相似.理由:
∵$\frac{AB}{AE}=\frac{AC}{AD}$,
∴$\frac{AB}{AC}=\frac{AE}{AD}$.在△ABE与△ACD中,$\frac{AB}{AC}=\frac{AE}{AD}$,∠BAE=∠CAD,
∴ △ABE∽△ACD.

7[2024河北石家庄期中]如图,正方形ABCD中,P是边BC上一点,$BE⊥AP,DF⊥AP$,垂足分别是点E,F,连接BF,如果$\frac {AF}{BF}= \frac {DF}{AD}$,求证:$EF= EP.$
]

答案：
【证明】如图,
∵ 四边形ABCD为正方形,
∴ AB=AD,∠BAD=90°.
∵ BE⊥AP,DF⊥AP,
∴ ∠BEA=∠AFD=90°,
∴ ∠1+∠2=∠2+∠3=90°,
∴ ∠1=∠3.在△ABE和△DAF中,$\left\{\begin{array}{l} ∠BEA=∠AFD,\\ ∠1=∠3,\\ AB=DA,\end{array}\right. $
∴ △ABE≌△DAF,
∴ BE=AF.又
∵$\frac{AF}{BF}=\frac{DF}{AD}$,
∴$\frac{BE}{BF}=\frac{DF}{AD}$,
∴$\frac{BE}{DF}=\frac{BF}{AD}$,
∴ 结合勾股定理易知$\frac{BE}{DF}=\frac{BF}{AD}=\frac{EF}{AF}$,
∴ △BEF∽△DFA,
∴ ∠4=∠3.又
∵ ∠1=∠3,
∴ ∠4=∠1.
∵ ∠1+∠APB=∠5+∠APB=90°,
∴ ∠5=∠1,
∴ ∠4=∠5,即BE平分∠FBP.
∵ BE⊥EP,
∴ 易得△BEP≌△BEF,
∴ EF=EP.

8如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的三边长分别是3,4,x,那么x的值为____.

答案： 5或$\sqrt{7}$ 【解析】根据题意,两条边长分别是6和8的直角三角形有两种情况,一种是6和8为直角边长,那么根据勾股定理可知斜边长为10;另一种是6时直角边长,8时斜边长,那么根据勾股定理可知另一条直角边长为$2\sqrt{7}$.所以另一个与它相似的直角三角形也两种情况,第一种是$\frac{6}{3}=\frac{8}{4}=\frac{10}{x}$,解得x=5;第二种是$\frac{6}{3}=\frac{2\sqrt{7}}{x}=\frac{8}{4}$,解得x=$\sqrt{7}$.综上,x=5或$\sqrt{7}$.