《2025年初中必刷题九年级数学上册北师大版》

1 [2024 甘肃临夏州中考]如图,$O$是坐标原点,菱形$ABOC的顶点B在x$轴的负半轴上,顶点$C的坐标为(3,4)$,则顶点$A$的坐标为( )

A.$(-4,2)$
B.$(-\sqrt{3},4)$
C.$(-2,4)$
D.$(-4,\sqrt{3})$

答案： C 【解析】如图，过 C 作 CN⊥x 轴于 N，过 A 作 AM⊥x 轴于 M.
∵ 点 C 的坐标为(3,4)，
∴ ON = 3，CN = 4，
∴ OC = √(ON²+CN²) = 5.
∵ 四边形 ABOC 是菱形，
∴ AC = OC = 5，AC//BO，
∴ 点 A 的坐标为(-2,4).故选 C.

2 [2024 四川泸州中考]已知四边形$ABCD$是平行四边形,下列条件中,不能判定$□ ABCD$为矩形的是( )

A.$∠A = 90^{\circ}$
B.$∠B = ∠C$
C.$AC = BD$
D.$AC⊥BD$

答案： D 【解析】
∵ 四边形 ABCD 是平行四边形，
∴ 当∠A = 90°时，平行四边形 ABCD 是矩形，故选项 A 不符合题意.
∵ 四边形 ABCD 是平行四边形，
∴ AB//CD，
∴ ∠B + ∠C = 180°.当∠B = ∠C 时，∠B = ∠C = 90°，
∴ □ABCD 为矩形，故选项 B 不符合题意.
∵ 四边形 ABCD 是平行四边形，
∴ 当 AC = BD 时，平行四边形 ABCD 是矩形，故选项 C 不符合题意.
∵ 四边形 ABCD 是平行四边形，
∴ 当 AC⊥BD 时，平行四边形 ABCD 是菱形，故选项 D 符合题意.故选 D.

3 如图,在$Rt\triangle ABC$中,$AB = 4$,点$M是斜边BC$的中点,以$AM为边作正方形AMEF$。若$S_{正方形AMEF} = 16$,则$S_{\triangle ABC} = $( )

A.$4\sqrt{3}$
B.$8\sqrt{3}$
C.12
D.16

答案： B 【解析】
∵ S_正方形AMEF = 16，
∴ AM = 4.
∵ M 是斜边 BC 的中点，
∴ BC = 2AM = 8，
∴ AC = √(BC² - AB²) = √(8² - 4²) = 4√3，
∴ S_△ABC = 1/2 AB·AC = 8√3.故选 B.

4 [2024 重庆沙坪坝区质检]如图,正方形$ABCD的对角线相交于点O$,点$E在AB$边上,点$F在OD$上,过点$E作EG⊥BD$,垂足为点$G$,若$FE = FC$,$EF⊥CF$,$OF = 3$,则$BE$的长为( )

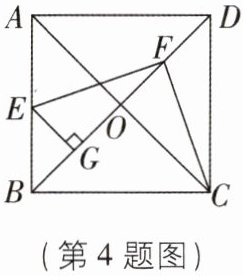
A.3
B.$3\sqrt{2}$
C.$3\sqrt{3}$
D.$2\sqrt{3}$

答案： B 【解析】
∵ 四边形 ABCD 是正方形，
∴ AC⊥BD，∠ABD = 45°.
∵ EF⊥CF，
∴ ∠COF = ∠EFC = 90°，
∴ ∠EFG = 90° - ∠CFO = ∠FCO.
∵ EG⊥BD，
∴ ∠EGF = ∠FOC = 90°.在△EFG 和△FCO 中，{∠EGF=∠FOC，∠EFG=∠FCO，FE=CF，
∴ △EFG≌△FCO(AAS)，
∴ EG = OF = 3.
∵ ∠ABD = 45°，
∴ △EBG 是等腰直角三角形，
∴ BE = √2 EG = 3√2，故选 B.

5 如图,在矩形$ABCD$中,$AB = 2$,$AD = 1$,$E为AB$的中点,$F为EC$上一动点,$P为DF$中点,连接$PB$,$DE$,则$PB$的最小值是( )

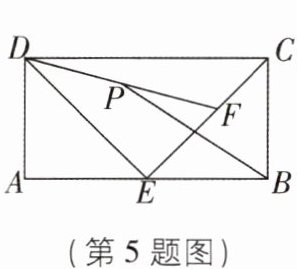
A.2
B.4
C.$\sqrt{2}$
D.$2\sqrt{2}$

答案： C 【解析】如图，当点 F 与点 C 重合时，点 P 在 P₁ 处，CP₁ = DP₁，当点 F 与点 E 重合时，点 P 在 P₂ 处，EP₂ = DP₂，
∴ 点 P 的运动轨迹是线段 P₁P₂，
∴ 当 BP⊥P₁P₂ 时，PB 取得最小值，此时垂足为 P₁，
∴ BP 的最小值为 BP₁ 的长.
∵ CP₁ = BC = 1，∠BCP₁ = 90°，
∴ BP₁ = √2，
∴ PB 的最小值√2.故选 C.

6 [2024 辽宁锦州期中]如图,在菱形$ABCD$中,$∠ABC = 60^{\circ}$,对角线$AC$,$BD相交于点O$,$P是对角线BD$上的一动点,且$PM⊥AB于点M$,$PN⊥AD于点N$。有以下结论：①$\triangle ABC$为等边三角形；②$OB = \sqrt{3}OA$；③$∠MPN = 60^{\circ}$；④$PM + PN = \frac{1}{2}BD$。其中正确的有( )

A.1 个
B.2 个
C.3 个
D.4 个

答案： D 【解析】
∵ 四边形 ABCD 是菱形，
∴ AB = BC.又
∵ ∠ABC = 60°，
∴ △ABC 为等边三角形①正确.
∵ 四边形 ABCD 是菱形，
∴ AC⊥BD，∠ABO = ∠CBO = 30°，
∴ OB = √3 OA，故 ② 正确.
∵ PM⊥AB，PN⊥AD，
∴ ∠AMP = ∠ANP = 90°.
∵ AD//BC，∠ABC = 60°，
∴ ∠BAD = 120°，
∴ ∠MPN = 60°，故③正确.如图，延长 NP 交 BC 于点 G.
∵ AD//BC，PN⊥AD，
∴ PG⊥BC.
∵ PM⊥AB，BP 平分∠ABC，
∴ PM = PG，
∴ PM + PN = PG + PN = NG.
∵ AD//BC，
∴ ∠PBG = ∠PDN = 30°，
∴ PB = 2PG，PD = 2PN，
∴ PM + PN = PG + PN = 1/2 PB + 1/2 PD = 1/2(PB + PD) = 1/2 BD，
∴ PM + PN = 1/2 BD，故④正确.综上所述，正确的有 4 个.故选 D.

7 如图,在平行四边形$ABCD$中,$AD = 2AB = 2$,$∠ABC = 60^{\circ}$,$E$,$F是对角线BD$上的动点,且$BE = DF$,$M$,$N分别是边AD$,边$BC$上的动点。下列说法：①存在无数个平行四边形$MENF$；②存在无数个矩形$MENF$；③存在无数个菱形$MENF$；④存在无数个正方形$MENF$。其中正确的个数是( )

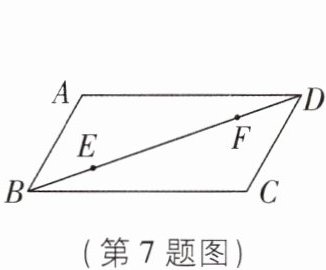
A.1
B.2
C.3
D.4

答案： C 【解析】如图，连接 AC，MN，ME，MF，NE，NF，且令 AC，MN，BD 相交于点 O.
∵ 四边形 ABCD 是平行四边形，
∴ OA = OC，OB = OD.
∵ BE = DF，
∴ OE = OF，
∴ 只要 OM = ON，那么四边形 MENF 就是平行四边形.
∵ 点 E，F 是 BD 上的动点，
∴ 存在无数个平行四边形 MENF，故①正确.只要 MN = EF，OM = ON，那么四边形 MENF 就是矩形.
∵ 点 E，F 是 BD 上的动点，
∴ 存在无数个矩形 MENF，故②正确.只要 MN⊥EF，OM = ON，那么四边形 MENF 就是菱形.
∵ 点 E，F 是 BD 上的动点，
∴ 存在无数个菱形 MENF，故③正确.只要 MN = EF，MN⊥EF，OM = ON，那么四边形 MENF 就是正方形，而符合要求的正方形只有一个，故④错误.故选 C.

8 [2025 山西太原质检]如图,矩形$ABCD$为一个正在倒水的水杯截面图,若杯内水面刚好经过点$D(DE// CF)$,且$∠AED = 50^{\circ}$,则水杯底面$BC与水平面夹角∠BCF$的大小为____。

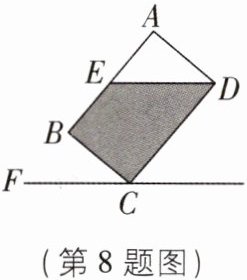
答案： 40° 【解析】延长 AB 交 CF 于点 G，如图所示.
∵ DE//CF，∠AED = 50°，
∴ ∠AGC = ∠AED = 50°.
∵ 四边形 ABCD 为矩形，
∴ ∠ABC = 90°，
∴ ∠CBG = 180° - ∠ABC = 90°，
∴ ∠BCF = 90° - 50° = 40°.故答案为 40°.

9 如图,菱形$ABCD的对角线AC$,$BD相交于点O$,点$E在OB$上,连接$AE$,点$F为CD$的中点,连接$OF$。若$AE = BE$,$OE = 3$,$OA = 4$,则线段$OF$的长为____。

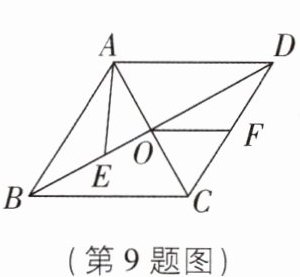
答案： 2√5 【解析】
∵ 四边形 ABCD 是菱形，
∴ AC⊥BD，AO = CO = 4，BO = DO，
∴ AE = √(AO² + EO²) = √(16 + 9) = 5，
∴ BE = AE = 5，
∴ BO = 8，
∴ BC = √(BO² + CO²) = √(64 + 16) = 4√5.
∵ 点 F 为 CD 的中点，BO = DO，
∴ OF = 1/2 BC = 2√5，故答案为 2√5.