《2025年初中必刷题九年级数学上册北师大版》

1 [2025 山西晋中期中]如图,小明在练习本上画出直线 $ a // b // c $,直线 $ m $,$ n $ 分别与直线 $ a $,$ b $,$ c $ 交于点 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $,则下列比例式错误的是( )

A.$ \frac { A B } { A C } = \frac { D E } { D F } $
B.$ \frac { A B } { B C } = \frac { D E } { E F } $
C.$ \frac { A D } { B E } = \frac { B E } { C F } $
D.$ \frac { B C } { E F } = \frac { A C } { D F } $

答案： C　[解析]
∵a//b//c，
∴$\frac{AB}{AC}=\frac{DE}{DF}$，故A不符合题意；
∵a//b//c，
∴$\frac{AB}{BC}=\frac{DE}{EF}$，故B不符合题意；
∵线段AD，BE，CF不是直线m，n上被截的线段，
∴$\frac{AD}{BE}$与$\frac{BE}{CF}$不一定相等，故C符合题意；
∵a//b//c，
∴$\frac{BC}{EF}=\frac{AC}{DF}$，故D不符合题意.故选C.

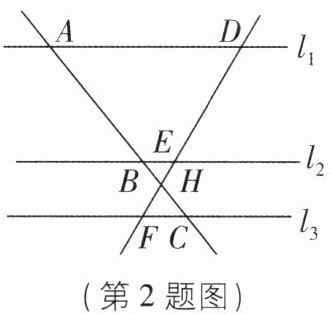
2 [2025 四川广安校级质检]如图,直线 $ l _ { 1 } // l _ { 2 } // l _ { 3 } $,直线 $ A C $ 分别交 $ l _ { 1 } $,$ l _ { 2 } $,$ l _ { 3 } $ 于点 $ A $,$ B $,$ C $,直线 $ D F $ 分别交 $ l _ { 1 } $,$ l _ { 2 } $,$ l _ { 3 } $ 于点 $ D $,$ E $,$ F $,$ A C $ 与 $ D F $ 相交于点 $ H $。如果 $ A B = 5 $,$ B H = 1 $,$ C H = 2 $,那么 $ \frac { E F } { D E } $ 的值等于( )

A.$ \frac { 1 } { 5 } $
B.$ \frac { 1 } { 3 } $
C.$ \frac { 2 } { 5 } $
D.$ \frac { 3 } { 5 } $

答案： D　[解析]
∵直线$l_1// l_2// l_3$，
∴$\frac{DE}{EF}=\frac{AB}{BC}$.
∵AB = 5，BH = 1，CH = 2，
∴BC = BH + CH = 3，
∴$\frac{BC}{AB}=\frac{3}{5}$，
∴$\frac{EF}{DE}=\frac{3}{5}$. 故选D.

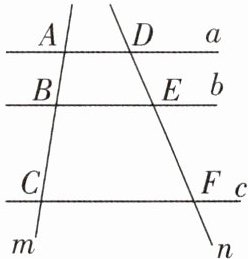
3 如图,直线 $ a // b // c $,直线 $ m $,$ n $ 与 $ a $,$ b $,$ c $ 分别相交于点 $ A $,$ B $,$ C $ 和点 $ D $,$ E $,$ F $。
(1)若 $ A B = 3 $,$ B C = 5 $,$ D E = 4 $,求 $ E F $ 的长。
(2)若 $ A B : B C = 2 : 5 $,$ D F = 10 $,求 $ E F $ 的长。
]

答案： 3.【解】
(1)
∵a//b//c，
∴$\frac{AB}{BC}=\frac{DE}{EF}$，即$\frac{3}{5}=\frac{4}{EF}$，解得$EF=\frac{20}{3}$.
(2)
∵a//b//c，
∴$\frac{AB}{BC}=\frac{DE}{EF}=\frac{2}{5}$，
∴$\frac{DE + EF}{EF}=\frac{2 + 5}{5}$，即$\frac{DF}{EF}=\frac{2 + 5}{5}$，解得$EF=\frac{50}{7}$.
本题容易因忽视a + b + c = 0的情况漏解，易错警示运用平行线分线段成比例的基本事实的推论时，一定要找准线段的对应关系.
刷有所得：运用平行线分线段成比例的基本事实求线段长的方法：先确定图形中的平行线，由此确定平行线截得的线段间的比例关系，得出含有待求线段的比例式，将已知线段的长度代入比例式中，进而可得出待求线段的长.

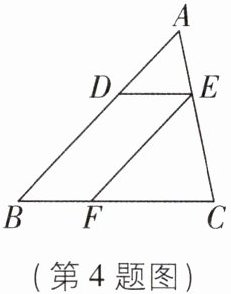
4 如图,已知在 $ \triangle A B C $ 中,点 $ D $,$ E $,$ F $ 分别是边 $ A B $,$ A C $,$ B C $ 上的点,$ D E // B C $,$ E F // A B $,且 $ A D : D B = 3 : 5 $,则 $ C F : C B = $( )

A.$ 5 : 8 $
B.$ 3 : 8 $
C.$ 3 : 5 $
D.$ 2 : 5 $

答案： A　[解析]
∵DE//BC，
∴AB∶DB = AC∶EC.
∵AD∶DB = 3∶5，
∴AB∶DB = 8∶5，
∴AC∶EC = 8∶5.
∵EF//AB，
∴CF∶CB = CE∶CA = 5∶8. 故选A.

5 如图,已知 $ A B // C D $,$ A D $ 与 $ B C $ 相交于点 $ O $。若 $ \frac { B O } { O C } = \frac { 2 } { 3 } $,$ A D = 10 $,则 $ A O = $____。

答案： 4　[解析]
∵AB//CD，
∴$\frac{AO}{OD}=\frac{BO}{OC}=\frac{2}{3}$，
∴$\frac{AO}{AD}=\frac{2}{5}$. 又
∵AD = 10，
∴AO = 4.

6 [2025 吉林长春质检]如图,五线谱是一种记谱法,通过在五条等距离的平行线上标以不同时值的音符及其他记号来记载音乐。同一条直线上的三个点 $ A $,$ B $,$ C $ 分别在五线谱的三条平行线上,若线段 $ B C = 4 \mathrm { cm } $,则线段 $ A C $ 的长是____。
]

答案：
6 cm　[解析]如图，过点A作平行横线的垂线，交点B所在的平行横线于D，交点C所在的平行横线于E，
∴$\frac{AB}{BC}=\frac{AD}{DE}$，即$\frac{AB}{4}=\frac{1}{2}$，解得AB = 2，
∴AC = 2 + 4 = 6(cm). 故答案为6 cm.

7 如图,已知 $ D E // B C $,$ F E // C D $,$ A F = 3 $,$ A D = 5 $,$ A E = 4 $。
(1)求 $ C E $ 的长；
(2)求 $ A B $ 的长。
]

答案： 7.【解】
(1)
∵FE//CD，
∴$\frac{AE}{AC}=\frac{AF}{AD}$，即$\frac{4}{AC}=\frac{3}{5}$，解得$AC=\frac{20}{3}$，则$CE = AC - AE=\frac{20}{3}-4=\frac{8}{3}$.
(2)
∵DE//BC，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，即$\frac{5}{AB}=\frac{4}{\frac{20}{3}}$，解得$AB=\frac{25}{3}$.

8 如图,在 $ \triangle A B C $ 中,点 $ D $,$ E $ 分别在 $ A B $,$ A C $ 上,$ D E // B C $,下列比例式中,不正确的是( )

A.$ \frac { A D } { A B } = \frac { A E } { A C } $
B.$ \frac { A D } { D B } = \frac { A E } { E C } $
C.$ \frac { A B } { A C } = \frac { A E } { A D } $
D.$ \frac { A D } { A E } = \frac { D B } { E C } $
]

答案： C　[解析]
∵DE//BC，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，$\frac{AD}{DB}=\frac{AE}{EC}$，$\frac{AB}{AC}=\frac{AD}{AE}$，$\frac{AD}{AE}=\frac{BD}{EC}$.
∴选项A、B、D均正确，选项C错误. 故选C.