《2025年初中必刷题九年级数学上册北师大版》

1 [2025江苏南京质检]如图,四边形ABCD的对角线AC,BD相交于O,且将这个四边形分成①②③④四个三角形,若OA：OC= OB：OD,则下列结论正确的是( )

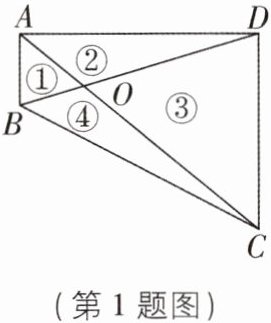
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似

答案： B 【解析】
∵ 四边形ABCD的对角线AC,BD相交于O，
∴ ∠AOB = ∠COD. 又
∵ OA:OC = OB:OD，
∴ △AOB∽△COD，即①和③相似. 故选B.

2 [2025山东淄博校级调研]如图,点D,E分别在△ABC的边AB,AC上,下列条件：①∠ADE= ∠C；②$\frac{AE}{AB}= \frac{DE}{BC}$；③$\frac{AD}{AC}= \frac{AE}{AB}$,其中使△ADE与△ACB一定相似的是( )

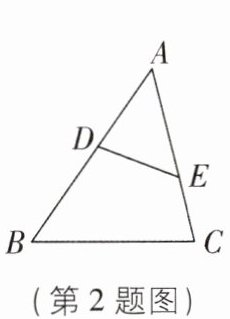
A.①②
B.②③
C.①③
D.①②③

答案： C 【解析】在△ADE和△ACB中，∠DAE = ∠CAB，若添加条件①∠ADE = ∠C，则根据“两角分别相等的两个三角形相似”可判定△ADE∽△ACB，①正确；若添加条件②$\frac{AE}{AB}=\frac{DE}{BC}$，则无法判定△ADE与△ACB相似，②错误；若添加条件③$\frac{AD}{AC}=\frac{AE}{AB}$，则根据“两边成比例且夹角相等的两个三角形相似”可判定△ADE∽△ACB，③正确。 故选C。

3 [2024湖南娄底期末]如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )

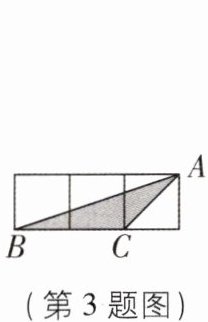
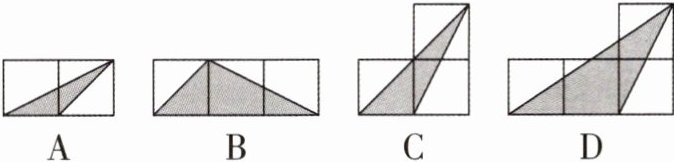
答案： A 【解析】在△ABC中，∠ACB = 135°，AC = $\sqrt{2}$，BC = 2。B、C、D选项中的三角形都没有135°的角，而A选项中，三角形的钝角为135°，钝角的两边长分别为1和$\sqrt{2}$，因为$\frac{2}{\sqrt{2}}=\frac{\sqrt{2}}{1}$，所以A选项中的三角形与△ABC相似。 故选A。

4 在△ABC和△DEF中,∠A= ∠D= 105°,AC= 4cm,AB= 6cm,DE= 3cm,则DF= ______时,△ABC与△DEF相似。

答案： 2 cm或4.5 cm 【解析】
∵ ∠A = ∠D，AB = 6 cm，AC = 4 cm，DE = 3 cm，
∴ 当$\frac{AB}{DE}=\frac{AC}{DF}$，即$\frac{6}{3}=\frac{4}{DF}$时，△ABC∽△DEF，解得DF = 2；当$\frac{AB}{DF}=\frac{AC}{DE}$，即$\frac{6}{DF}=\frac{4}{3}$时，△ABC∽△DFE，解得DF = 4.5。 综上所述，当DF = 2 cm或4.5 cm时，△ABC和△DEF相似。 故答案为2 cm或4.5 cm。

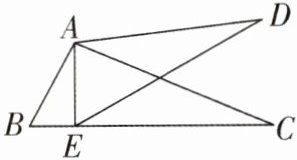
5 如图,E是△ABC的边BC上的点,已知∠BAE= ∠CAD,$\frac{AC}{AD}= \frac{6}{5}$,AB= 18,AE= 15。求证：△ABC∽△AED。

答案： 【证明】
∵ AB = 18，AE = 15，
∴ $\frac{AB}{AE}=\frac{18}{15}=\frac{6}{5}=\frac{AC}{AD}$。 又
∵ ∠BAE = ∠CAD，
∴ ∠BAE + ∠CAE = ∠CAD + ∠EAC，即∠BAC = ∠EAD，
∴ △ABC∽△AED。

6 在△ABC和△DEF中,∠A= 40°,∠D= 60°,∠E= 80°,$\frac{AB}{AC}= \frac{FD}{FE}$,那么∠B的度数是( )

A.40°
B.60°
C.80°
D.100°

答案： B 【解析】
∵ ∠D = 60°，∠E = 80°，
∴ ∠F = 40°，
∴ ∠F = ∠A。
∵ $\frac{AB}{AC}=\frac{FD}{FE}$，
∴ △BCA∽△DEF，
∴ ∠B与∠D是对应角，
∴ ∠B = ∠D = 60°。 故选B。

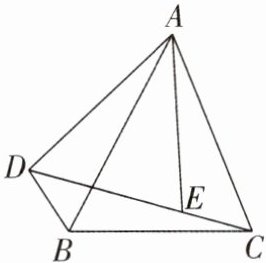
7 [2024安徽合肥蜀山区期中]如图,点D是△ABC外一点,连接DC,E是线段CD上一点,∠DAE= ∠BAC,∠AEC+∠ACB= 180°。求证：△DAB∽△EAC。

答案： 【证明】
∵ ∠AEC + ∠ACB = 180°，∠AEC + ∠AED = 180°，
∴ ∠AED = ∠ACB。
∵ ∠DAE = ∠BAC，
∴ △ADE∽△ABC，
∴ $\frac{AD}{AB}=\frac{AE}{AC}$，
∴ $\frac{AD}{AE}=\frac{AB}{AC}$。
∵ ∠DAE = ∠BAC，即∠DAB + ∠BAE = ∠BAE + ∠EAC，
∴ ∠DAB = ∠EAC，
∴ △DAB∽△EAC。

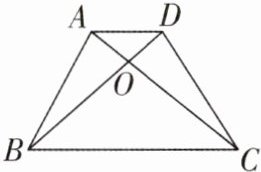
8 老师上完“相似三角形的判定”一课后,出了如下一道思考题：如图,在四边形ABCD中,AD//BC,对角线AC,BD相交于点O,△AOB和△DOC是否相似？
某学生的解答过程：△AOB∽△DOC。理由：在△AOB和△DOC中,∵AD//BC,∴易证△AOD∽△COB,∴$\frac{AO}{OC}= \frac{OD}{OB}$。又∵∠AOB= ∠DOC,∴△AOB∽△DOC。该学生的解答是否正确？若不正确,请说明理由。

答案： 【解】该学生的解答不正确。 △AOB与△DOC不相似。 理由如下：
∵ AD//BC，
∴ 易证△AOD∽△COB，
∴ $\frac{AO}{OC}=\frac{OD}{OB}$。 在△AOB和△DOC中，虽然∠AOB = ∠DOC，但是OA，OC不是夹∠AOB的两边，OD，OB也不是夹∠DOC的两边，
∴ △AOB与△DOC不相似。