《2025年初中必刷题九年级数学上册北师大版》

1 [2024 河北衡水冀州区期末,中]如图,平行四边形 ABCD 中,$∠A= 110^{\circ },AD= DC$.E,F 分别是边 AB 和 BC 的中点,$EP⊥CD$于点 P,连接 PF,EF,则$∠PEF= $( )

A.$35^{\circ }$
B.$45^{\circ }$
C.$50^{\circ }$
D.$55^{\circ }$

答案： A 【解析】
∵ 平行四边形ABCD中，AD=DC，
∴ 四边形ABCD为菱形，
∴ AB=BC，∠ABC=180°-∠A=70°.
∵ E，F 分别为 AB，BC 的中点，
∴ BE=BF，
∴ ∠BEF=∠BFE=$\frac{1}{2}$×(180°-70°)=55°.
∵ PE⊥CD，AB//CD，
∴ PE⊥AB，
∴ ∠PEB=90°，
∴ ∠PEF=90°-55°=35°，故选 A.

2 [2024 湖北武汉调研,较难]如图,在菱形 ABCD 中,$∠BAD= 60^{\circ }$,AC 与 BD 交于点 O,E 为 CD 延长线上的一点,且$CD= DE$,连接 BE 分别交 AC,AD 于点 F,G,连接 OG,则下列结论中一定成立的是( )
①$OG= \frac {1}{2}AB$;②与$\triangle DEG$全等的三角形共有 5 个;③四边形 ODEG 与四边形 OBAG 面积相等;④以 A,B,D,E 为顶点的四边形是菱形.

A.①③④
B.①④
C.①②③
D.②③④

答案： A 【解析】
∵ 四边形ABCD是菱形，
∴ AB=BC=CD=DA，AB//CD，OA=OC，OB=OD，AC⊥BD，
∴ ∠BAG=∠EDG，△ABO≌△CBO≌△CDO≌△ADO.
∵ CD=DE，
∴ AB=DE.在△ABG 和 △DEG 中，$\left\{\begin{array}{l} ∠BAG=∠EDG,\\ ∠AGB=∠DGE,\\ AB=DE,\end{array}\right. $
∴ △ABG≌△DEG(AAS)，
∴ AG=DG，
∴ OG 是△ACD 的中位线，
∴ OG=$\frac{1}{2}$CD=$\frac{1}{2}$AB，故①正确.连接 AE.
∵ AB//CE，AB=DE，
∴ 四边形 ABDE 是平行四边形.
∵ ∠BCD=∠BAD=60°，
∴ △ABD，△BCD 是等边三角形，
∴ AB=BD=AD，∠ODC=60°，
∴ OD=AG，四边形 ABDE 是菱形，故④正确.
∴ AD⊥BE，由菱形的性质得△ABG≌△DBG≌△DEG.在△ABG 和 △DCO 中，$\left\{\begin{array}{l} AG=OD,\\ ∠BAG=∠ODC=60°,\\ AB=DC,\end{array}\right. $
∴ △ABG≌△DCO（SAS），
∴ △ABO≌△CBO≌△CDO≌△ADO≌△BAG≌△BDG≌△EDG，
∴ 与△DEG 全等的三角形有 6 个，故②不正确.
∵ OB=OD，
∴ S△BOG=S△DOG.
∵ 四边形 ABDE 是菱形，
∴ S△ABG=S△DGE，
∴ 四边形 ODEG 与四边形 OBAG 面积相等，故③正确.故选 A.

3 [中]如图,$\triangle ABC$是边长为 1 的等边三角形,分别取 AC,BC 边的中点 D,E,连接 DE,作$EF// AC$得到四边形 EDAF,它的周长记作$C_{1}$;分别取 EF,BE 的中点$D_{1},E_{1}$,连接$D_{1}E_{1}$,作$E_{1}F_{1}// EF$,得到四边形$E_{1}D_{1}FF_{1}$,它的周长记作$C_{2}$,…,照此规律作下去,则$C_{2023}$等于______.

答案： $\frac{1}{2^{2021}}$ 【解析】
∵ 点 D，E 分别为 AC，BC 边的中点，
∴ DE 是△ABC 的中位线，
∴ DE=$\frac{1}{2}$AB=$\frac{1}{2}$，AD=$\frac{1}{2}$AC=$\frac{1}{2}$，DE//AF，
∴ DE=AD.
∵ EF//AC，
∴ 四边形 EDAF 是平行四边形，
∴ AD=EF，DE=AF.又
∵ DE=AD，
∴ AD=EF=DE=AF，
∴ 四边形 EDAF 是菱形，
∴ C1=4×$\frac{1}{2}$=2.同理求得 C2=4×$\frac{1}{2^{2}}$=1，…，Cn=4×$\frac{1}{2^{n}}$=$\frac{1}{2^{n-2}}$(n 为正整数)，
∴ C2023=$\frac{1}{2^{2023-2}}$=$\frac{1}{2^{2021}}$.故答案为$\frac{1}{2^{2021}}$.

4 [2025 辽宁沈阳期中,中]如图,平面直角坐标系中,平行四边形 ABCD 的顶点 B 与原点 O 重合,顶点 C 落在 x 轴的正半轴上,在 AD 上截取$AF= AB$,分别以点 B,F 为圆心,大于$\frac {1}{2}BF$的长为半径画弧,两弧交于点 P,射线 AP 交 BC 于 E,若$AB= 5,BF= 6$,则点 F 的坐标为______.

答案： $(\frac{18}{5},\frac{24}{5})$ 【解析】连接 EF，设 AD 交 y 轴于点 H，AE，BF 交于点 G.
∵ 四边形 ABCD 为平行四边形，
∴ AD//BC，
∴ ∠FAE=∠BEA.由作图可知 AE 平分∠BAF，
∴ ∠BAE=∠FAE，
∴ ∠BAE=∠AEB，
∴ AB=BE=5.
∵ AF=AB，
∴ AF=BE.又
∵ AF//BE，
∴ 四边形 AFEB 为平行四边形.
∵ AB=BE，
∴ 四边形 AFEB 为菱形，
∴ AE⊥BF，BG=$\frac{1}{2}$BF=3，EG=$\sqrt{BE^{2}-BG^{2}}$=4，
∴ AE=2EG=8.
∵ S菱形AFEB=$\frac{1}{2}$AE·BF=AF·OH，
∴ OH=$\frac{24}{5}$.在 Rt△OFH 中，HF=$\sqrt{BF^{2}-OH^{2}}$=$\frac{18}{5}$，
∴ F$(\frac{18}{5},\frac{24}{5})$.故答案为$(\frac{18}{5},\frac{24}{5})$.

5 [2024 浙江杭州拱墅区调研,中]如图,在$□ ABCD$中,CE 平分$∠BCD$,交 AD 于点 E,DF 平分$∠ADC$,交 BC 于点 F,CE 与 DF 交于点 P,连接 EF,BP.
(1)求证:四边形 CDEF 是菱形;
(2)若$AB= 2,BC= 3,∠A= 120^{\circ }$,求 BP 的长.

答案：
（1）【证明】
∵ 四边形 ABCD 为平行四边形，
∴ AD//BC，
∴ ∠EDF=∠DFC.
∵ DF 平分∠ADC，
∴ ∠EDF=∠CDF，
∴ ∠DFC=∠CDF，
∴ CD=CF，同理可得 CD=DE，
∴ CF=DE.又
∵ CF//DE，
∴ 四边形 CDEF 是平行四边形.
∵ CD=CF，
∴ 四边形 CDEF 为菱形.
（2）【解】如图，过 P 作 PG⊥BC 于 G.
∵ AB=2，BC=3，∠A=120°，且四边形 CDEF 为菱形，
∴ CF=EF=CD=AB=2，∠ECF=$\frac{1}{2}$∠BCD=$\frac{1}{2}$∠A=60°，
∴ △CEF 为等边三角形，∠CPG=30°，
∴ CE=CF=2，
∴ PC=$\frac{1}{2}$CE=1，
∴ CG=$\frac{1}{2}$PC=$\frac{1}{2}$，
∴ BG=BC - CG=3−$\frac{1}{2}$=$\frac{5}{2}$，由勾股定理得，PG=$\frac{\sqrt{3}}{2}$.在 Rt△BPG 中，由勾股定理可得 BP=$\sqrt{BG^{2}+PG^{2}}=\sqrt{(\frac{5}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}=\sqrt{7}$，即 BP 的长为$\sqrt{7}$.

6 核心素养 几何直观 [2025 陕西西安质检,较难]如图所示,三角形纸片 ABC 中,$∠A= 37^{\circ }$,将其沿 DE 折叠后点 A 落在$A'$处,使$A'E// AB$,P 是 AB 上一动点,连接$BA',A'P$.当$BA'+A'P$取最小值时,$∠PA'B$的度数为______$^{\circ }$.

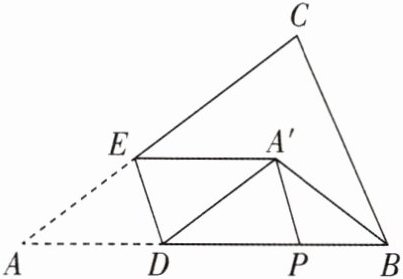
答案：
37 【解析】如图，连接 AA'.由折叠可得 AE=A'E，AD=A'D，∠AED=∠A'ED.
∵ A'E//AB，
∴ ∠A'ED=∠ADE，
∴ ∠AED=∠ADE，
∴ AE=AD，
∴ A'E=AE=AD=A'D，
∴ 四边形 ADA'E 是菱形，
∴ AA'平分∠BAC.作点 P 关于 AA'的对称点 P'，连接 A'P'，易知 P'在 AC 上，
∴ A'P=A'P'，
∴ BA'+A'P=A'P'+A'B，
∴ 当 B，A'，P'三点共线，且 BP'⊥AC 时，BA'+A'P 的值最小，此时∠APA'=∠AP'A'=90°，
∴ ∠BAC+∠PA'P'=180°.又
∵ ∠PA'B+∠PA'P'=180°，
∴ ∠BAC=∠PA'B=37°.故答案为 37.