第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
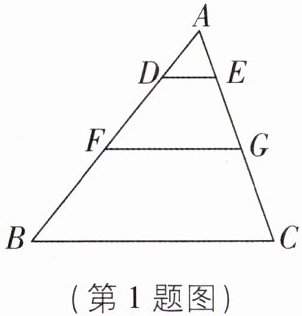
1 [2025 青海西宁校级质检,中]如图,$ \triangle A B C $ 中,$ D E // F G // B C $,$ A D : D F : F B = 2 : 3 : 4 $,若 $ E G = 4 $,则 $ A C $ 的长为( )
A.10
B.12
C.15
D.16

A.10
B.12
C.15
D.16
答案:
B [解析]
∵DE//FG//BC,
∴AE∶EG∶GC = AD∶DF∶FB = 2∶3∶4.
∵EG = 4,
∴$AE=\frac{8}{3}$,$GC=\frac{16}{3}$,
∴AC = AE + EG + GC = 12. 故选B.
∵DE//FG//BC,
∴AE∶EG∶GC = AD∶DF∶FB = 2∶3∶4.
∵EG = 4,
∴$AE=\frac{8}{3}$,$GC=\frac{16}{3}$,
∴AC = AE + EG + GC = 12. 故选B.
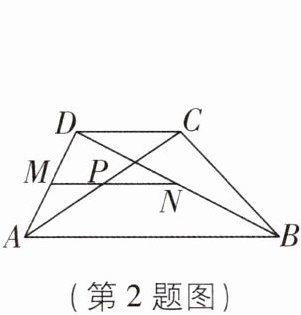
2 [中]如图,四边形 $ A B C D $ 中,$ A B // D C $,$ C D = 4 $,$ A B = 10 $,点 $ M $,$ N $ 分别是边 $ A D $ 和对角线 $ B D $ 的中点,且 $ M N $ 与对角线 $ A C $ 交于点 $ P $,则 $ P N $ 的长为( )
A.2
B.3
C.5
D.7

A.2
B.3
C.5
D.7
答案:
B [解析]
∵点M,N分别是边AD和对角线BD的中点,
∴MN是△ABD的中位线,
∴$MN=\frac{1}{2}AB = 5$,MN//AB.
∵AB//CD,
∴MN//CD,
∴$\frac{AM}{MD}=\frac{AP}{PC}$.
∵AM = DM,
∴AP = PC,
∴点P为AC的中点,
∴MP为△ACD的中位线,
∴$MP=\frac{1}{2}CD = 2$,
∴PN = MN - PM = 5 - 2 = 3,故选B.
∵点M,N分别是边AD和对角线BD的中点,
∴MN是△ABD的中位线,
∴$MN=\frac{1}{2}AB = 5$,MN//AB.
∵AB//CD,
∴MN//CD,
∴$\frac{AM}{MD}=\frac{AP}{PC}$.
∵AM = DM,
∴AP = PC,
∴点P为AC的中点,
∴MP为△ACD的中位线,
∴$MP=\frac{1}{2}CD = 2$,
∴PN = MN - PM = 5 - 2 = 3,故选B.
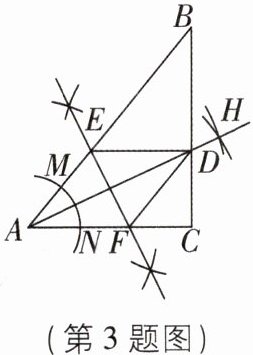
3 [中]如图,在 $ \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ B C = 9 $,以点 $ A $ 为圆心,适当长为半径画弧,分别交 $ A B $,$ A C $ 于点 $ M $,$ N $,分别以点 $ M $,$ N $ 为圆心,大于 $ \frac { 1 } { 2 } M N $ 的长为半径画弧,两弧交于点 $ H $,作射线 $ A H $ 交 $ B C $ 于点 $ D $,作线段 $ A D $ 的垂直平分线 $ E F $,分别交 $ A B $,$ A C $ 于点 $ E $,$ F $,连接 $ D E $,$ D F $,$ C D = 4 $,下列结论错误的是( )
A.$ A D $ 平分 $ \angle B A C $
B.$ A F = A E = D E = D F $
C.若 $ D F = 5 $,则 $ S _ { \triangle A D F } = 10 $
D.$ S _ { \triangle A D F } : S _ { \triangle C D F } = 5 : 4 $

A.$ A D $ 平分 $ \angle B A C $
B.$ A F = A E = D E = D F $
C.若 $ D F = 5 $,则 $ S _ { \triangle A D F } = 10 $
D.$ S _ { \triangle A D F } : S _ { \triangle C D F } = 5 : 4 $
答案:
C [解析]由作图可知,AD平分∠CAB,
∴∠CAD = ∠BAD.
∵EF垂直平分线段AD,
∴EA = ED,FA = FD,
∴∠EAD = ∠EDA,∠FAD = ∠FDA,
∴∠EDA = ∠DAF,∠EAD = ∠ADF,
∴DE//AF,AE//DF,
∴四边形AEDF是平行四边形.
∵EA = ED,
∴四边形AEDF是菱形,
∴AF = AE = DE = DF.
∵DF//AB,
∴CF∶AF = CD∶DB = 4∶5,
∴$S_{\triangle ADF}:S_{\triangle CDF}=5:4$,故选项A、B、D正确. 若DF = 5,则AF = 5,CF = 3,
∴CF∶AF = 3∶5,与已知条件矛盾,
∴DF不能为5,故选项C错误. 故选C.
∴∠CAD = ∠BAD.
∵EF垂直平分线段AD,
∴EA = ED,FA = FD,
∴∠EAD = ∠EDA,∠FAD = ∠FDA,
∴∠EDA = ∠DAF,∠EAD = ∠ADF,
∴DE//AF,AE//DF,
∴四边形AEDF是平行四边形.
∵EA = ED,
∴四边形AEDF是菱形,
∴AF = AE = DE = DF.
∵DF//AB,
∴CF∶AF = CD∶DB = 4∶5,
∴$S_{\triangle ADF}:S_{\triangle CDF}=5:4$,故选项A、B、D正确. 若DF = 5,则AF = 5,CF = 3,
∴CF∶AF = 3∶5,与已知条件矛盾,
∴DF不能为5,故选项C错误. 故选C.
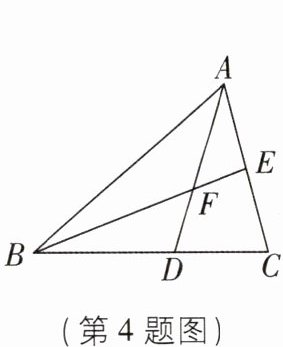
4 [中]如图,$ B E $ 是 $ \triangle A B C $ 的中线,点 $ F $ 在 $ B E $ 上,延长 $ A F $ 交 $ B C $ 于点 $ D $。若 $ B F = 3 F E $,$ B D = 3 $,则 $ D C = $____。

答案:
2添加辅助线
分析题目条件,出现了四条线段BF,FE,BD,DC,所以考虑平行线分线段成比例,想到作平行线,而只有BD的长是已知的,所以辅助线尽量不要破坏BD,这时考虑过F点作AC的平行线或过E点作AD的平行线,再联想到题目还给出BE为中线,所以E是AC的中点,所以过E点作AD的平行线.
【解析】如图,过点E作EP//AD交BC于点P.
∵BE是△ABC的中线,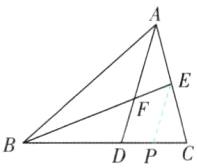
∴AE = CE,
∴DP = CP.
∵EP//DF,
∴$\frac{BD}{DP}=\frac{BF}{EF}=3$,
∴BD = 3DP = 3,
∴DP = 1,
∴DC = 2DP = 2.
2添加辅助线
分析题目条件,出现了四条线段BF,FE,BD,DC,所以考虑平行线分线段成比例,想到作平行线,而只有BD的长是已知的,所以辅助线尽量不要破坏BD,这时考虑过F点作AC的平行线或过E点作AD的平行线,再联想到题目还给出BE为中线,所以E是AC的中点,所以过E点作AD的平行线.
【解析】如图,过点E作EP//AD交BC于点P.
∵BE是△ABC的中线,

∴AE = CE,
∴DP = CP.
∵EP//DF,
∴$\frac{BD}{DP}=\frac{BF}{EF}=3$,
∴BD = 3DP = 3,
∴DP = 1,
∴DC = 2DP = 2.
5 [较难]如图,等腰三角形 $ A B C $ 中,$ A B = A C $,$ P $ 点在 $ B C $ 边上的高 $ A D $ 上,且 $ \frac { A P } { P D } = \frac { 1 } { 2 } $,$ B P $ 的延长线交 $ A C $ 于 $ E $,连接 $ D E $。若 $ S _ { \triangle A B C } = 10 $,则 $ S _ { \triangle A B E } = $____,$ S _ { \triangle D E C } = $____。
]
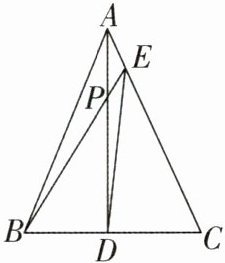
]

答案:
24 [解析]取EC中点F,连接DF.
∵AB = AC,AD为BC边上的高,
∴D为BC中点.
∵F为EC中点,
∴DF//BE,即DF//PE,
∴$\frac{AE}{EF}=\frac{AP}{PD}=\frac{1}{2}$,
∵$\frac{AE}{AC}=\frac{1}{5}$,
∴$\frac{S_{\triangle ABE}}{S_{\triangle ABC}}=\frac{AE}{AC}=\frac{1}{5}$,
∴$S_{\triangle ABE}=\frac{1}{5}S_{\triangle ABC}=\frac{1}{5}×10 = 2$,
∴$S_{\triangle BEC}=S_{\triangle ABC}-S_{\triangle ABE}=10 - 2 = 8$. 又
∵D为BC中点,
∴$S_{\triangle DEC}=\frac{1}{2}S_{\triangle BEC}=\frac{1}{2}×8 = 4$.
∵AB = AC,AD为BC边上的高,
∴D为BC中点.
∵F为EC中点,
∴DF//BE,即DF//PE,
∴$\frac{AE}{EF}=\frac{AP}{PD}=\frac{1}{2}$,
∵$\frac{AE}{AC}=\frac{1}{5}$,
∴$\frac{S_{\triangle ABE}}{S_{\triangle ABC}}=\frac{AE}{AC}=\frac{1}{5}$,
∴$S_{\triangle ABE}=\frac{1}{5}S_{\triangle ABC}=\frac{1}{5}×10 = 2$,
∴$S_{\triangle BEC}=S_{\triangle ABC}-S_{\triangle ABE}=10 - 2 = 8$. 又
∵D为BC中点,
∴$S_{\triangle DEC}=\frac{1}{2}S_{\triangle BEC}=\frac{1}{2}×8 = 4$.
6 核心素养 推理能力 [难]如图(1),$ l _ { 1 } // l _ { 2 } // l _ { 3 } $,直线 $ A B $,$ C H $ 与 $ l _ { 1 } $,$ l _ { 2 } $,$ l _ { 3 } $ 分别相交于点 $ A $,$ D $,$ B $ 和点 $ H $,$ E $,$ C $,$ A B $ 与 $ C H $ 交于点 $ O $,已知 $ C E = 6 $,$ H E = 3 $,$ A B = 12 $。
(1)尝试探究:在图(1)中,求出 $ D B $ 和 $ A D $ 的长。
(2)类比延伸:平移 $ A B $ 使得点 $ A $ 与点 $ H $ 重合,如图(2)所示,过点 $ D $ 作 $ D F // A C $,若 $ D E = 5 $,求线段 $ B F $ 的长。
(3)拓展迁移:如图(3),若某个三角形 $ A B C $ 的面积是 10,点 $ D $,$ E $ 分别位于 $ A B $,$ C A $ 上,$ D E // B C $,点 $ F $ 在 $ B C $ 上且 $ B F = 2 $,$ C F = 3 $,连接 $ A F $,$ E F $。如果 $ \triangle C B E $ 的面积和四边形 $ F C E D $ 的面积相等,求这个相等的面积值。
]
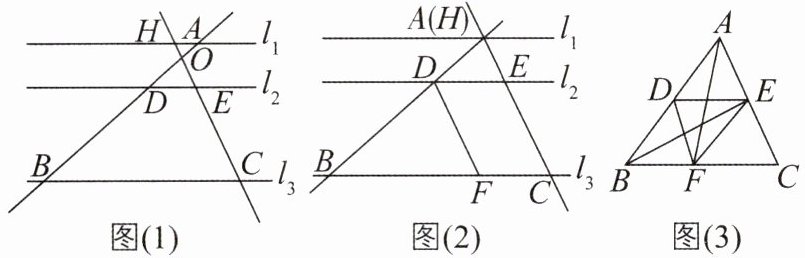
(1)尝试探究:在图(1)中,求出 $ D B $ 和 $ A D $ 的长。
(2)类比延伸:平移 $ A B $ 使得点 $ A $ 与点 $ H $ 重合,如图(2)所示,过点 $ D $ 作 $ D F // A C $,若 $ D E = 5 $,求线段 $ B F $ 的长。
(3)拓展迁移:如图(3),若某个三角形 $ A B C $ 的面积是 10,点 $ D $,$ E $ 分别位于 $ A B $,$ C A $ 上,$ D E // B C $,点 $ F $ 在 $ B C $ 上且 $ B F = 2 $,$ C F = 3 $,连接 $ A F $,$ E F $。如果 $ \triangle C B E $ 的面积和四边形 $ F C E D $ 的面积相等,求这个相等的面积值。
]

答案:
6.【解】
(1)如题图
(1),
∵$l_1// l_2// l_3$,CE = 6,HE = 3,AB = 12,
∴$\frac{AD}{AB}=\frac{HE}{HC}$,即$\frac{AD}{12}=\frac{3}{3 + 6}$,
∴AD = 4,
∴DB = AB - AD = 12 - 4 = 8.
(2)如题图
(2),由
(1)可知BD = 8,AD = 4.
∵DF//AC,DE//CF,
∴四边形DECF为平行四边形,
∴DE = CF = 5.
∵DF//AC,
∴$\frac{BF}{FC}=\frac{BD}{AD}$,即$\frac{BF}{5}=\frac{8}{4}$,
∴BF = 10.
(3)如题图
(3),
∵△CBE的面积和四边形FCED的面积相等,即$S_{\triangle BEF}+S_{\triangle CEF}=S_{\triangle CEF}+S_{\triangle DEF}$,
∴$S_{\triangle BEF}=S_{\triangle DEF}$,
∴EF//BD,
∴$\frac{CE}{AE}=\frac{CF}{FB}=\frac{3}{2}$
∴$S_{\triangle CBE}=\frac{3}{5}S_{\triangle ABC}=\frac{3}{5}×10 = 6$,即这个相等的面积值为6.
思路分析
如果把△ABE与△ABC看做同高的两个三角形,那么它们的面积之比等于底之比,即等于AE∶AC. 由于已知$S_{\triangle ABC}=10$,所以为了求出△ABE的面积,只需求出AE∶AC即可. 取EC中点F,连接DF. 先由等腰三角形“三线合一”的性质得出D为BC中点,再结合F为EC中点,根据三角形中位线定理证出DF//BE,再由平行线分线段成比例的基本事实求出AE∶EF,进而得出AE∶AC,即可得出$S_{\triangle ABE}$. 根据$S_{\triangle BEC}=S_{\triangle ABC}-S_{\triangle ABE}$,先求出$S_{\triangle BEC}$,再根据三角形的中线将三角形的面积二等分,得出$S_{\triangle DEC}$.
(1)如题图
(1),
∵$l_1// l_2// l_3$,CE = 6,HE = 3,AB = 12,
∴$\frac{AD}{AB}=\frac{HE}{HC}$,即$\frac{AD}{12}=\frac{3}{3 + 6}$,
∴AD = 4,
∴DB = AB - AD = 12 - 4 = 8.
(2)如题图
(2),由
(1)可知BD = 8,AD = 4.
∵DF//AC,DE//CF,
∴四边形DECF为平行四边形,
∴DE = CF = 5.
∵DF//AC,
∴$\frac{BF}{FC}=\frac{BD}{AD}$,即$\frac{BF}{5}=\frac{8}{4}$,
∴BF = 10.
(3)如题图
(3),
∵△CBE的面积和四边形FCED的面积相等,即$S_{\triangle BEF}+S_{\triangle CEF}=S_{\triangle CEF}+S_{\triangle DEF}$,
∴$S_{\triangle BEF}=S_{\triangle DEF}$,
∴EF//BD,
∴$\frac{CE}{AE}=\frac{CF}{FB}=\frac{3}{2}$
∴$S_{\triangle CBE}=\frac{3}{5}S_{\triangle ABC}=\frac{3}{5}×10 = 6$,即这个相等的面积值为6.
思路分析
如果把△ABE与△ABC看做同高的两个三角形,那么它们的面积之比等于底之比,即等于AE∶AC. 由于已知$S_{\triangle ABC}=10$,所以为了求出△ABE的面积,只需求出AE∶AC即可. 取EC中点F,连接DF. 先由等腰三角形“三线合一”的性质得出D为BC中点,再结合F为EC中点,根据三角形中位线定理证出DF//BE,再由平行线分线段成比例的基本事实求出AE∶EF,进而得出AE∶AC,即可得出$S_{\triangle ABE}$. 根据$S_{\triangle BEC}=S_{\triangle ABC}-S_{\triangle ABE}$,先求出$S_{\triangle BEC}$,再根据三角形的中线将三角形的面积二等分,得出$S_{\triangle DEC}$.
查看更多完整答案,请扫码查看


