《2025年初中必刷题九年级数学上册北师大版》

1 点P是$\triangle ABC$中AB边上一点(不与A,B重合),过P作直线截$\triangle ABC$,使截得的三角形与$\triangle ABC$相似,这样的直线最多作 ( )

A.2条
B.3条
C.4条
D.5条

答案：
C　[解析]
辅助线作法 图示 相似三角形
过 P 作 PE//AC △BPE∽△BAC
过 P 作 PE//BC △APE∽△ABC
过 P 作 ∠APE=∠C △APE∽△ACB
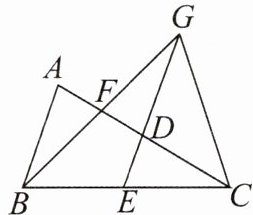
过 P 作 ∠BPE=∠C △BEP∽△BAC

2 如图,在$\triangle ABC$中,$AC= BC$,点D,E,F分别是线段AC,BC,AD的中点,BF,ED的延长线交于点G,连接GC.
(1)求证:$AB= GD$.
(2)当$CG= EG$时,求$\frac{AC}{AB}$的值.

答案：
(1)[证明]
∵D,E分别是线段AC,BC的中点，
∴DE为△ABC的中位线，
∴DE//AB，即EG//AB，
∴∠FDG=∠A.
∵点F为线段AD的中点，
∴AF=DF;在△ABF与△DGF中,{∠A=∠FDG, AF=DF, ∠AFB=∠DFG,
∴△ABF≌△DGF(ASA)，
∴AB=GD.
(2)[解]
∵DE为△ABC的中位线，
∴DE= $\frac{1}{2}$AB，CE= $\frac{1}{2}$BC= $\frac{1}{2}$AC.
∵DG=AB，EG=DE+DG，
∴EG= $\frac{3}{2}$AB.
∵DE//AB，
∴∠GEC=∠CBA.
∵AC=BC，CG=EG，
∴∠GCE=∠GEC=∠CBA=∠A，
∴△GEC∽△CBA，
∴ $\frac{CE}{AB}=\frac{CG}{AC}=\frac{EG}{BC}$，即 $\frac{\frac{1}{2}AC}{AB}=\frac{\frac{3}{2}AB}{AC}$，
∴ $\frac{AC}{AB}=\sqrt{3}$.

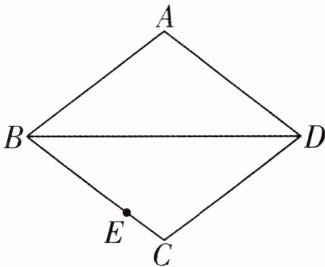
3 [2025福建福州质检]如图,已知菱形ABCD中,E是BC边上一点.
(1)在BC的右侧求作$\triangle AEF$,使得$EF// BD$,且$EF= \frac{1}{2}BD$(要求尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若$\angle EAF= \frac{1}{2}\angle ABC$,求证:$AE= \sqrt{2}EF$.

答案：

(1)[解]如图
(1)，△AEF即为所求(作法不唯一).
图
(1)
图
(2)
(2)[证明]如图
(2)，延长EF交AD的延长线于点M.
∵四边形ABCD是菱形，
∴AB=AD，BC//AD，BD平分∠ABC.
∵DB//EM，BE//DM，
∴四边形BEMD是平行四边形，
∴EM=BD.
∵BD=2EF，
∴EM=2EF.
∵AB=AD，
∴∠ABD=∠ADB= $\frac{1}{2}$∠ABC.
∵∠EAF= $\frac{1}{2}$∠ABC，
∴∠EAF=∠ADB.
∵BD//FM，
∴∠ADB=∠M，
∴∠EAF=∠M;
∵∠AEF=∠AEM，
∴△AEF∽△MEA，
∴ $\frac{AE}{ME}=\frac{EF}{AE}$，
∴AE²=EF·EM=2EF²，
∴AE= $\sqrt{2}$EF.

4 已知$\triangle ABC$中,$AB= 6$,$AC= 9$,D,E分别是直线AC和AB上的点,且$AD= 3$,要使$\triangle ADE\backsim\triangle ACB$,则$BE= $____.

答案： 4或8　[解析]
∵D,E分别是直线AC和AB上的点，
∴∠DAE=∠BAC，
∴若 $\frac{AD}{AC}=\frac{AE}{AB}$，根据两边成比例且夹角相等的两个三角形相似可以得到△ADE∽△ACB.
∵AB=6，AC=9，AD=3，
∴ $\frac{3}{9}=\frac{AE}{6}$，解得AE=2.分两种情况进行讨论:①D，E分别在线段AC和AB上时，
∵AE=2，AB=6，
∴BE=AB - AE=6 - 2=4;②D,E分别在线段AC和AB的反向延长线上时，
∵AE=2，AB=6，
∴BE=AB+AE=6+2=8.综上所述,BE的长为4或8.故答案为4或8.

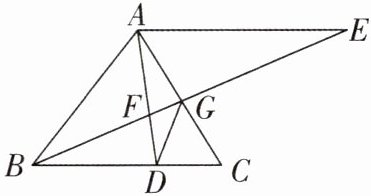
5 如图,在$\triangle ABC$中,点D在边BC上,$AE// BC$,BE与AD,AC分别相交于点F,G,$AF^{2}= FG\cdot FE$.
(1)求证:$\triangle CAD\backsim\triangle CBG$;
(2)连接DG,求证:$DG\cdot AE= AB\cdot AG$.

答案：
(1)[证明]
∵AF²=FG·FE，
∴ $\frac{AF}{FE}=\frac{FG}{AF}$.
∵∠AFG=∠EFA，
∴△AFG∽△EFA，
∴∠FAG=∠E，即∠DAC=∠E.
∵AE//BC，
∴∠CBG=∠E，
∴∠DAC=∠CBG.又
∵∠C=∠C，
∴△CAD∽△CBG.
(2)[证明]由
(1)知△CAD∽△CBG，
∴ $\frac{CA}{CB}=\frac{CD}{CG}$.
∵∠DCG=∠ACB，
∴△CDG∽△CAB，
∴ $\frac{DG}{AB}=\frac{CG}{CB}$.
∵AE//BC，
∴易证△AGE∽△CGB，
∴ $\frac{AE}{CB}=\frac{AG}{GC}$，
∴ $\frac{AG}{AE}=\frac{CG}{CB}$，
∴ $\frac{DG}{AB}=\frac{AG}{AE}$，
∴DG·AE=AB·AG.

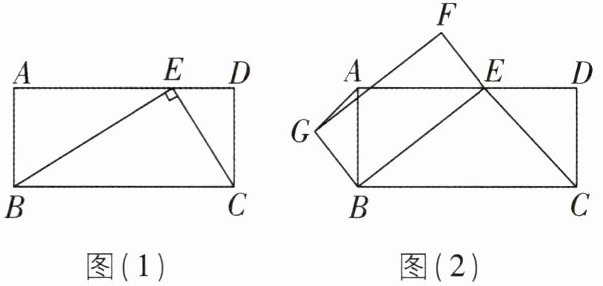
6 [2025山东济南质检]如图,在矩形ABCD中,$AB= 2$,$BC= 5$,点E是边AD上一点,连接BE,CE.
(1)如图(1),当$\angle BEC= 90^{\circ}$时,求AE的长度;
(2)如图(2),以BE为边在BE的左侧作矩形BEFG,且$BG:BE= 2:5$,连接AG.
①求证:$\angle BAG= \angle BCE$;
②求证:$AG\perp CE$.

答案：

(1)[解]
∵四边形ABCD是矩形，
∴AB=CD=2，BC=AD=5，∠A=∠D=90°.
∵∠BEC=90°，
∴∠AEB=90° - ∠DEC=∠DCE，
∴△ABE∽△DEC，
∴ $\frac{AB}{DE}=\frac{AE}{CD}$，
∴ $\frac{2}{5 - AE}=\frac{AE}{2}$，解得AE=4或1，经检验,AE=4和AE=1都是方程的解，且符合题意，
∴AE的长度是4或1.
(2)[证明]①
∵四边形ABCD是矩形，四边形BEFG是矩形，
∴∠ABC=∠GBE=90°，
∴∠ABC - ∠ABE=∠GBE - ∠ABE，即∠EBC=∠ABG.
∵AB=2，BC=5，BG:BE=2:5，
∴ $\frac{AB}{BC}=\frac{BG}{BE}$，
∴△ABG∽△CBE，
∴∠BAG=∠BCE.②延长CE,GA交于M，如图.
∵四边形ABCD是矩形，
∴∠BAD=90°，AD//BC，
∴∠BAG+∠MAE=90°，∠MEA=∠BCE.由①知∠BAG=∠BCE，
∴∠BAG=∠MEA，
∴∠MEA+∠MAE=90°，
∴∠M=90°，
∴AG⊥CE.

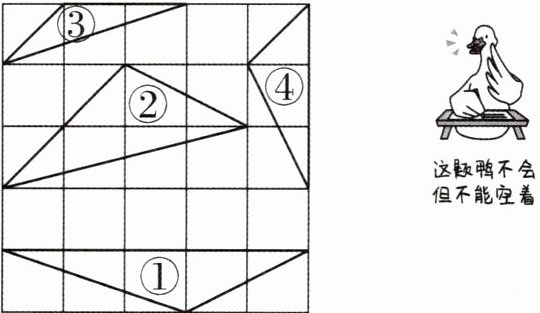
7 如图,四个三角形的顶点都在方格的格点上,其中相似的两个三角形是 ( )

A.①④
B.①③
C.②③
D.②④

答案： B　[解析]设小方格的边长为1.三角形①的边长分别为 $\sqrt{10}$, $\sqrt{5}$,5；三角形②的边长分别为 $\sqrt{5}$, $2\sqrt{2}$, $\sqrt{17}$；三角形③的边长分别为2, $\sqrt{2}$, $\sqrt{10}$；三角形④的边长分别为3, $\sqrt{2}$, $\sqrt{5}$，对应边成比例的是①和③.故选B.