《2025年初中必刷题九年级数学上册北师大版》

1 [2025河南平顶山期中]若四条线段a,b,c,d成比例,其中b= 2cm,c= 2cm,d= 4cm,则线段a的长为( )

A.1cm
B.2cm
C.3cm
D.12cm

答案： A【解析】根据题意可得$\frac{a}{b}=\frac{c}{d}$，
∵$\frac{a}{2}=\frac{2}{4}$，
∴a=1cm.故选A.

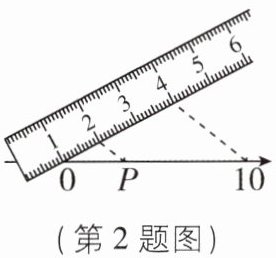
2 [2025广东汕头质检]如图是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点P表示的数是( )

A.√2
B.2
C.10/3
D.5

答案： C【解析】设P点表示的数为x，则根据平行线分线段成比例可得$\frac{x}{10 - x}=\frac{1}{4 - 2}$，解得x=$\frac{10}{3}$，经检验，x=$\frac{10}{3}$是分式方程的解，即P点表示的数为$\frac{10}{3}$.故选C.

3 如图,一座正方形城池北边、西边正中A,C处各开一道门,从点A往正北方向走40步刚好有一棵树位于点B处,从点C往正西方向走810步到达点D处时正好看到此树,则正方形城池的边长为( )

A.360步
B.270步
C.180步
D.90步

答案： A【解析】设正方形城池的边长为x步，则AE=CE=$\frac{1}{2}$x.
∵AE//CD，
∴∠BEA=∠EDC，
∴Rt△BEA∽Rt△EDC，
∴$\frac{AB}{EC}=\frac{AE}{CD}$，即$\frac{40}{\frac{1}{2}x}=\frac{\frac{1}{2}x}{810}$，
∴x=360(负值已舍去)，即正方形城池的边长为360步.故选A.

4 [2023江苏徐州中考]如图,在△ABC中,∠B= 90°,∠A= 30°,BC= 2,D为AB的中点.若点E在边AC上,且AD/AB= DE/BC,则AE的长为( )

A.1
B.2
C.1或√3/2
D.1或2

答案：
D【解析】在△ABC中，∠B=90°，∠A=30°，BC=2，
∴AC=2BC=4，∠C=60°，
∴由勾股定理得AB=2$\sqrt{3}$.
∵点D是AB的中点，
∴AD=$\sqrt{3}$.如图
(1)，当∠ADE=90°时，
∵∠ADE=∠ABC，$\frac{AD}{AB}=\frac{DE}{BC}$，
∴△ADE∽△ABC，
∴$\frac{AE}{AC}=\frac{AD}{AB}=\frac{1}{2}$，
∴AE=2.

如图
(2)，当∠ADE'≠90°时，取AC的中点H，连接DH.
∵点D是AB中点，点H是AC的中点，
∴DH//BC，DH=$\frac{1}{2}$BC=1，
∴∠AHD=∠C=60°，DH=DE'=1，
∴∠DE'H=60°，
∴∠ADE'=∠A=30°，
∴AE'=DE'=1.故选D.

5 [2025湖北武汉调研]顶角为36°的等腰三角形称为黄金三角形,如图所示,△ABC中,AB= AC,∠A= 36°,其中BC/AC= (√5 - 1)/2≈0.618.作∠ABC的平分线$BC_1,$交AC于$C_1,$得到黄金三角形$BCC_1；$作$C_1B_1//BC$交AB于$B_1,B_1C_2//BC_1$交AC于$C_2,$得到黄金三角形$B_1C_1C_2；$作$C_2B_2//BC$交AB于$B_2,B_2C_3//BC_1$交AC于$C_3,$得到黄金三角形$B_2C_2C_3；$…,依次类推,我们可以得到无数个黄金三角形.若BC的长为1,那么$C_5C_6$的长为( )

A.√5 - 2
B.9 - 4√5
C.2√5 - 4
D.(13√5 - 29)/2

答案： B【解析】
∵△ABC中，AB=AC，∠A=36°，
∴∠ABC=∠ACB=72°.
∵BC₁平分∠ABC，
∴∠C₁BC=∠ABC₁=36°，
∴AC₁=BC₁，△ABC∽△BCC₁，∠CC₁B=72°=∠ACB，
∴$\frac{AB}{BC}=\frac{BC}{CC₁}$，BC=BC₁，
∴AC₁=BC₁=BC=1.设CC₁=x，则AB=AC=1+x，
∴$\frac{1 + x}{1}=\frac{1}{x}$，
∴x=$\frac{-1\pm\sqrt{5}}{2}$.
∵x＞0，
∴CC₁=x=$\frac{\sqrt{5}-1}{2}$.
∵B₁C₂//BC₁，
∴∠C₂B₁C₁=∠B₁C₁B.又
∵C₁B₁//BC，
∴∠B₁C₁B=∠C₁BC，∠B₁C₁C₂=∠BCC₁，
∴∠C₂B₁C₁=∠C₁BC，
∴△BCC₁∽△B₁C₁C₂，△ABC∽△AB₁C₁，
∴$\frac{C₁C₂}{CC₁}=\frac{B₁C₁}{BC}$，$\frac{B₁C₁}{BC}=\frac{AC₁}{AC}$.
∵AC₁=BC₁=BC=1，
∴$\frac{C₁C₂}{CC₁}=\frac{AC₁}{AC}=\frac{\sqrt{5}-1}{2}$，
∴C₁C₂=$(\frac{\sqrt{5}-1}{2})^2=\frac{3-\sqrt{5}}{2}$，同理得C₂C₃=$(\frac{\sqrt{5}-1}{2})^3=\sqrt{5}-2$，……，
∴C₅C₆=$(\frac{\sqrt{5}-1}{2})^6=(\sqrt{5}-2)^2=9 - 4\sqrt{5}$.故选B.

6 [2025山东临沂质检]如图,将一张腰长为12cm的等腰三角形纸片,沿与底边平行的方向剪去一张小的等腰三角形纸片,剩下一张等腰梯形纸片.若剪去的纸片面积是剩下的纸片面积的1/8,则剪去的等腰三角形纸片的腰长为______.

答案： 4cm【解析】由题可知，剪去的三角形纸片面积是原三角形纸片面积的$\frac{1}{9}$，且剪去的三角形与原三角形相似，
∴两个三角形的相似比为$\frac{1}{3}$，
∴剪去的等腰三角形纸片的腰长为$\frac{1}{3}×12 = 4$(cm).故答案为4cm.

7 如图,矩形ABCD的边AB= 3cm,对角线AC= 3√5cm,动点M从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时动点N从点D出发,沿DA以2cm/s的速度向点A匀速运动.设运动的时间为t s,当t= ______时,△ACD与△AMN相似.

答案：
1.5或2.4【解析】由题意，得AD=BC=$\sqrt{(3\sqrt{5})^2-3^2}$=6(cm)，DN=2t cm，AM=t cm，则AN=(6 - 2t)cm.当△ACD∽△NMA时，$\frac{AD}{AN}=\frac{CD}{AM}$，即$\frac{6}{6 - 2t}=\frac{3}{t}$，解得t=1.5.当△ACD∽△MNA时，$\frac{AD}{AM}=\frac{CD}{AN}$，即$\frac{6}{t}=\frac{3}{6 - 2t}$，解得t=2.4.所以当t=1.5或2.4时，△ACD与△AMN相似.

8 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,若BF：FD= 3：1,AB+BE= 3√3,则△ABC的周长为______.

答案：
5$\sqrt{3}$【解析】如图，过点F作FM⊥AB于点M，FN⊥AC于点N，过点D作DT//AE交BC于点T.
∵AE平分∠BAC，FM⊥AB，FN⊥AC，
∴FM=FN，
∴$\frac{S_{\triangle ABF}}{S_{\triangle ADF}}=\frac{BF}{DF}=\frac{\frac{1}{2}\cdot AB\cdot FM}{\frac{1}{2}\cdot AD\cdot FN}=3$，
∴AB=3AD.设AD=DC=a，则AB=3a.
∵AD=DC，DT//AE，
∴ET=CT，$\frac{BE}{ET}=\frac{BF}{DF}=3$.设ET=CT=b，则BE=3b.
∵AB+BE=3$\sqrt{3}$，
∴3a+3b=3$\sqrt{3}$，
∴a + b=$\sqrt{3}$，
∴△ABC的周长为AB+AC+BC=5a+5b=5$\sqrt{3}$，故答案为5$\sqrt{3}$.