《2025年初中必刷题九年级数学上册北师大版》

1[2025辽宁抚顺质检,中]下列描述小明和小颖在同一盏路灯下影子情况的图片中合理的是( )

答案： 1.D 【解析】小明和小颖在同一盏路灯下的影子方向相反，且他们影子的顶端分别与他们各自的头顶以及路灯顶端在同一条直线上。故选D。

2[2025陕西榆林校级期末,中]小阳和小明两人从远处沿直线走到路灯下,他们规定小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离( )

A.始终不变
B.越来越远
C.时近时远
D.越来越近

答案： 2.D 【解析】因为小阳和小明两人从远处沿直线走到路灯下这一过程中离光源越来越近，所以小阳在地上的影子越来越短，所以他们两人之间的距离越来越近。故选D。

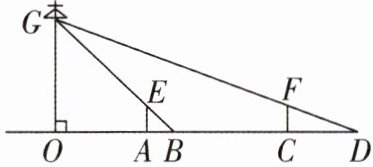
3[2024广西贵港期中,中]如图,一路灯OG高5.6米,身高1.6米的小方从距离路灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增加3米,小方行走的路程是____米.
]

答案： 3.7.5 【解析】
∵AE⊥OD，GO⊥OD，
∴EA//GO，
∴△AEB∽△OGB，
∴$\frac{AE}{GO}=\frac{AB}{BO}$，
∴$\frac{1.6}{5.6}=\frac{AB}{AB + 5}$，解得AB = 2。
∵沿OA所在的直线行走到点C时，人影长度增加3米，
∴DC = 5，同理可得△DFC∽△DGO，
∴$\frac{FC}{GO}=\frac{CD}{DO}$，即$\frac{1.6}{5.6}=\frac{5}{5 + 5 + AC}$，解得AC = 7.5。故答案为7.5。

4[2024山东东营调研,中]如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影子为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F.
(1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影子FH(不写画法);
(2)求小明(EF)到达点F时的影子FH的长.
]

答案：
4.【解】
(1)如图，点O和FH为所作。

(2)由题意得，BM = BD = 3，GD = 1.2，DF = 1.5×1.5×2 = 4.5。设AB = CD = EF = a，作OK⊥MN于K，如上图。
∵AB//OK，
∴△MAB∽△MOK，
∴$\frac{AB}{OK}=\frac{MB}{MK}$，即$\frac{a}{OK}=\frac{3}{6 + DK}$①；
∵CD//OK，
∴△GCD∽△GOK，
∴$\frac{CD}{OK}=\frac{GD}{GK}$，即$\frac{a}{OK}=\frac{1.2}{1.2 + DK}$②。由①②得$\frac{3}{6 + DK}=\frac{1.2}{1.2 + DK}$，解得DK = 2，
∴$\frac{a}{OK}=\frac{3}{6 + 2}=\frac{3}{8}$，FK = DF - DK = 4.5 - 2 = 2.5。
∵EF//OK，
∴△HEF∽△HOK，$\frac{EF}{OK}=\frac{HF}{HK}$，即$\frac{HF}{HF + 2.5}=\frac{3}{8}$，
∴HF = 1.5。
答：小明到达点F时的影子FH的长为1.5米。

5核心素养运算能力[较难]如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的右端点运动到M点的时刻为0,用t(秒)表示l的运动时间.
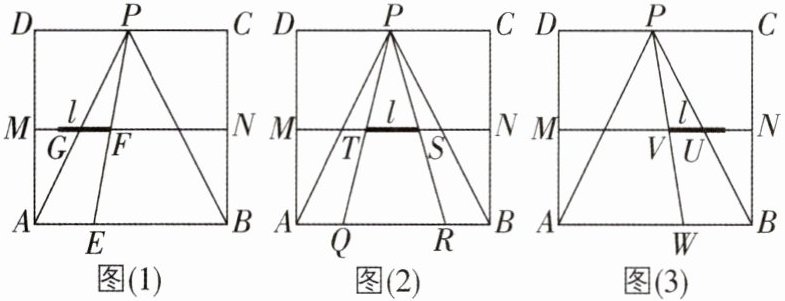
(1)请你针对图(1)、图(2)、图(3)中l位于不同位置的情形,分别画出在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2.②2≤t≤3.③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
]

答案：
5.【解】
(1)如图：



(2)①当t = 1时，不会形成盲区，则y = 0。当1＜t≤2时，△PAB内的盲区是梯形AEFG。MG，FG分别是△PAD，△PAE的中位线，
∴$MG=\frac{1}{2}PD = 1$，FG = t - 1，AE = 2(t - 1)。而梯形AEFG的高为2，
∴$y=\frac{1}{2}[(t - 1)+2(t - 1)]×2 = 3t - 3$。
∴当1≤t≤2时，y = 3t - 3。
②当2≤t≤3时，△PAB内的盲区是梯形QRST。易知TS = 1，QR = 2，而梯形QRST的高为2，
∴$y=\frac{1}{2}(1 + 2)×2 = 3$。
③当3≤t＜4时，△PAB内的盲区是梯形WBUV。易知UV = 1 - (t - 3) = 4 - t，WB = 2(4 - t)，而梯形WBUV的高为2，
∴$y=\frac{1}{2}[(4 - t)+2(4 - t)]×2 = 12 - 3t$。
当t = 4时，不会形成盲区，则y = 0。
∴当3≤t≤4时，y = 12 - 3t。
当1≤t≤2时，盲区的面积y由0逐渐增大到3；当2≤t≤3时，盲区的面积y为定值3；当3≤t≤4时，盲区的面积y由3逐渐减小到0。
关键点拨
本题考查的是相似三角形在中心投影中的实际应用，找出相似三角形，再利用相似三角形对应边成比例求解。
刷有所得
太阳的位置和高度决定了影子的方向和长短。一天中，阳光下物体的影子变化规律是上午影子由长逐渐变短；下午影子由短逐渐变长。方向由西逐渐转向东。
刷有所得
视点、视角和盲区：把观察者所处的位置定为一点，叫视点；人眼到视平面的距离是固定的(视距)，视平面左右两个边缘到人眼的连线得到的角就是视角；视线到达不了的区域为盲区。