《2025年初中必刷题九年级数学上册北师大版》

8 新考法 [2025 广西玉林期末,中]如图(1),在边长为 4 的正方形 ABCD 中,点 H 为 AB 上一动点,且 $2 \leq BH ＜ 4$,截取 $HM = HB$,且 HM 交线段 AD 于 M,过 M 作 HM 的垂线 MN 交 DC 于 N。
(1)求证：$\triangle AHM \backsim \triangle DMN$；
(2)如图(2),若点 M 是 AD 的中点,求 $\triangle DMN$ 的周长；
(3)在动点 H 逐渐向点 A 运动(HB 逐渐增大)的过程中,$\triangle DMN$ 的周长如何变化？请说明理由。
]

答案：
(1)【证明】$\because$ 四边形ABCD是正方形，$\therefore \angle D = \angle A = 90^{\circ}$。$\because HM\perp MN$，$\therefore \angle HMN = 90^{\circ}$，$\therefore \angle DMN+\angle AMH=\angle AHM+\angle AMH = 90^{\circ}$，$\therefore \angle AHM=\angle DMN$，$\therefore \triangle AHM\backsim \triangle DMN$。
(2)【解】$\because$ 点M是AD的中点，正方形ABCD的边长为4，$\therefore MD = AM = 2$。设$HM = HB = x$，则$AH = 4 - x$。在$Rt\triangle AHM$中，$AH^{2}+AM^{2}=HM^{2}$，$\therefore (4 - x)^{2}+2^{2}=x^{2}$，解得$x = 2.5$，$\therefore AH = 1.5$。$\because \triangle AHM\backsim \triangle DMN$，$\therefore \frac{AM}{DN}=\frac{MH}{MN}=\frac{AH}{MD}$，即$\frac{2}{DN}=\frac{2.5}{MN}=\frac{1.5}{2}$，$\therefore DN=\frac{8}{3}$，$MN=\frac{10}{3}$，$\therefore \triangle DMN$的周长为$DN + MN + DM=\frac{8}{3}+\frac{10}{3}+2 = 8$。
(3)$\triangle DMN$的周长是一个定值，始终为8，理由如下：设$HM = HB = x$，则$AH = 4 - x$。在$Rt\triangle AHM$中，$AH^{2}+AM^{2}=HM^{2}$，$\therefore (4 - x)^{2}+AM^{2}=x^{2}$，即$AM = \sqrt{8x - 16}$，$\therefore DM = 4 - AM = 4 - \sqrt{8x - 16}$。$\because \triangle AHM\backsim \triangle DMN$，且相似比为$\frac{AH}{MD}=\frac{4 - x}{4 - \sqrt{8x - 16}}$，$\therefore C_{\triangle DMN}=C_{\triangle AHM}\cdot \frac{4 - \sqrt{8x - 16}}{4 - x}=(4 - x + x + \sqrt{8x - 16})\cdot \frac{4 - \sqrt{8x - 16}}{4 - x}=8$。$\therefore$ 在动点H逐渐向点A运动的过程中，$\triangle DMN$的周长是一个定值，始终为8。

9 核心素养 模型观念 [较难]如图(1)所示,在 $\triangle ABC$ 中,$AB = 4$,D 是 AB 上一点(不与 A,B 重合),DE // BC 交 AC 于点 E,连接 CD。设 $\triangle ABC$ 的面积为 S,$\triangle DEC$ 的面积为 $S'$。
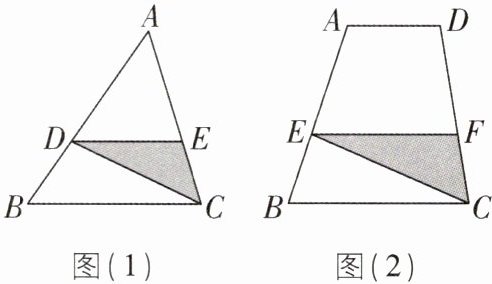
(1)当 $AD = 3$ 时,$\triangle ADE$ 的面积是 6,求 $S'$ 的值；
(2)当 $AD = 3$ 时,求 S 的值(结果用含字母 $S'$ 的代数式表示)；
(3)如图(2)所示,在四边形 ABCD 中,$AB = 4$,$AD // BC$,$AD = \frac{1}{2}BC$,E 是 AB 上一点(不与 A,B 重合),EF // BC 交 CD 于点 F,连接 CE。设 $AE = n$,四边形 ABCD 的面积为 S,$\triangle CEF$ 的面积为 $S'$,请你利用前面问题的解法或结论,用含字母 n 的代数式表示 $\frac{S'}{S}$。
]

答案： 【解】
(1)$\because AB = 4$，$AD = 3$，$\therefore BD = 1$。$\because DE// BC$，$\therefore CE:AE = BD:AD = 1:3$，$\therefore S':S_{\triangle ADE}=CE:AE = 1:3$。$\because \triangle ADE$的面积是6，$\therefore S'=\frac{1}{3}× 6 = 2$。
(2)$\because DE// BC$，$\therefore$ 易得$\triangle ADE\backsim \triangle ABC$。又$\because AD:AB = 3:4$，$\therefore \frac{S_{\triangle ADE}}{S}=(\frac{3}{4})^{2}=\frac{9}{16}$，$\therefore S=\frac{16}{9}S_{\triangle ADE}$。由
(1)知$S'=\frac{1}{3}S_{\triangle ADE}$，$\therefore S=\frac{16}{3}S'$。
(3)延长BA，CD交于点O，如图。$\because AD// BC$，$\therefore$ 易得$\triangle OAD\backsim \triangle OBC$，$\therefore \frac{OD}{OC}=\frac{OA}{OB}=\frac{AD}{BC}=\frac{1}{2}$，$\therefore OA = AB = 4$，$OB = 8$。$\because AE = n$，$\therefore OE = 4 + n$，$BE = 4 - n$。
$\because EF// BC$，$\therefore \frac{CF}{OF}=\frac{BE}{OE}=\frac{4 - n}{4 + n}$，且易得$\triangle OEF\backsim \triangle OBC$，$\therefore \frac{S_{\triangle OEF}}{S_{\triangle OBC}}=(\frac{OE}{OB})^{2}$，$\therefore \frac{S_{\triangle CEF}}{S_{\triangle OBC}}=\frac{S_{\triangle CEF}}{S_{\triangle OEF}}\cdot \frac{S_{\triangle OEF}}{S_{\triangle OBC}}=\frac{4 - n}{4 + n}\cdot (\frac{4 + n}{8})^{2}=\frac{16 - n^{2}}{64}$。$\because \frac{S_{\triangle OAD}}{S_{\triangle OBC}}=(\frac{OA}{OB})^{2}=\frac{1}{4}$，$\therefore \frac{S_{四边形ABCD}}{S_{\triangle OBC}}=\frac{3}{4}$，$\therefore \frac{S'}{S}=\frac{S_{\triangle CEF}}{\frac{3}{4}S_{\triangle OBC}}=\frac{4}{3}× \frac{16 - n^{2}}{64}=\frac{16 - n^{2}}{48}$。

1 直角三角形内接四边形 [2025 上海静安区校级期中,中]如图,在 $Rt\triangle ABC$ 中,$\angle C = 90^\circ$,$BC = 6$,$AC = 8$,四边形 DEGF 为内接正方形,那么 $AD:EB = $ ____。

答案： $16:9$

2 任意三角形内接四边形 [2025 山东菏泽质检,中]如图,在 $\triangle ABC$ 中,$AD \perp BC$,垂足为 D,$AD = 5$,$BC = 10$,四边形 EFGH 和四边形 HGNM 均为正方形,且点 E,F,G,N,M 都在 $\triangle ABC$ 的边上,EH 与 AD 交于点 P,那么 $\triangle AEM$ 与四边形 BCME 的面积比为 ____。

答案： $1:3$