《2025年初中必刷题九年级数学上册北师大版》

1[中]探讨关于x的一元二次方程$a x ^ { 2 } + b x - 1 = 0$总有实数根的条件,三名同学给出结论:甲:a,b同号;乙:$a - b - 1 = 0$;丙:$a + b - 1 = 0$.下列说法正确的是( )

A.甲、乙、丙都正确
B.只有甲不正确
C.甲、乙、丙都不正确
D.只有乙正确

答案： B【解析】
∵ax²+bx-1=0，
∴Δ=b²+4a.若a，b同号，令a=-1,b=-1，此时Δ=1-4=-3＜0，方程没有实数解，
∴甲错误；若a-b-1=0，即a=b+1，
∴Δ=b²+4(b+1)=(b+2)²≥0，方程总有实数根，
∴乙正确；若a+b-1=0，即a=-b+1，
∴Δ=b²+4(-b+1)=(b-2)²≥0，方程总有实数根，
∴丙正确，故选B.

2[2024河北石家庄期中,中]小刚在解关于x的方程$2 a x ^ { 2 } - b x + 2 = 0 ( a \neq 0 )$时,将其抄成了$2 a x ^ { 2 } + b x + 2 = 0$,得到一个解是$x = - 2$,则原方程的根的情况是( )

A.不存在实数根
B.有两个实数根
C.有一个根是$x = - 2$
D.不确定

答案：
B
思路引导 一元二次方程中看错问题

错解→代入(将错就错)→看错的方程→b=4a+1→代入→原方程→判别式→2ax²-(4a+1)x+2=0→判断→根的情况
【解析】把x=-2代入2ax²+bx+2=0得8a-2b+2=0，
∴b=4a+1.把b=4a+1代入方程2ax²-bx+2=0得2ax²-(4a+1)x+2=0.
∵(4a+1)²-4×2a×2=(4a-1)²≥0，
∴方程2ax²-bx+2=0(a≠0)有两个实数根.故选B.

3[2024河南驻马店期中,中]如图,点A在数轴的负半轴,点B在数轴的正半轴,且点A对应的数是$2 x - 1$,点B对应的数是$x ^ { 2 } + x$,已知$A B = 5$,则x的值为____.

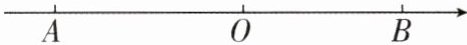
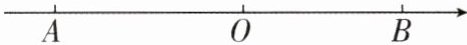
答案： $\frac{1 - \sqrt{17}}{2}$【解析】根据题意，得x²+x-(2x-1)=5，整理，得x²-x-4=0.
∵a=1,b=-1,c=-4，
∴Δ=(-1)²-4×1×(-4)=17＞0，则x=$\frac{-b±\sqrt{b²-4ac}}{2a}$=$\frac{1±\sqrt{17}}{2}$，
∴x₁=$\frac{1+\sqrt{17}}{2}$，x₂=$\frac{1 - \sqrt{17}}{2}$.
∵点A在数轴的负半轴，
∴2x-1＜0，即x＜$\frac{1}{2}$，
∴x=$\frac{1 - \sqrt{17}}{2}$，故答案为$\frac{1 - \sqrt{17}}{2}$.

4[2024重庆江北区期末,中]已知实数m,n满足$m ^ { 2 } - m n + n ^ { 2 } = 3$,设$P = m ^ { 2 } + m n - n ^ { 2 }$,则P的最大值为____.

答案： 5【解析】
∵m²-mn+n²=3，P=m²+mn-n²，
∴将两个等式相加得P+3=2m²，则P=2m²-3，要求P的最大值，只需求出m²的最大值.将m²-mn+n²=3看成关于n的一元二次方程，整理得n²-mn+m²-3=0.
∵方程有实数解，
∴Δ=m²-4(m²-3)≥0，
∴m²≤4，即m²的最大值为4，
∴当m²=4时，P的最大值为5.故答案为5.

5[2025内蒙古呼和浩特调研,中]已知关于x的一元二次方程$a x ^ { 2 } - 2 ( a - 1 ) x + a - 2 = 0 ( a ＞ 0 )$,设方程的两个实数根分别为$x _ { 1 } , x _ { 2 }$(其中$x _ { 1 } ＞ x _ { 2 }$),若y是关于a的函数,且$y = x _ { 1 } - a x _ { 2 }$,当$y ＞ 0$时,a的取值范围为____.

答案： 0 ＜ a ＜ 3【解析】
∵ax²-2(a - 1)x + a - 2 = 0(a ＞ 0)是关于x的一元二次方程，
∴Δ=[-2(a - 1)]²-4a(a - 2)=4＞0，
∴x=$\frac{2(a - 1)±2}{2a}$，
∴x = 1或x = 1 - $\frac{2}{a}$.
∵a ＞ 0，x₁＞x₂，
∴x₁ = 1，x₂ = 1 - $\frac{2}{a}$，
∴y = x₁ - ax₂ = 1 - a，(1 - $\frac{2}{a}$)=1 - a + 2 = 3 - a＞0，解得a ＜ 3，
∴0 ＜ a ＜ 3，故答案为0 ＜ a ＜ 3.

6[2025河南洛阳校级质检,中]已知关于x的方程$( 2 - k ) x ^ { 2 } + k x - 2 = 0$.
(1)求证:无论k取何值,此方程总有实数根;
(2)若此方程有两个整数根,求正整数k的值.

答案：
(1)【证明】当2 - k = 0，即k = 2时，方程为2x - 2 = 0，解得x = 1；当2 - k≠0，即k≠2时，方程为一元二次方程，Δ=k²-4(2 - k)×(-2)=k²-8k + 16=(k - 4)²≥0，则此时方程有实数根.
∴无论k取何值，此方程总有实数根.
(2)【解】
∵此方程有两个整数根，
∴k≠2，解得x₁=$\frac{-k-(k - 4)}{2(2 - k)}$=1，x₂=$\frac{-k+(k - 4)}{2(2 - k)}$=$\frac{-2}{2 - k}$=$\frac{2}{k - 2}$.
∵x₁,x₂为整数，k为正整数，
∴k = 1或k = 3或k = 4.

7[中]已知关于x的一元二次方程$x ^ { 2 } - ( 2 m + 3 ) x + m ^ { 2 } + 3 m + 2 = 0$.
(1)若$x = 2$是方程的一个根,求m的值;
(2)以这个方程的两个实数根作为$\triangle A B C中A B , A C ( A B ＜ A C )$的长,当$B C = \sqrt { 5 }$时,$\triangle A B C$是直角三角形,求此时m的值.

答案： 【解】
(1)
∵x = 2是方程的一个根，
∴4 - 2(2m + 3)+m²+3m + 2 = 0，整理得m²-m = 0，
∴m = 0或m = 1.
(2)
∵Δ=[-(2m + 3)]²-4(m²+3m + 2)=1，
∴x=$\frac{2m + 3±1}{2}$，
∴x₁ = m + 2，x₂ = m + 1.
∵AB,AC(AB ＜ AC)的长是这个方程的两个实数根，
∴AC = m + 2＞0，AB = m + 1＞0，
∴m ＞ -1.
∵BC = $\sqrt{5}$，△ABC是直角三角形，
∴当BC为斜边时，有(m + 2)²+(m + 1)²=($\sqrt{5}$)²，解得m₁=-3(不符合题意，舍去)，m₂ = 0；当AC为斜边时，有($\sqrt{5}$)²+(m + 1)²=(m + 2)²，解得m = 1.综上所述，m的值为0或1.

8核心素养运算能力[2024江西南昌期中,较难]对于任意一个三位数k,如果k满足各个数位上的数字都不为零,且十位上的数字的平方等于百位上的数字与个位上的数字之积的4倍,那么称这个数为“喜鹊数”.例如:$k = 169$,因为$6 ^ { 2 } = 4 × 1 × 9$,所以169是“喜鹊数”.
(1)已知一个“喜鹊数”$k = 100 a + 10 b + c ( 1 \leq a \leq 9 , 1 \leq b \leq 9 , 1 \leq c \leq 9$,且a,b,c为整数),请直接写出a,b,c所满足的关系式:____;241____“喜鹊数”(填“是”或“不是”).
(2)利用(1)中“喜鹊数”k中的a,b,c构造两个一元二次方程①$a x ^ { 2 } + b x + c = 0$与②$c x ^ { 2 } + b x + a = 0$,若$x = m$是方程①的一个根,$x = n$是方程②的一个根,求m与n满足的关系式.
(3)在(2)的条件下,若$m + n = - 2$,请直接写出满足条件的所有k的值.

答案： 【解】
(1)
∵k = 100a + 10b + c是“喜鹊数”(1≤a≤9,1≤b≤9,1≤c≤9，且a,b,c为整数)，
∴b²=4ac，即b²-4ac = 0.
∵4²=16，4×2×1 = 8，16≠8，
∴241不是“喜鹊数”.故答案为b²-4ac = 0，不是.
(2)
∵x = m是一元二次方程ax²+bx + c = 0的一个根，x = n是一元二次方程cx²+bx + a = 0的一个根，
∴am²+bm + c = 0，cn²+bn + a = 0.将cn²+bn + a = 0两边同除以n²得a($\frac{1}{n}$)²+b($\frac{1}{n}$)+c = 0，
∴将m,$\frac{1}{n}$看成是一元二次方程ax²+bx + c = 0的两个根.
∵b²-4ac = 0，
∴方程ax²+bx + c = 0有两个相等的实数根，
∴m = $\frac{1}{n}$，即mn = 1.
(3)满足条件的所有k的值为121,242,363,484.
∵m + n = -2，mn = 1，
∴m = -1，n = -1，
∴a - b + c = 0，
∴b = a + c.
∵b²=4ac，
∴(a + c)²=4ac，解得a = c，
∴满足条件的所有k的值为121,242,363,484.