第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2024 内蒙古通辽中考]如图,$□ ABCD的对角线AC$,$BD交于点O$,以下条件不能证明$□ ABCD$是菱形的是( )
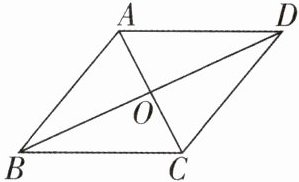
A.$∠BAC = ∠BCA$
B.$∠ABD = ∠CBD$
C.$OA^{2} + OD^{2} = AD^{2}$
D.$AD^{2} + OA^{2} = OD^{2}$

A.$∠BAC = ∠BCA$
B.$∠ABD = ∠CBD$
C.$OA^{2} + OD^{2} = AD^{2}$
D.$AD^{2} + OA^{2} = OD^{2}$
答案:
D 【解析】
∵ ∠BAC = ∠BCA,
∴ AB = BC,
∴ □ABCD 是菱形,故选项 A 不符合题意.
∵ 四边形 ABCD 是平行四边形,
∴ AD//BC,
∴ ∠ADB = ∠CBD.
∵ ∠ABD = ∠CBD,
∴ ∠ABD=∠ADB,
∴ AB=AD,
∴ □ABCD 是菱形,故选项 B 不符合题意.
∵ OA²+OD² = AD²,
∴ ∠AOD = 90°,
∴ AC⊥BD,
∴ □ABCD 是菱形,故选项 C 不符合题意.
∵ AD²+OA² = OD²,
∴ ∠OAD=90°,
∴ OA⊥AD,不能证得□ABCD 是菱形,故选项 D 符合题意.故选 D.
∵ ∠BAC = ∠BCA,
∴ AB = BC,
∴ □ABCD 是菱形,故选项 A 不符合题意.
∵ 四边形 ABCD 是平行四边形,
∴ AD//BC,
∴ ∠ADB = ∠CBD.
∵ ∠ABD = ∠CBD,
∴ ∠ABD=∠ADB,
∴ AB=AD,
∴ □ABCD 是菱形,故选项 B 不符合题意.
∵ OA²+OD² = AD²,
∴ ∠AOD = 90°,
∴ AC⊥BD,
∴ □ABCD 是菱形,故选项 C 不符合题意.
∵ AD²+OA² = OD²,
∴ ∠OAD=90°,
∴ OA⊥AD,不能证得□ABCD 是菱形,故选项 D 符合题意.故选 D.
2 [2024 福建中考]如图,在菱形$ABCD$中,点$E$,$F分别在边BC和CD$上,且$∠AEB = ∠AFD$。求证:$BE = DF$。
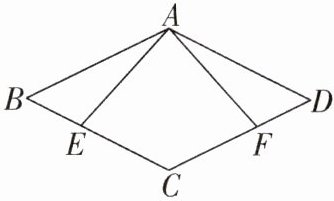

答案:
【证明】
∵ 四边形 ABCD 是菱形,
∴ AB = AD,∠B=∠D.在△ABE 和△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD,
∴ △ABE≌△ADF(AAS),
∴ BE = DF.
∵ 四边形 ABCD 是菱形,
∴ AB = AD,∠B=∠D.在△ABE 和△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD,
∴ △ABE≌△ADF(AAS),
∴ BE = DF.
3 [2024 河北中考]在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”。如图,矩形$ABCD$位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( )
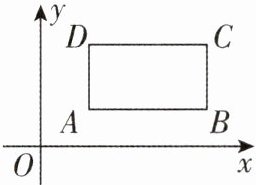
A.点$A$
B.点$B$
C.点$C$
D.点$D$

A.点$A$
B.点$B$
C.点$C$
D.点$D$
答案:
B 【解析】设 A(a,b),AB=m,AD=n.
∵ 四边形 ABCD 为矩形,
∴ AD = BC = n,AB = CD = m,
∴ D(a,b+n),B(a+m,b),C(a+m,b+n).
∵ b/(a+m) < b/a < (b+n)/a,且 b/(a+m) < (b+n)/(a+m),
∴ 该矩形四个顶点中“特征值”最小的是点 B.故选 B.
∵ 四边形 ABCD 为矩形,
∴ AD = BC = n,AB = CD = m,
∴ D(a,b+n),B(a+m,b),C(a+m,b+n).
∵ b/(a+m) < b/a < (b+n)/a,且 b/(a+m) < (b+n)/(a+m),
∴ 该矩形四个顶点中“特征值”最小的是点 B.故选 B.
4 [2024 甘肃兰州中考]如图,在$\triangle ABC$中,$AB = AC$,$D是BC$的中点,$CE// AD$,$AE⊥AD$,$EF⊥AC$。
(1)求证:四边形$ADCE$是矩形;
(2)若$BC = 4$,$CE = 3$,求$EF$的长。
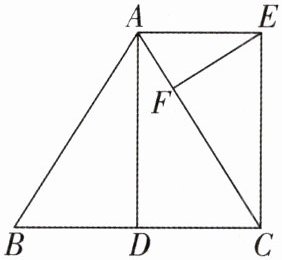
(1)求证:四边形$ADCE$是矩形;
(2)若$BC = 4$,$CE = 3$,求$EF$的长。

答案:
(1)【证明】
∵ 在△ABC 中,AB = AC,D 是 BC 的中点,
∴ AD⊥BC,即∠ADC = ∠ADB = 90°.
∵ CE//AD,
∴ ∠ECD = ∠ADB = 90°.
∵ AE⊥AD,
∴ ∠EAD = 90°,
∴ ∠ADC = ∠ECD = ∠EAD=90°,
∴ 四边形 ADCE 是矩形.
(2)【解】
∵ 在△ABC 中,AB = AC,D 是 BC 的中点,BC = 4,
∴ BD = CD = 1/2 BC = 2.由
(1)可知,四边形 ADCE 是矩形,
∴ AE = CD = 2,∠AEC=90°.在 Rt△AEC 中,AE = 2,CE = 3,
∴ 由勾股定理得 AC = √(AE²+CE²) = √13.
∵ EF⊥AC,
∴ S_△AEC = 1/2 AC·EF = 1/2 AE·CE,
∴ EF = (AE·CE)/AC = (2×3)/√13 = 6√13/13.
(1)【证明】
∵ 在△ABC 中,AB = AC,D 是 BC 的中点,
∴ AD⊥BC,即∠ADC = ∠ADB = 90°.
∵ CE//AD,
∴ ∠ECD = ∠ADB = 90°.
∵ AE⊥AD,
∴ ∠EAD = 90°,
∴ ∠ADC = ∠ECD = ∠EAD=90°,
∴ 四边形 ADCE 是矩形.
(2)【解】
∵ 在△ABC 中,AB = AC,D 是 BC 的中点,BC = 4,
∴ BD = CD = 1/2 BC = 2.由
(1)可知,四边形 ADCE 是矩形,
∴ AE = CD = 2,∠AEC=90°.在 Rt△AEC 中,AE = 2,CE = 3,
∴ 由勾股定理得 AC = √(AE²+CE²) = √13.
∵ EF⊥AC,
∴ S_△AEC = 1/2 AC·EF = 1/2 AE·CE,
∴ EF = (AE·CE)/AC = (2×3)/√13 = 6√13/13.
5 [2024 重庆中考 B 卷]如图,在边长为 4 的正方形$ABCD$中,点$E是BC$上一点,点$F是CD$延长线上一点,连接$AE$,$AF$,$AM平分∠EAF交CD于点M$。若$BE = DF = 1$,则$DM$的长度为( )
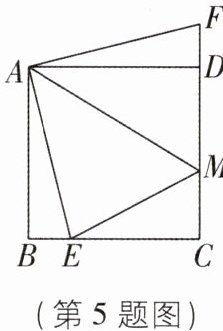
A.2
B.$\sqrt{5}$
C.$\sqrt{6}$
D.$\frac{12}{5}$

A.2
B.$\sqrt{5}$
C.$\sqrt{6}$
D.$\frac{12}{5}$
答案:
D 【解析】
∵ 四边形 ABCD 是正方形,
∴ AB = AD,∠ABE = ∠ADF = 90°.在△ABE 和△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD,
∴ △ABE≌△ADF(SAS),
∴ AE = AF.
∵ AM 平分∠EAF,
∴ ∠EAM = ∠FAM.在△AEM 和△AFM 中,{AE=AF,∠EAM=∠FAM,AM=AM,
∴ △AEM≌△AFM(SAS),
∴ EM=FM.
∵ 四边形 ABCD 是边长为 4 的正方形,
∴ BC=CD=4,∠BCD=90°,
∴ CE = BC - BE=4-1=3.设 DM = x,则 MC = CD - DM = 4 - x,EM = FM = FD + DM = 1 + x.在 Rt△MCE 中,根据勾股定理,得 EM² = MC² + CE²,即(1 + x)²=(4 - x)² + 3²,解得 x = 12/5.故选 D.
∵ 四边形 ABCD 是正方形,
∴ AB = AD,∠ABE = ∠ADF = 90°.在△ABE 和△ADF 中,{∠B=∠D,∠AEB=∠AFD,AB=AD,
∴ △ABE≌△ADF(SAS),
∴ AE = AF.
∵ AM 平分∠EAF,
∴ ∠EAM = ∠FAM.在△AEM 和△AFM 中,{AE=AF,∠EAM=∠FAM,AM=AM,
∴ △AEM≌△AFM(SAS),
∴ EM=FM.
∵ 四边形 ABCD 是边长为 4 的正方形,
∴ BC=CD=4,∠BCD=90°,
∴ CE = BC - BE=4-1=3.设 DM = x,则 MC = CD - DM = 4 - x,EM = FM = FD + DM = 1 + x.在 Rt△MCE 中,根据勾股定理,得 EM² = MC² + CE²,即(1 + x)²=(4 - x)² + 3²,解得 x = 12/5.故选 D.
6 新考向开放性试题 [2024 黑龙江龙东地区中考]如图,在菱形$ABCD$中,对角线$AC$,$BD相交于点O$,请添加一个条件____,使得菱形$ABCD$为正方形。
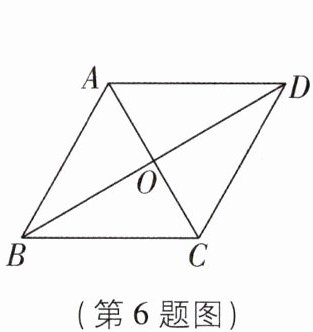

答案:
AC = BD(答案不唯一) 【解析】添加 AC = BD.
∵ 四边形 ABCD 是菱形,AC = BD,
∴ 菱形 ABCD 为正方形.故答案为 AC = BD(答案不唯一).
∵ 四边形 ABCD 是菱形,AC = BD,
∴ 菱形 ABCD 为正方形.故答案为 AC = BD(答案不唯一).
7 [2024 江苏徐州中考]已知:如图,四边形$ABCD$为正方形,点$E在BD$的延长线上,连接$EA$,$EC$。
(1)求证:$\triangle EAB\cong\triangle ECB$;
(2)若$∠AEC = 45^{\circ}$,求证:$DC = DE$。
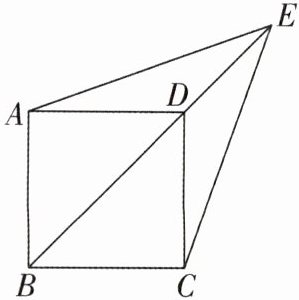
(1)求证:$\triangle EAB\cong\triangle ECB$;
(2)若$∠AEC = 45^{\circ}$,求证:$DC = DE$。

答案:
(1)【证明】
∵ 四边形 ABCD 为正方形,
∴ AB = BC,∠ABE = ∠CBE = 45°.在△EAB 和△ECB 中,{AB=BC,∠ABE=∠CBE,BE=BE,
∴ △EAB≌△ECB(SAS).
(2)【证明】
∵ 四边形 ABCD 为正方形,
∴ ∠BDC = 1/2 ∠CDA = 45°.
∵ △EAB≌△ECB,∠AEC = 45°,
∴ ∠CED = ∠AED = 1/2 ∠AEC = 22.5°.
∵ ∠BDC = ∠CED + ∠DCE = 45°,
∴ ∠DCE = 45° - 22.5° = 22.5°,
∴ ∠CED = ∠DCE,
∴ DC = DE.
(1)【证明】
∵ 四边形 ABCD 为正方形,
∴ AB = BC,∠ABE = ∠CBE = 45°.在△EAB 和△ECB 中,{AB=BC,∠ABE=∠CBE,BE=BE,
∴ △EAB≌△ECB(SAS).
(2)【证明】
∵ 四边形 ABCD 为正方形,
∴ ∠BDC = 1/2 ∠CDA = 45°.
∵ △EAB≌△ECB,∠AEC = 45°,
∴ ∠CED = ∠AED = 1/2 ∠AEC = 22.5°.
∵ ∠BDC = ∠CED + ∠DCE = 45°,
∴ ∠DCE = 45° - 22.5° = 22.5°,
∴ ∠CED = ∠DCE,
∴ DC = DE.
查看更多完整答案,请扫码查看


