第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1 [2025 安徽六安期末] 下列多边形一定相似的是 ( )
A.两个等腰三角形
B.两个平行四边形
C.两个正五边形
D.两个六边形
A.两个等腰三角形
B.两个平行四边形
C.两个正五边形
D.两个六边形
答案:
1.C [解析]两个等腰三角形,各角不一定对应相等,各边不一定成比例,所以不一定相似,故A不正确;两个平行四边形,各角不一定对应相等,各边不一定成比例,所以不一定相似,故B不正确;两个正五边形,各角分别相等,各边成比例,所以相似,故C正确;两个正六边形相似,但是两个六边形不一定相似,故D不正确.故选C.
2 [2024 江苏连云港中考改编] 下列网格中各个小正方形的边长均为 1, 阴影部分图形分别记作甲、乙、丙、丁, 其中是相似多边形的为 ( )
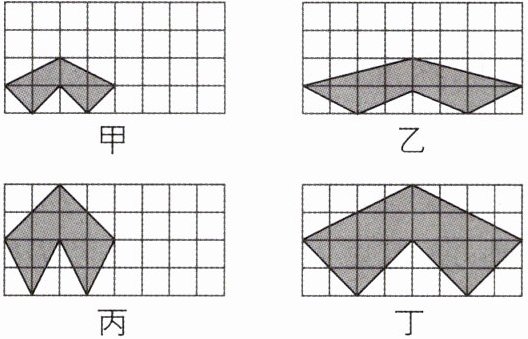
A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁

A.甲和乙
B.乙和丁
C.甲和丙
D.甲和丁
答案:
2.D [解析]观察可得甲和丁各角分别相等,各边成比例,所以甲和丁是相似多边形.故选D.
3 如图, 四边形 $ABCD \backsim$ 四边形 $EFGH$, $\angle A = 80^{\circ}$, $\angle C = 90^{\circ}$, $\angle F = 70^{\circ}$, 则 $\angle H$ 等于 ( )
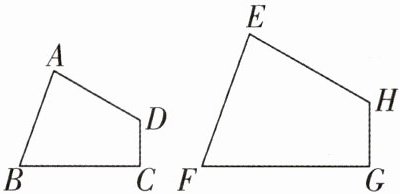
A.$70^{\circ}$
B.$80^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$

A.$70^{\circ}$
B.$80^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
答案:
3.D [解析]
∵四边形ABCD∽四边形EFGH,∠A = 80°,∠C = 90°,∠F = 70°,
∴∠E = ∠A = 80°,∠G = ∠C = 90°,
∴∠H = 360° - ∠E - ∠F - ∠G = 360° - 80° - 70° - 90° = 120°.故选D.
∵四边形ABCD∽四边形EFGH,∠A = 80°,∠C = 90°,∠F = 70°,
∴∠E = ∠A = 80°,∠G = ∠C = 90°,
∴∠H = 360° - ∠E - ∠F - ∠G = 360° - 80° - 70° - 90° = 120°.故选D.
4 [2025 宁夏吴忠校级质检] 如图, 正五边形 $FGHMN$ 和正五边形 $ABCDE$ 相似, 若 $AB : FG = 2 : 3$, 则下列结论正确的是 ( )

A.$2DE = 3MN$
B.$3DE = 2MN$
C.$3\angle A = 2\angle F$
D.$2\angle A = 3\angle F$

A.$2DE = 3MN$
B.$3DE = 2MN$
C.$3\angle A = 2\angle F$
D.$2\angle A = 3\angle F$
答案:
4.B [解析]
∵正五边形FGHMN和正五边形ABCDE相似,
∴DE:MN = AB:FG = 2:3,∠F = ∠A,
∴3DE = 2MN.故选B.
∵正五边形FGHMN和正五边形ABCDE相似,
∴DE:MN = AB:FG = 2:3,∠F = ∠A,
∴3DE = 2MN.故选B.
5 [2024 山东枣庄调研] 如图, 矩形 $ABCD$ 中, $AD$ 为较长边, $AB = 1$, 在 $BC$ 上取一点 $E$, 沿 $AE$ 将 $\triangle ABE$
向上折叠, 使点 $B$ 落在 $AD$ 上的点 $F$ 处, 若四边形 $EFDC$ 与矩形 $ABCD$ 相似, 则 $AD = $ ____.
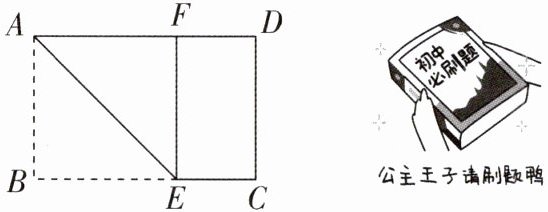
向上折叠, 使点 $B$ 落在 $AD$ 上的点 $F$ 处, 若四边形 $EFDC$ 与矩形 $ABCD$ 相似, 则 $AD = $ ____.

答案:
5.$\frac{1+\sqrt{5}}{2}$
思路分析

[解析]
∵沿AE将△ABE向上折叠,使点B落在AD上的点F处,AB = 1,
∴易知AF = EF = 1.设AD = x,则FD = x - 1.
∵四边形EFDC与矩形ABCD相似,
∴$\frac{EF}{FD}=\frac{AD}{AB}$,即$\frac{1}{x - 1}=\frac{x}{1}$,解得$x_1=\frac{1+\sqrt{5}}{2}$,$x_2=\frac{1 - \sqrt{5}}{2}$(舍去),经检验$x=\frac{1+\sqrt{5}}{2}$是原方程的解.故答案为$\frac{1+\sqrt{5}}{2}$.
5.$\frac{1+\sqrt{5}}{2}$
思路分析

[解析]
∵沿AE将△ABE向上折叠,使点B落在AD上的点F处,AB = 1,
∴易知AF = EF = 1.设AD = x,则FD = x - 1.
∵四边形EFDC与矩形ABCD相似,
∴$\frac{EF}{FD}=\frac{AD}{AB}$,即$\frac{1}{x - 1}=\frac{x}{1}$,解得$x_1=\frac{1+\sqrt{5}}{2}$,$x_2=\frac{1 - \sqrt{5}}{2}$(舍去),经检验$x=\frac{1+\sqrt{5}}{2}$是原方程的解.故答案为$\frac{1+\sqrt{5}}{2}$.
6 如图, 四边形 $ABCD$ 和四边形 $EFGH$ 相似 (点 $A$ 与点 $E$, 点 $B$ 与点 $F$, 点 $C$ 与点 $G$, 点 $D$ 与点 $H$ 分别是对应点), 且顶点都在方格纸的格点上, 它们的相似比是 ( )

A.$1 : 2$
B.$1 : 4$
C.$2 : 1$
D.$4 : 1$

A.$1 : 2$
B.$1 : 4$
C.$2 : 1$
D.$4 : 1$
答案:
6.C [解析]设方格纸上每个小正方形的边长为1,则$AD = 2\sqrt{2}$,$HE = \sqrt{2}$.
∵四边形ABCD和四边形EFGH相似,
∴相似比为AD:EH = $2\sqrt{2}:\sqrt{2}=2:1$.故选C.
∵四边形ABCD和四边形EFGH相似,
∴相似比为AD:EH = $2\sqrt{2}:\sqrt{2}=2:1$.故选C.
7 把一个正多边形的边长扩大到原来的 $2.5$ 倍, 则原图与新图的相似比为 ____.
答案:
7.2:5 [解析]
∵把一个正多边形的边长扩大到原来的2.5倍,设原边长为1,则扩大后的边长为2.5,
∴原图与新图的相似比为1:2.5,即2:5.
∵把一个正多边形的边长扩大到原来的2.5倍,设原边长为1,则扩大后的边长为2.5,
∴原图与新图的相似比为1:2.5,即2:5.
8 如图, 一块矩形草坪长 $30$ m, 宽 $20$ m, 外围有等宽 (宽度为 $2$ m) 的小路.
(1) 内外两个矩形相似吗?
(2) 要使内外两个矩形相似, 相邻两条小路的宽度不相等, 并且相对两条小路的宽度相等, 仍保证外矩形的横向边为较长边, 求相邻两条小路宽度的比值.
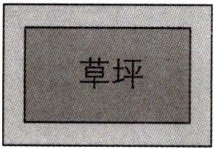
(1) 内外两个矩形相似吗?
(2) 要使内外两个矩形相似, 相邻两条小路的宽度不相等, 并且相对两条小路的宽度相等, 仍保证外矩形的横向边为较长边, 求相邻两条小路宽度的比值.

答案:
8.[解]
(1)不相似.因为内矩形的长、宽分别为30m,20m,小路宽2m,则外矩形的长、宽分别为34m,24m,而$\frac{30}{20}≠\frac{34}{24}$,所以对应边不成比例,所以内外两个矩形不相似.
(2)如图,设相邻两条小路的宽度分别是xm和ym.
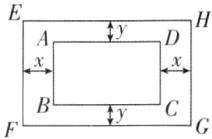
∵相对两条小路的宽度相等,
∴EF = AB + 2y = (20 + 2y)m,EH = AD + 2x = (30 + 2x)m.
∵矩形EFGH与矩形ABCD相似,
∴$\frac{EF}{AB}=\frac{EH}{AD}$,
∴$\frac{20 + 2y}{20}=\frac{30 + 2x}{30}$,
∴$\frac{x}{y}=\frac{3}{2}$,
∴相邻两条小路宽度的比值为$\frac{3}{2}$(或$\frac{2}{3}$).
8.[解]
(1)不相似.因为内矩形的长、宽分别为30m,20m,小路宽2m,则外矩形的长、宽分别为34m,24m,而$\frac{30}{20}≠\frac{34}{24}$,所以对应边不成比例,所以内外两个矩形不相似.
(2)如图,设相邻两条小路的宽度分别是xm和ym.

∵相对两条小路的宽度相等,
∴EF = AB + 2y = (20 + 2y)m,EH = AD + 2x = (30 + 2x)m.
∵矩形EFGH与矩形ABCD相似,
∴$\frac{EF}{AB}=\frac{EH}{AD}$,
∴$\frac{20 + 2y}{20}=\frac{30 + 2x}{30}$,
∴$\frac{x}{y}=\frac{3}{2}$,
∴相邻两条小路宽度的比值为$\frac{3}{2}$(或$\frac{2}{3}$).
查看更多完整答案,请扫码查看


