《2025年初中必刷题九年级数学上册北师大版》

1 下列各选项中的两个相似图形不是位似图形的是 ( )

答案： D　[解析]只有选项D中的对应点的连线所在的直线不会相交于一点.故选D.

2 如图,在正方形网格中,$△ABC和△DEF$位似,则关于位似中心与相似比叙述正确的是( )

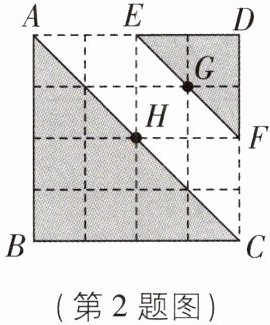
A.位似中心是点 B,相似比是$2:1$
B.位似中心是点 D,相似比是$2:1$
C.位似中心在点 G,H 之间,相似比为$2:1$
D.位似中心在点 G,H 之间,相似比为$1:2$

答案：
C　[解析]如图,在正方形网格中，△ABC和△DEF位似， 连接AF,CE,BD,可知位似中心在点G,H之间.又
∵AC=2EF,
∴相似比为2:1.

3 [2025浙江丽水校级质检]如图,在由若干个边长相等的小正方形组成的网格中,以点O为位似中心,四边形ABCD的位似图形是 ( )

A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR

答案： A　[解析]设网格中每个小正方形的边长为1,则AB=AD=DC=CB=$\sqrt{5}$,MQ=MP=PN=NQ=2$\sqrt{5}$,
∴$\frac{AB}{NP}$=$\frac{AD}{NQ}$=$\frac{DC}{MQ}$=$\frac{CB}{PM}$=$\frac{1}{2}$,四边形ABCD与四边形NPMQ都是菱形.又
∵由题图易知两菱形各角对应相等，
∴两菱形相似.又
∵A和N,B和P,C和M,D和Q所在的直线相交于点O,
∴以点O为位似中心，四边形ABCD的位似图形是四边形NPMQ.故选A.

4 [2025四川眉山质检]如图,四边形ABCD和$A'B'C'D'$是以点O为位似中心的位似图形.若$OA':A'A= 2:1$,四边形$A'B'C'D'的面积为12cm^{2}$,则四边形ABCD的面积为 ( )

A.$24cm^{2}$
B.$27cm^{2}$
C.$36cm^{2}$
D.$54cm^{2}$

答案： B　[解析]
∵四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形,OA':A'A=2:1，
∴OA':OA=2:3,
∴易知四边形ABCD与四边形A'B'C'D'的相似比为3:2,
∴面积比为9:4.又
∵四边形A'B'C'D'的面积为12cm²,
∴四边形ABCD的面积为27cm².故选B.

5 如图,$△ABC与△DEF$位似,点O是它们的位似中心,其中$OC:CF= 1:2$,则$△ABC和△DEF$的周长之比是 ( )

A.$1:2$
B.$1:3$
C.$1:4$
D.$1:9$

答案： B　[解析]
∵OC:CF=1:2,
∴OC:OF=1:3.
∵△ABC与△DEF位似，
∴AC//DF,△ABC∽△DEF,
∴易证△AOC∽△DOF,
∴$\frac{AC}{DF}$=$\frac{OC}{OF}$=$\frac{1}{3}$,
∴△ABC与△DEF的周长之比为1:3,故选B.

6 如图,以点O为位似中心,把$△ABC$放大为原来的2倍得到$△A'B'C'$,以下说法正确的是______.(填序号)
①$S_{△ABC}:S_{△A'B'C'}= 1:2$;②$AB:A'B'= 1:2$;③点A,O,$A'$在同一条直线上;④$BC// B'C'.$

答案： ②③④　[解析]以点O为位似中心,把△ABC放大为原来的2倍得到△A'B'C',则点A,O,A'在同一条直线上,BC//B'C',△ABC∽△A'B'C',且相似比为1:2,
∴AB:A'B'=1:2,S△ABC:S△A'B'C'=1:4,故①说法错误,②③④说法正确.

7 [2025河南洛阳期中]如图,在网格中,每个小正方形的边长都是1,$△ABC与△A'B'C'$是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)在网格中画出位似中心O.(要求保留画图痕迹)
(2)$△ABC与△A'B'C'$的相似比是______.
(3)在网格中,以点C为位似中心,画出$△A_{1}B_{1}C$,使它与$△ABC$位似,且相似比等于2.

答案：
[解]
(1)如图
(1)所示,点O即为位似中心.
(2)
∵B'C'=$\sqrt{2^2+4^2}$=2$\sqrt{5}$,BC=$\sqrt{2^2+1^2}$=$\sqrt{5}$,
∴$\frac{BC}{B'C'}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$,
∴△ABC与△A'B'C'的相似比是$\frac{1}{2}$.故答案为$\frac{1}{2}$.
(3)如图
(2)所示,△ABC即为所求.