第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1如图,在△ABC中,AB= AC,点D在BC边上,DF//AB,DE//AC,则当∠B= ______°时,四边形AEDF是矩形.
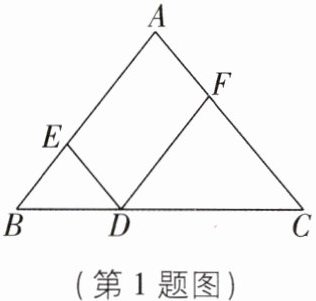

答案:
45
2[2024山东威海文登区期末]如图,矩形ABCD中,对角线AC,BD交于点O,过点O的直线EF分别交AB,CD于点E,F,若AB= 6,BC= 8,则图中阴影部分的面积为______.
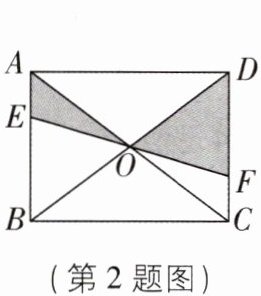

答案:
12
3[2024湖北武汉调研]两个矩形的位置如图所示,若∠1= α,则∠2= ( )
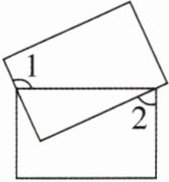
A.α-90°
B.180°-α
C.α-45°
D.270°-α

A.α-90°
B.180°-α
C.α-45°
D.270°-α
答案:
B
4[2024广西南宁质检]如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE= DF.
(1)求证:AE= CF;
(2)若AB= 6,∠COD= 60°,求矩形ABCD的面积.
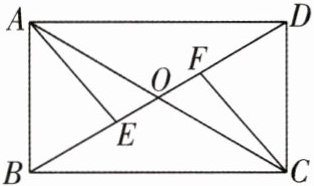
(1)求证:AE= CF;
(2)若AB= 6,∠COD= 60°,求矩形ABCD的面积.

答案:
(1)【证明】
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,
∴OE=OF.在△AOE和△COF中,$\left\{\begin{array}{l} OA=OC,\\ ∠AOE=∠COF,\\ OE=OF,\end{array}\right. $
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)【解】
∵OA=OC,OB=OD,AC=BD,
∴OA=OB.
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
∴OA=AB=6,
∴AC=2OA=12.在Rt△ABC中,BC=$\sqrt{AC^2 - AB^2}$=$6\sqrt{3}$,
∴矩形ABCD的面积为AB·BC=$6×6\sqrt{3}$=$36\sqrt{3}$.
(1)【证明】
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,
∴OE=OF.在△AOE和△COF中,$\left\{\begin{array}{l} OA=OC,\\ ∠AOE=∠COF,\\ OE=OF,\end{array}\right. $
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)【解】
∵OA=OC,OB=OD,AC=BD,
∴OA=OB.
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
∴OA=AB=6,
∴AC=2OA=12.在Rt△ABC中,BC=$\sqrt{AC^2 - AB^2}$=$6\sqrt{3}$,
∴矩形ABCD的面积为AB·BC=$6×6\sqrt{3}$=$36\sqrt{3}$.
5[2025陕西宝鸡质检]如图,一架梯子AB斜靠在一竖直的墙OP上,OA= 12m,OB= 5m.若梯子顶端A沿墙下滑a m到A'的位置,则此时梯子的中点M'到墙角O的距离为 ( )
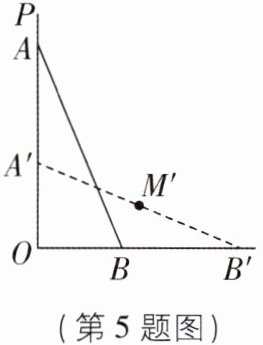
A.5.5m
B.6m
C.6.5m
D.7m

A.5.5m
B.6m
C.6.5m
D.7m
答案:
C
6[2025宁夏吴忠校级质检]如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB= 5,AD= 12,则四边形ABOM的周长为 ( )
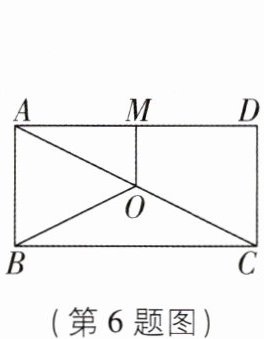
A.17
B.18
C.19
D.20

A.17
B.18
C.19
D.20
答案:
D
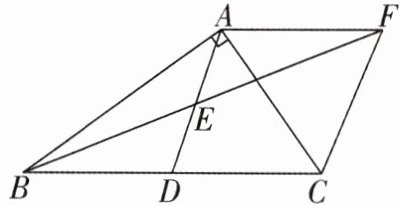
7[2024江苏扬州质检]如图,在Rt△ABC中,∠BAC= 90°,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形.

答案:
(1)【证明】
∵AF//BC,
∴∠AFE=∠DBE.
∵E是AD的中点,
∴AE=DE.在△AFE和△DBE中,$\left\{\begin{array}{l} ∠AFE=∠DBE,\\ ∠FEA=∠BED,\\ AE=DE,\end{array}\right. $
∴△AFE≌△DBE(AAS).
(2)【证明】由
(1)知,△AFE≌△DBE,则AF=DB.
∵D是BC的中点,
∴DB=DC,
∴AF=CD.
∵AF//BC,
∴四边形ADCF是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=DC=$\frac{1}{2}$BC,
∴四边形ADCF是菱形.
(1)【证明】
∵AF//BC,
∴∠AFE=∠DBE.
∵E是AD的中点,
∴AE=DE.在△AFE和△DBE中,$\left\{\begin{array}{l} ∠AFE=∠DBE,\\ ∠FEA=∠BED,\\ AE=DE,\end{array}\right. $
∴△AFE≌△DBE(AAS).
(2)【证明】由
(1)知,△AFE≌△DBE,则AF=DB.
∵D是BC的中点,
∴DB=DC,
∴AF=CD.
∵AF//BC,
∴四边形ADCF是平行四边形.
∵∠BAC=90°,D是BC的中点,
∴AD=DC=$\frac{1}{2}$BC,
∴四边形ADCF是菱形.
查看更多完整答案,请扫码查看


