《2025年初中必刷题九年级数学上册北师大版》

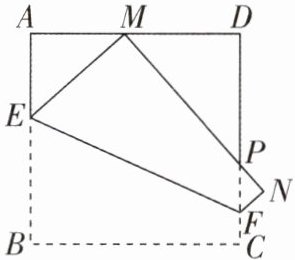
1 [2024江苏连云港调研,中]如图,将边长为12cm的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.若AM= 5cm,则折痕EF的长为______cm.

答案：
13 【解析】如图,过点F作FG⊥AB,垂足为G,连接BM.
∵ 四边形ABCD是正方形,
∴ AB=BC.易知四边形BCFG是矩形,
∴ FG=BC,
∴ AB=FG.
∵ 由折叠易知BM⊥FE,
∴ ∠EBM+∠BEF=90°.
∵ ∠BMA+∠EBM=90°,
∴ ∠BEF=∠BMA.又
∵ ∠A=∠EGF=90°,
∴ △ABM≌△GFE,
∴ EF=BM=$\sqrt{AB^2+AM^2}=\sqrt{12^2+5^2}=13$(cm).故答案为13.

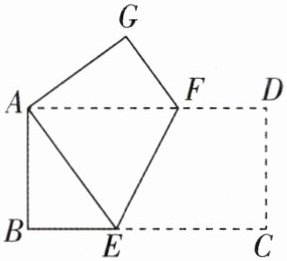
2 [2025浙江金华质检,中]如图,在菱形ABCD中,点E,F分别在AB,BC上,沿EF翻折后,点B落在边CD上的G处,若EG⊥CD,BE= 4,DG= 3,则AE的长为______.

答案：
$\frac{9}{14}$ 【解析】如图,作BH⊥CD交DC的延长线于点H,则∠H=90°.
∵ EG⊥CD,
∴ BH//EG.
∵ 四边形ABCD是菱形,
∴ AB//CD,AB=BC=CD,
∴ BE//GH,
∴ 四边形BEGH是平行四边形,
∴ BH=GE,GH=BE=4.由翻折得GE=BE=4,
∴ BH=GE=4.
∵ DG=3,
∴ DH=DG+GH=3+4=7.
∵ BH²+CH²=BC²,CH=7 - CD=7 - AB,
∴ 4²+(7 - AB)²=AB²,解得AB=$\frac{65}{14}$,
∴ AE=AB - BE=$\frac{65}{14}-4=\frac{9}{14}$,故答案为$\frac{9}{14}$.

3 [2025上海浦东新区质检,中]如图,在正方形ABCD的边AB上取一点E,连接CE,将△BCE沿CE翻折,点B恰好与对角线AC上的点F重合,连接DF,若BE= 2,则△CDF的面积是______.

答案：
$3\sqrt{2}+4$ 【解析】如图,连接BD交AC于O.
∵ 四边形ABCD为正方形,
∴ ∠ABC=90°,AB=BC,AC⊥BD,DO=BO,
∴ ∠BAC=45°.
∵ △BCE沿CE翻折,
∴ BE=EF=2,BC=CF,∠EFC=∠ABC=90°,
∴ ∠AEF=45°,
∴ AF=EF=2,
∴ AE=$2\sqrt{2}$,
∴ AB=$2\sqrt{2}+2$=BC=CF=CD,
∴ BD=$4+2\sqrt{2}$,
∴ OD=$2+\sqrt{2}$,
∴ $S_{\triangle CDF}=\frac{1}{2}× CF× DO=3\sqrt{2}+4$.故答案为$3\sqrt{2}+4$.

4 [2025江苏徐州调研,中]如图,将一张矩形纸片ABCD沿EF折叠,使C,A两点重合,点D落在点G处.已知AB= 4,BC= 8.
(1)求证:△AEF是等腰三角形;
(2)求线段FD的长.

答案：
(1)【证明】由折叠可知,∠AEF=∠CEF.由矩形性质可得AD//BC,
∴ ∠AFE=∠CEF,
∴ ∠AEF=∠AFE,
∴ AE=AF,
∴ △AEF为等腰三角形
(2)【解】由折叠可得AE=CE.设CE=x=AE,则BE=BC - CE=8 - x.
∵ ∠B=90°,
∴ 在Rt△ABE中,AB²+BE²=AE²,即4²+(8 - x)²=x²,解得x=5.由
(1)可得AF=AE=5,
∴ FD=AD - AF=BC - AF=8 - 5=3.

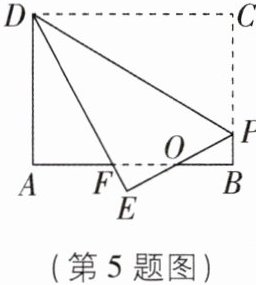
5 [2025重庆沙坪坝区质检,中]如图,矩形纸片ABCD中,AB= 4,BC= 3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP= OF,则BF的长为( )

A.1
B.2
C.3
D.2.4

答案： D 【解析】
∵ 矩形纸片ABCD中,BC=3,AB=4,
∴ ∠B=∠A=∠C=90°,BC=AD=3,AB=DC=4.根据折叠可知△DCP≌△DEP,
∴ DC=DE=4,∠E=∠C=90°,CP=EP,
方法总结：6.C 翻折问题常利用图形本身的性质、全等三角形、勾股定理、方程思想等知识求解,矩形中折叠必出等腰三角形:平行+角平分线(折叠)⇒等腰三角形
∴ ∠E=∠B=90°.在△OBP和△OEF中,$\left\{\begin{array}{l} ∠B=∠E,\\ ∠BOP=∠EOF,\\ OP=OF,\end{array}\right.$
∴ △OBP≌△OEF(AAS),
∴ EF=BP,OE=OB,
∴ BF=OB+OF=OE+OP=PE,
∴ BF=EP=CP.设BF=EP=CP=x,则AF=4 - x,BP=3 - x=EF,
∴ DF=DE - EF=4-(3 - x)=x + 1.
∵ ∠A=90°,
∴ Rt△ADF中,AF²+AD²=DF²,即(4 - x)²+3²=(1 + x)²,解得x=$\frac{12}{5}$,
∴ BF=$\frac{12}{5}=2.4$,故选D.

6 [2025浙江杭州期末,较难]如图,矩形ABCD中,AB= 4,BC= 8,点E是边BC上一动点,沿AE翻折,若点B的对应点B'恰好落在矩形的对称轴上,则折痕AE的长是( )

A.$\frac{8\sqrt{3}}{3}$
B.$\frac{4\sqrt{3}}{3}$
C.$4\sqrt{2}或\frac{8\sqrt{3}}{3}$
D.$4\sqrt{2}或\frac{4\sqrt{3}}{3}$

答案：
C 【解析】分两种情况:①如图
(1)所示,当B'恰好在矩形的对称轴MN上时,易知点B'与点M重合,点E与点N重合.
∵ AB=4,BE=$\frac{1}{2}BC=4$,
∴ AE=$\sqrt{AB^2+BE^2}=\sqrt{4^2+4^2}=4\sqrt{2}$.②如图
(2)所示,当B'恰好在矩形的对称轴GH上时,过B'作PQ//AB交AD于P,交BC于Q,
∴ PQ⊥AD,PQ⊥BC,PB'=QB'=$\frac{1}{2}PQ=\frac{1}{2}AB=2$,AP=BQ.
∵ 四边形ABCD是矩形,
∴ ∠B=90°.由折叠的性质得AB'=AB=4,BE=B'E.在Rt△APB'中,AP=$\sqrt{AB'^2-PB'^2}=\sqrt{4^2-2^2}=2\sqrt{3}$,
∴ BQ=AP=$2\sqrt{3}$.设BE=B'E=x,则EQ=BQ - BE=$2\sqrt{3}-x$.在Rt△EB'Q中,EQ²+B'Q²=B'E²,
∴ $(2\sqrt{3}-x)^2+2^2=x^2$,解得x=$\frac{4\sqrt{3}}{3}$,即BE=$\frac{4\sqrt{3}}{3}$,
∴ AE=$\sqrt{AB^2+BE^2}=\sqrt{4^2+(\frac{4\sqrt{3}}{3})^2}=\frac{8\sqrt{3}}{3}$.综上所述,当点B'恰好在矩形的对称轴上时,折痕AE的长是$4\sqrt{2}$或$\frac{8\sqrt{3}}{3}$,故选C.

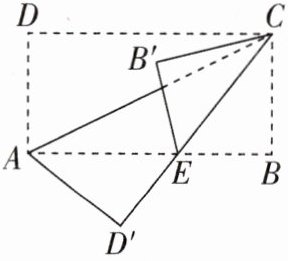
7 [2025江苏南京调研,较难]如图,矩形ABCD的边AD长为2,将△ADC沿对角线AC翻折得到△AD'C,CD'与AB交于点E,再将△BCE沿CE翻折得到△B'CE.若两次折叠后,点B'恰好落在△ADC的边上,则AB的长为______.

答案：
$2\sqrt{3}$或$2\sqrt{2}+2$ 【解析】
∵ 四边形ABCD为矩形,
∴ BC=AD=2,∠B=∠D=90°.
∵ △ADC沿对角线AC翻折得到△AD'C,
∴ ∠D'=∠D=90°,AD'=AD=2.
∵ 将△BCE沿CE翻折得到△B'CE,
∴ ∠CB'E=∠B=90°,CB'=CB=2.
①当点B'恰好落在AC上时,如图
(1).在△AD'E和△CBE中,$\left\{\begin{array}{l} ∠AED'=∠CEB,\\ ∠D'=∠B,\\ AD'=CB,\end{array}\right.$
∴ △AD'E≌△CBE(AAS),
∴ EA=EC,即△EAC为等腰三角形.
∵ ∠CB'E=90°,
∴ 点B'为AC中点,
∴ AC=2CB'=4.在Rt△ABC中,AB²+BC²=AC²,即AB²+2²=4²,解得AB=$2\sqrt{3}$(负值已舍去).
②当点B'恰好落在D'C上时,如图
(2).
∵ ∠AD'C=∠CB'E=90°,
∴ AD'//B'C,
∵ AD'=B'C=2,
∴ 四边形AD'CB'是平行四边形,
∴ AB'=CD'=AB,
∵ ∠DAB=∠CB'E=90°,
∴ 四边形AB'CD'是矩形,
∴ AB'=CD'=AB,AD'=B'C=2,在Rt△CBE 中,CE=$\sqrt{CB^2+BE^2}=\sqrt{2^2+2^2}=2\sqrt{2}$,同①可得△AD'E≌△CBE,
∴ AE=CE=2$\sqrt{2}$,
∴ AB=AE + BE=2$\sqrt{2}+2$.综上所述,AB的长为$2\sqrt{3}$或$2\sqrt{2}+2$.