《2025年初中必刷题九年级数学上册北师大版》

1 [2024 河北邯郸调研]依据所标识的数据判断,下列平行四边形一定为菱形的是 ( )

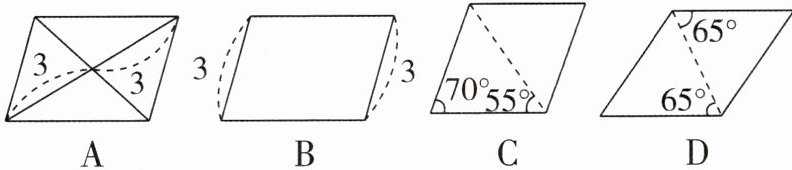
答案： C 【解析】
∵ 四边形是平行四边形，
∴ 对角线互相平分，故 A 不一定是菱形.
∵ 四边形是平行四边形，
∴ 对边相等，故 B 不一定是菱形. 根据三角形的内角和定理可得 $180^\circ -70^\circ -55^\circ =55^\circ$，
∴ 邻边相等.
∵ 四边形是平行四边形，
∴ 该四边形是菱形，故 C 是菱形.
∵ 四边形是平行四边形，
∴ 对边平行，故 D 不一定是菱形. 故选 C.

2 [2025 福建漳州期中]为判断一块地砖是否为菱形,甲、乙二人分别用仪器进行了测量,甲测量出两组对边分别相等,然后乙进行测量,最后得到结论:地砖是菱形,则乙测量的结果是____.(填序号)
①两组对边分别平行;②一组邻边相等;③一组邻角相等.

答案： ② 【解析】
∵ 甲测量出两组对边分别相等，
∴ 该地砖是平行四边形，
∴ 当一组邻边相等时，该地砖是菱形，
∴ 乙测量出一组邻边相等. 故答案为②.

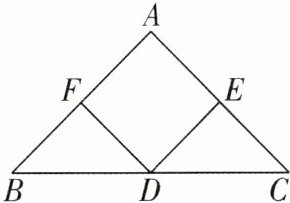
3 新考向开放性试题[2025 黑龙江齐齐哈尔质检]如图,在△ABC 中,点 D,E,F 分别是边 BC,CA,AB 的中点,要使四边形 AFDE 为菱形,应添加的条件是____(添加一个条件即可).

答案： $AB=AC$（答案不唯一）【解析】添加条件：$AB=AC$.
∵ 点 D,E,F 分别是边 BC,CA,AB 的中点，
∴ $DF// AC$, $DE// AB$，
∴ 四边形 AFDE 为平行四边形.
∵ $AB=AC$，
∴ $DF=\frac{1}{2}AC=\frac{1}{2}AB=AF$，
∴ 平行四边形 AFDE 为菱形. 故答案为 $AB=AC$（答案不唯一）.

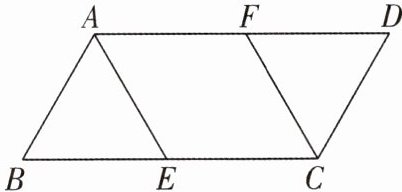
4 如图,平行四边形 ABCD 中,AE,CF 分别是∠BAD,∠BCD 的平分线,且 E,F 分别在边 BC,AD 上,AE= AF.
求证:四边形 AECF 是菱形.

答案： 【证明】
∵ 四边形 ABCD 是平行四边形，
∴ $\angle BAD=\angle BCD$, $AD// BC$.
∵ AE,CF 分别是 $\angle BAD$, $\angle BCD$ 的平分线，
∴ $\angle BAE=\angle DAE=\frac{1}{2}\angle BAD$, $\angle BCF=\angle DCF=\frac{1}{2}\angle BCD$，
∴ $\angle DAE=\angle BCF$.
∵ $AD// BC$，
∴ $\angle DAE=\angle AEB$，
∴ $\angle BCF=\angle AEB$，
∴ $AE// FC$，
∴ 四边形 AECF 是平行四边形.
∵ $AE=AF$，
∴ 四边形 AECF 是菱形.

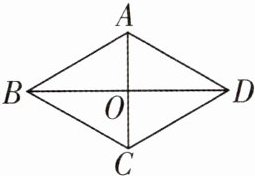
5 [2024 陕西咸阳秦都区调研]如图,□ABCD 的对角线 AC 与 BD 相交于点 O,添加

建议用时 20 分钟 答案 D3
下列条件不能证明□ABCD 是菱形的是 ( )

A.∠ABD= ∠ADB
B.AC⊥BD
C.AB= BC
D.AC= BD

答案： D 【解析】A
∵ $\angle ABD=\angle ADB$，
∴ $AB=AD$，
∴ $□ ABCD$ 是菱形，故选项 A 不符合题意 B
∵ 四边形 ABCD 是平行四边形，$AC\perp BD$，
∴ $□ ABCD$ 是菱形，故选项 B 不符合题意 C
∵ 四边形 ABCD 是平行四边形，$AB=BC$，
∴ $□ ABCD$ 是菱形，故选项 C 不符合题意 D 由四边形 ABCD 是平行四边形，$AC=BD$，不能证明 $□ ABCD$ 是菱形，故选项 D 符合题意

6 [2025 陕西咸阳期中]如图,在四边形 ABCD 中,对角线 AC 与 BD 相交于点 O,BD 垂直平分 AC,点 E 是 OB 上一点,且∠AEO= ∠CDO. 求证:四边形 AECD 是菱形.

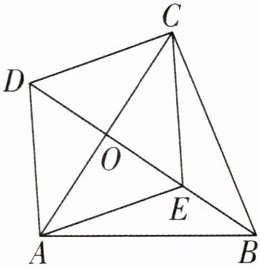
答案： 【证明】
∵ BD 垂直平分 AC，
∴ $OA=OC$, $\angle DOC=\angle DOA=\angle AOE=90^\circ$. 在 $\triangle AEO$ 与 $\triangle CDO$ 中，$\left\{\begin{array}{l} \angle AEO=\angle CDO,\\ \angle AOE=\angle COD,\\ OA=OC,\end{array}\right.$
∴ $\triangle AEO\cong \triangle CDO$（AAS），
∴ $CD=AE$.
∵ $\angle AEO=\angle CDO$，
∴ $CD// AE$，
∴ 四边形 AECD 是平行四边形.
∵ $AC\perp DE$，
∴ $□ AECD$ 是菱形.

7 [2025 河南郑州期中]如图,在△ABO 中,AO= BO,∠O= 120°,C 是 AB 的中点,若将△ABO 绕点 C 逆时针旋转 180°,则旋转前后两个三角形组成的图形是 ( )

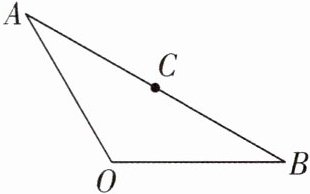
A.等腰梯形
B.菱形
C.正五边形
D.正三角形

答案： B 【解析】如图，由旋转可知 $AO'=BO$, $AO=BO'$.
∵ $AO=BO$，
∴ $AO'=BO=AO=BO'$，
∴ 四边形 AOBO' 为菱形，即旋转前后两个三角形组成的图形是菱形. 故选 B.

8 如图,在四边形 ABCD 中,AC 是 BD 的垂直平分线,E 是 CD 上一点,BE 交 AC 于 F,连接 DF,∠BEC= ∠ADF,试证明四边形 ABCD 是菱形.

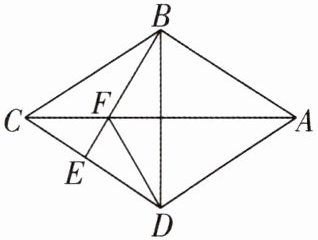
答案： 【证明】
∵ AC 是 BD 的垂直平分线，
∴ $AB=AD$, $BC=CD$，
∴ $\angle ABD=\angle ADB$, $\angle BAF=\angle DAF$. 在 $\triangle ABF$ 和 $\triangle ADF$ 中，$\left\{\begin{array}{l} AB=AD,\\ \angle BAF=\angle DAF,\\ AF=AF,\end{array}\right.$
∴ $\triangle ABF\cong \triangle ADF$（SAS），
∴ $\angle ABF=\angle ADF$.
∵ $\angle BEC=\angle ADF$，
∴ $\angle BEC=\angle ABF$，
∴ $AB// CD$，
∴ $\angle BAC=\angle ACD$. 又
∵ $\angle BAC=\angle DAC$，
∴ $\angle CAD=\angle ACD$，
∴ $AD=CD$.
∵ $AB=AD$, $BC=CD$，
∴ $AB=CB=CD=AD$，
∴ 四边形 ABCD 是菱形.