《2025年初中必刷题九年级数学上册北师大版》

1一个四边形顺次添加下列中的三个条件便得到正方形：
a.两组对边分别相等
b.一组对边平行且相等
c.一组邻边相等
d.一个角是直角
顺次添加的条件：①$a→c→d$,②$b→d→c$,③$a→b→c$,则正确的是( )


A.仅①
B.仅③
C.①②
D.②③

答案： C　[解析]①由a得到两组对边分别相等的四边形是平行四边形，添加c得一组邻边相等的平行四边形是菱形，再添加d得一个角是直角的菱形是正方形，故①正确;②由b得到一组对边平行且相等的四边形是平行四边形，添加d得有一个角是直角的平行四边形是矩形，再添加c得一组邻边相等的矩形是正方形，故②正确;③由a得到两组对边分别相等的四边形是平行四边形，添加b得到一组对边平行且相等的平行四边形仍是平行四边形，再添加c得一组邻边相等的平行四边形是菱形，不能得到四边形是正方形，故③不正确.故选C.

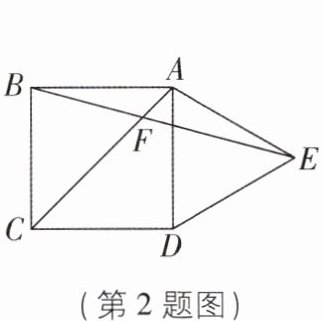
2[2024江西南昌调研]如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则$∠BFC$的度数为( )

A.$45^{\circ }$
B.$55^{\circ }$
C.$60^{\circ }$
D.$75^{\circ }$

答案： C　[解析]
∵四边形ABCD是正方形，
∴AB=AD.又
∵△ADE是等边三角形，
∴AE=AD=DE，∠DAE=60°，
∴AB=AE，
∴∠ABE=∠AEB，∠BAE=90°+60°=150°，
∴∠ABE=(180°−150°)÷2=15°.又
∵∠BAC=45°，
∴∠BFC=45°+15°=60°.故选C.

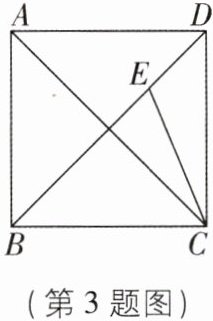
3[2025山东青岛校级期中]如图,正方形ABCD的边长为2,连接AC,BD,CE平分$∠ACD$交BD于点E,则DE的长是( )

A.$2-\sqrt {2}$
B.$2\sqrt {2}-1$
C.$\frac {2}{3}\sqrt {2}$
D.$2\sqrt {2}-2$

答案： D　[解析]如图,过点E作EF⊥DC于点F,设AC交BD于点O.
∵四边形ABCD是正方形，
∴AC⊥BD，∠BDC=45°.
∵CE平分∠ACD交BD于点E，
∴∠ECO=∠ECF，EO=EF.
∵正方形ABCD的边长为2，
∴AB=BC=2，
∴由勾股定理得AC=√(AB²+BC²)=√(2²+2²)=2√2，
∴CO=(1/2)AC=√2.在△EOC和△EFC中，{∠EOC=∠EFC，∠OCE=∠FCE，EO=EF}，
∴△EOC≌△EFC(AAS)，
∴CF=CO=√2.
∵EF⊥DC，∠BDC=45°，
∴△DEF为等腰直角三角形，
∴EF=DF=DC−CF=2−√2，
∴DE=√2DF=2√2−2.
故选D.

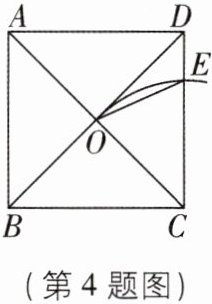
4[2025福建泉州质检]如图,在正方形ABCD中,对角线AC与BD相交于点O,以点C为圆心,CO长为半径作弧,交CD于点E,连接OE,则$∠DOE= $______度.

答案： 22.5　[解析]
∵四边形ABCD是正方形，
∴AC=BD，OC⊥OD，OA=OC，OB=OD，
∴OC=OD，∠COD=90°，
∴∠ODC=∠OCD=45°.由作图可知OC=CE，
∴∠COE=∠CEO=(180°-45°)/2=67.5°，
∴∠DOE=∠COD - ∠COE=90°-67.5°=22.5°.故答案为22.5.

5[2024陕西咸阳秦都区期中]如图,在平面直角坐标系中,正方形ABCD的顶点$A(-2,0)$,$B(0,1)$均在坐标轴上,则点C的坐标为______.

答案： (-1,3)　[解析]如图，过C作CH⊥y轴于H.
∵A的坐标是(-2,0)，B的坐标是(0,1)，
∴OA=2，OB=1.
∵四边形ABCD是正方形，
∴AB=BC，∠ABC=90°.
∵∠CBH+∠ABO+∠ABC=180°，
∴∠CBH+∠ABO=90°.
∵∠BAO+∠ABO=90°，
∴∠CBH=∠BAO.
∵∠BHC=∠AOB=90°，BC=AB，
∴△BCH≌△ABO(AAS)，
∴CH=OB=1，BH=AO=2，
∴OH=OB+BH=3，
∴C的坐标是(-1,3).故答案为(-1,3).

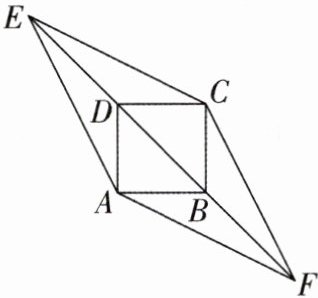
6[2025山西晋中质检]如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,使$BF= DE= \sqrt {2}$,连接AE,AF,CE,CF.
(1)求证：四边形AECF是菱形；
(2)求四边形AECF的面积.

答案：
(1)[证明]如图，连接AC，交BD于点O.
∵四边形ABCD是正方形，
∴BD⊥AC，BO=DO，AO=CO.
∵BF=DE，
∴OD+DE=OB+BF，即OE=OF，
∴四边形AECF是平行四边形.又
∵EF⊥AC，
∴四边形AECF是菱形.
(2)[解]
∵四边形ABCD是边长为1的正方形，
∴AB=AD=1，
∴BD=AC=√2.
∵BF=DE=√2，
∴EF=3√2，
∴四边形AECF的面积为(1/2)·AC·EF=(1/2)×√2×3√2=3.

7已知正方形ABCD,点E在边AB上,以CE为边作正方形CEFG,如图所示,连接DG.求证：$\triangle BCE\cong \triangle DCG$.王俊同学的证明过程如下,他的证明过程正确吗？若不正确,请改正.
证明：∵四边形ABCD和四边形CEFG都是正方形,∴$CB= CD$,$CE= CG$.∵$∠B= ∠CDG= 90^{\circ }$,∴$Rt\triangle BCE\cong Rt\triangle DCG(HL)$.

答案： [解]他的证明过程不正确，正确证明过程如下:
∵四边形ABCD和四边形CEFG都是正方形，
∴CB=CD，CE=CG，∠BCD=∠ECG=90°，
∴∠BCD - ∠ECD=∠ECG - ∠ECD，
∴∠BCE=∠GCD，
∴△BCE≌△DCG(SAS).