《2025年初中必刷题九年级数学上册北师大版》

1 新考法 [2024 河北唐山调研,中]将图(1)中两个三角形按图(2)所示的方式摆放,其中四边形 ABCD 为矩形,连接 PQ,MN,甲、乙两人有如下结论：
甲：若四边形 ABCD 是边长为 1 的正方形,则四边形 PQMN 必是正方形；
乙：若四边形 PQMN 为正方形,则四边形 ABCD 必是边长为 1 的正方形。下列判断正确的是( )

A.甲正确,乙不正确
B.甲不正确,乙正确
C.甲、乙都不正确
D.甲、乙都正确

答案： D 【解析】甲：
∵四边形 ABCD 是边长为 1 的正方形，
∴AB=BC=CD=AD=1，∠BAD=90°，
∴AQ=4 - 1=3，AP=3 + 1=4，∠PAQ=90°，
∴PQ²=AQ²+AP²=25，
∴PQ=5，同理可得 MN=5，
∴四边形 PQMN 是菱形. 在△QMD 和△PQA 中，MQ=QP，MD=QA，DQ=AP，
∴△QMD≌△PQA(SSS)，
∴∠MQD=∠APQ.
∵∠AQP+∠QPA=90°，
∴∠AQP+∠MQD=90°，
∴∠MQP=90°，则四边形 PQMN 必是正方形，
∴甲正确. 乙：若四边形 PQMN 为正方形，则 PQ=PN=MN=MQ=5，且∠QMD+∠MQD=∠AQP+∠MQD=∠AQP+∠APQ=90°，
∴∠MQD=∠APQ，∠QMD=∠AQP. 在△QMD 和△PQA 中，∠QMD=∠AQP，MQ=PQ，∠MQD=∠QPA，
∴△QMD≌△PQA(ASA)，
∴QD=AP=4，MD=AQ=3，同理可得 QD=AP=MC=BN=4. 又
∵BP=MD=AQ=3，
∴AB=AD=1. 又
∵四边形 ABCD 为矩形，
∴四边形 ABCD 必是边长为 1 的正方形，
∴乙正确. 故选 D.

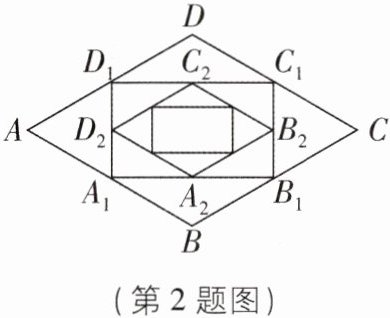
2 [2025 广东广州期中,中]如图,已知菱形 ABCD 的边长为 2,∠BAD = 60°,进行如下操作：第一次,顺次连接菱形 ABCD 各边的中点,得到四边形$ A_1B_1C_1D_1；$第二次,顺次连接四边形$ A_1B_1C_1D_1 $各边的中点,得到四边形$ A_2B_2C_2D_2；$…,如此反复操作下去,则第 n 次操作后,得到四边形 AₙBₙCₙDₙ 的面积是( )

A.$\frac{\sqrt{3}}{2^n}$
B.$\frac{\sqrt{3}}{2^{n - 1}}$
C.$\frac{\sqrt{3}}{2^{n + 1}}$
D.$\frac{\sqrt{3}}{2^{2n}}$

答案： B 【解析】连接 AC，BD，如图.
∵点 A₁，B₁ 分别是 AB 和 BC 的中点，点 C₁，D₁ 分别是 CD 和 AD 的中点，
∴A₁B₁ 是△ABC 的中位线，C₁D₁ 是△ACD 的中位线，
∴A₁B₁//AC，A₁B₁=$\frac{1}{2}$AC，C₁D₁//AC，C₁D₁=$\frac{1}{2}$AC，
∴A₁B₁//C₁D₁，A₁B₁=C₁D₁，
∴四边形 A₁B₁C₁D₁ 是平行四边形. 又
∵四边形 ABCD 是菱形，
∴AC⊥BD.
∵A₁，D₁ 分别是 AB，AD 的中点，
∴A₁D₁ 是△ABD 的中位线，
∴A₁D₁//DB，
∴A₁D₁⊥C₁D₁，
∴∠A₁D₁C₁=90°，
∴四边形 A₁B₁C₁D₁ 是矩形.
∵四边形 ABCD 是菱形，
∴AD=AB.
∵A₁D₁=$\frac{1}{2}$AD，A₁A=$\frac{1}{2}$AB，
∴A₁D₁=A₁A.
∵∠DAB=60°，
∴△D₁AA₁ 是等边三角形. 又
∵A₁A=$\frac{1}{2}$AB=1，
∴A₁D₁=A₁A=1. 易得 C₁D₁=$\sqrt{3}$，
∴四边形 A₁B₁C₁D₁ 的面积为$\sqrt{3}$；依次类推，四边形 A₂B₂C₂D₂ 的面积为$\frac{\sqrt{3}}{2}$；四边形 A₃B₃C₃D₃ 的面积为$\frac{\sqrt{3}}{2^{2}}$；…，
∴四边形 AₙBₙCₙDₙ 的面积为$\frac{\sqrt{3}}{2^{n - 1}}$. 故选 B.

3 [中]如图,已知四边形 ABCD 为正方形,AB = $2\sqrt{2}$,点 E 为对角线 AC 上一动点,连接 DE,过点 E 作 EF ⊥ DE,交 BC 延长线于点 F,以 DE,EF 为邻边作矩形 DEFG,连接 CG。有下列结论：
①矩形 DEFG 是正方形；②2CE + CG = $\sqrt{2}AD$；③CG 平分 ∠DCF；④CE = CF。其中正确的结论有( )

A.①③
B.②④
C.①②③
D.①②③④

答案： A 【解析】过 E 作 EM⊥BC 于 M 点，EN⊥CD 于 N 点，如图所示.
∵四边形 ABCD 是正方形，
∴∠BCD=90°，∠ECN=45°，
∴∠EMC=∠ENC=∠BCD=90°，
∴NE=NC，
∴四边形 EMCN 为正方形，
∴EM=EN.
∵四边形 DEFG 是矩形，
∴∠DEN+∠NEF=∠MEF+∠NEF=90°，
∴∠DEN=∠MEF. 在△DEN 和△FEM 中，∠DNE=∠FME=90°，EN=EM，∠DEN=∠FEM，
∴△DEN≌△FEM(ASA)，
∴ED=EF，
∴矩形 DEFG 为正方形，故①正确.
∴DE=DG.
∵四边形 ABCD 是正方形，
∴AD=DC，∠ADE+∠EDC=90°.
∵∠EDC+∠CDG=90°，
∴∠ADE=∠CDG. 在△ADE 和△CDG 中，AD=CD，∠ADE=∠CDG，DE=DG，
∴△ADE≌△CDG(SAS)，
∴AE=CG，∠DAE=∠DCG=45°.
∵∠DCF=90°，
∴CG 平分∠DCF，故③正确. AC=AE+CE=CE+CG=$\sqrt{2}$AD，故②错误. 当 DE⊥AC 时，点 C 与点 F 重合，
∴CE 不一定等于 CF，故④错误. 故选 A.

4 [2025 湖北武汉期末,较难]如图,点 A,B 分别是 x 轴和 y 轴上的动点,且 OA + OB = 6,取 AB 的中点 P,则所有满足条件的点 P 围成的封闭图形的面积为______。

答案： 18 【解析】设点 P 的坐标为(x,y).
∵P 是 AB 中点，A 在 x 轴上，B 在 y 轴上，
∴A(2x,0)B(0,2y)，
∴OA=|2x|=2|x|，OB=|2y|=2|y|.
∵OA+OB=6，
∴|x|+|y|=3. 如图，当 x≥0，y≥0 时，点 P 运动的轨迹是线段 CD，其中 OC=OD=3；当 x≥0，y≤0 时，点 P 运动的轨迹是线段 CF，其中 OC=OF=3；当 x≤0，y≥0 时，点 P 运动的轨迹是线段 DE，其中 OE=OD=3；当 x≤0，y≤0 时，点 P 运动的轨迹是线段 EF，其中 OE=OF=3.
∵EC⊥DF，OC=OD=OE=OF，
∴四边形 CDEF 是正方形，
∴所有满足条件的点 P 围成的封闭图形是正方形，
∴这个封闭图形的面积为$\frac{1}{2}$×6×6=18. 故答案为 18.

5 [2024 江苏扬州期中,较难]如图,在四边形 ABCD 中,∠A = ∠B = 90°,AB = BC = 4,AD = 3,E 是边 AB 上一点,且 ∠DCE = 45°,则 DE 的长度是______。

答案： 3.4 【解析】如图，过 C 作 CG⊥AD，交 AD 的延长线于 G，并延长 DG 至 F，使 GF=BE，连接 CF.
∵∠A=∠B=∠CGA=90°，AB=BC，
∴四边形 ABCG 为正方形，
∴AG=BC=4，∠BCG=90°，BC=CG.
∵AD=3，
∴DG=4 - 3=1.
∵BC=CG，∠B=∠CGF，BE=FG，
∴△EBC≌△FGC(SAS)，
∴CE=CF，∠ECB=∠FCG.
∵∠DCE=45°，
∴∠BCE+∠DCG=∠DCG+∠FCG=45°，
∴∠DCE=∠DCF.
∵CE=CF，∠DCE=∠DCF，DC=DC，
∴△ECD≌△FCD(SAS)，
∴ED=DF. 设 ED=x，则 EB=FG=x - 1，
∴AE=4-(x - 1)=5 - x.
∵在 Rt△AED 中，AE²+AD²=DE²，
∴(5 - x)²+3²=x²，解得 x=3.4，
∴DE=3.4. 故答案为 3.4.

6 核心素养 模型观念 [2024 福建福州质检,较难]如图(1),在平面直角坐标系中,放置一个边长为 5 的正方形 ABCD,使得它的两个顶点 B 和 A 恰好落在 x 轴正半轴和 y 轴正半轴上,M 为正方形的中心,连接 OM。
(1)若点 B 和点 A 分别在 x 轴和 y 轴的正半轴上滑动,求证：在这个运动过程中,M 始终在第一象限的角平分线上。
(2)如图(2),若点 A 运动到(0,3),求此时 M 点的坐标。

答案：
(1)【证明】作 ME⊥y 轴于 E 点，作 MF⊥x 轴于 F 点，如图
(1)所示，则四边形 EMFO 是矩形，∠EMF=∠MEA=∠MFB=90°，
∴∠EMA+∠AMF=90°.
∵四边形 ABCD 是正方形，
∴MA=MB，∠AMF+∠FMB=90°，
∴∠EMA=∠FMB. 在△MEA 和△MFB 中，∠MEA=∠MFB，∠EMA=∠FMB，MA=MB，
∴△MEA≌△MFB(AAS)，
∴ME=MF，
∴四边形 EMFO 是正方形，
∴点 M 在∠AOB 的平分线上，
∴M 始终在第一象限的角平分线上.
(2)【解】
∵点 A 运动到(0,3)，
∴OA=3.
∵AB=5，
∴OB=$\sqrt{AB^{2}-OA^{2}}$=$\sqrt{5^{2}-3^{2}}$=4. 作 ME⊥y 轴于 E 点，作 MF⊥x 轴于 F 点，作 CN⊥x 轴于 N 点，如图
(2)所示，则 MF//OA//CN，四边形 AONC 是直角梯形，四边形 EMFO 是正方形，∠AOB=∠CNB=90°.
∵四边形 ABCD 是正方形，
∴MA=MC，AB=BC，∠ABC=90°MF 是直角梯形 AONC 的中位线，∠ABO+∠CBN=90°.
∵∠BAO+∠ABO=90°，
∴∠BAO=∠CBN. 在△BAO 和△CBN 中，∠AOB=∠CNB，∠BAO=∠CBN，AB=BC，
∴△BAO≌△CBN(AAS)，
∴CN=OB=4，BN=OA=3，
∴MF=$\frac{1}{2}$(OA+CN)=$\frac{1}{2}$(3 + 4)=$\frac{7}{2}$OF=$\frac{1}{2}$(OB+BN)=$\frac{1}{2}$(4 + 3)=$\frac{7}{2}$，
∴M 点的坐标为($\frac{7}{2}$,$\frac{7}{2}$).