《2025年初中必刷题九年级数学上册北师大版》

1 [2025 黑龙江齐齐哈尔校级期末]从一张正方形铁皮上截去 2 cm 宽的一个长方形(长方形的长与正方形铁皮的边长相等),余下部分的面积是$ 48 cm^2,$则原来的正方形铁皮的面积是 ( )
$A. 24 cm^2$
$B. 32 cm^2$
$C. 8 cm^2$
$D. 64 cm^2$

答案： D 【解析】设原来正方形铁皮的边长为x cm，则余下部分为长x cm、宽(x - 2)cm的长方形。根据题意，得x(x - 2)=48，解得x = 8或x = - 6(不合题意，舍去)，
∴x² = 8×8 = 64。故选D。

2 [2025 陕西咸阳调研]用一根长 12 cm 的铁丝围成一个斜边长为 5 cm 的直角三角形,则这个直角三角形较短的直角边长为______ cm.

答案： 3 【解析】设一条直角边长为x cm，则另一条直角边长为(12 - 5 - x)cm。根据勾股定理，得x²+(12 - 5 - x)² = 5²，解得x₁ = 4，x₂ = 3，
∴两直角边长分别为3 cm和4 cm，
∴这个直角三角形较短的直角边长为3 cm。故答案为3。

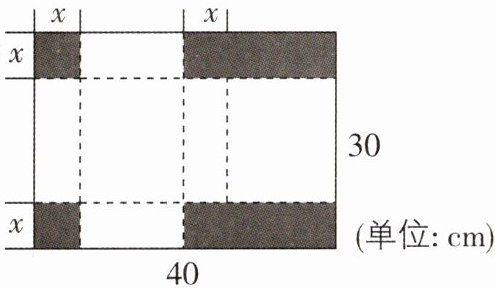
3 [2025 山东青岛校级质检]如图,把长 40 cm、宽 30 cm 的矩形纸板剪掉 2 个小正方形和 2 个小矩形(阴影部分即剪掉部分),将剩余的部分折成一个有盖的长方体盒子,设剪掉的小正方形的边长为 x cm(纸板的厚度忽略不计),若折成的长方体盒子的表面积是$ 950 cm^2,$则 x 的值是______.
]

答案： 5 【解析】依题意，得40×30 - 2x² - 2x·(40/2)=950，整理得x² + 20x - 125 = 0，解得x₁ = 5，x₂ = - 25(不合题意，舍去)，
∴x的值是5。故答案为5。

4 [2024 辽宁大连期中]一个两位数的个位数字与十位数字的和为 11,并且个位数字与十位数字的平方和为 85,则这个两位数是______.

答案：
92或29 【解析】

5 [2025 江西九江校级质检]如图是一张月历表,在此月历表上可以用一个矩形任意圈出 2×2 个位置上相邻的数(如 2,3,9,10). 如果圈出的 4 个数中最大数与最小数的积为 128,求这 4 个数中最小的数.
]

答案： 思路分析：第一步：审题——题图中圈出的4个数中，最大数与最小数的差是10 - 2 = 8；第二步：设未知数——设最小数为x，则最大数为x + 8；第三步：找等量关系列方程——最小数与最大数的乘积为128，即x(x + 8)=128。易错警示：由一元二次方程的根与系数的关系求出m的值后，容易忽略Δ≥0，导致错误。思路分析：题目所给月历表中，圈出的4个数中最大数与最小数的差始终是8，设最小数为x，则最大数为x + 8，列方程求解即可。
【解】设这4个数中最小数是x，则最大数为x + 8。根据题意，得x(x + 8)=128，解得x₁ = 8，x₂ = - 16(不合题意，舍去)，此时圈出的4个数为8，9，15，16。答：这4个数中最小的数是8。

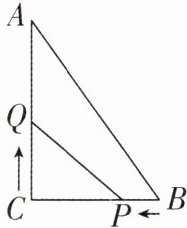
6 [2024 湖北武汉江岸区期中]如图,Rt△ACB 中,∠C= 90°,AC= 7,BC= 5,点 P 从点 B 出发向终点 C 以 1 个单位长度每秒的速度移动,点 Q 从点 C 出发向终点 A 以 2 个单位长度每秒的速度移动,P,Q 两点同时出发,一点先到达终点时 P,Q 两点同时停止移动,则当△PCQ 的面积等于 4 时,经过的时间为 ( )


A.1 秒
B.2 秒
C.4 秒
D.1 秒或 4 秒

答案： A 【解析】设经过t秒时，△PCQ的面积等于4。由题意得BP = t，CQ = 2t，则CP = 5 - t。
∵S△PCQ=(1/2)CQ·CP，
∴4=(1/2)×2t×(5 - t)，整理得t² - 5t + 4 = 0，解得t₁ = 1，t₂ = 4(不合题意，舍去)，即经过1秒时，△PCQ的面积等于4，故选A。

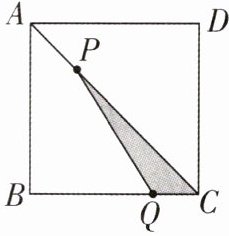
7 如图,在正方形 ABCD 中,AB= 5 cm,动点 P 以 √2 cm/s 的速度从点 A 出发,沿 AC 向点 C 移动,同时动点 Q 以 1 cm/s 的速度从点 C 出发,沿 CB 向点 B 移动,设 P,Q 两点移动时间为 t s(0＜t＜5). 在 P,Q 两点移动的过程中,PQ 的长度能否等于√10 cm? 若能,求出此时 t 的值;若不能,请说明理由.
]

答案： 思路分析：AC = 5√2，AP = √2t，PC = 5√2 - √2t，作PH⊥BC，PH = HC，PC = 5√2 - √2t，PH = 5 - t，CQ = t，HQ = |5 - 2t|，勾股定理，PQ = √10，求t值。
【解】能。在正方形ABCD中，
∵AB = 5 cm，
∴AC = 5√2 cm。由题意得AP = √2t cm，CQ = t cm，
∴PC=(5√2 - √2t)cm，BQ=(5 - t)cm。过点P作PH⊥BC于点H，则易得PH = HC=(5 - t)cm，
∴HQ = |HC - CQ| = |5 - 2t| cm．在Rt△PHQ中，
∵∠PHQ = 90°，
∴PH² + HQ² = PQ²。
∵PQ的长度等于√10 cm，
∴(5 - t)²+(5 - 2t)²=(√10)²解得t₁ = 2，t₂ = 4。故在P，Q两点移动的值为2或4。