《2025年初中必刷题九年级数学上册北师大版》

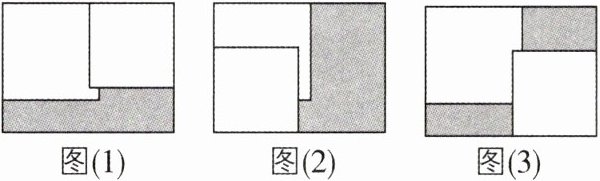
1 [2024 湖北随州调研,中]一张矩形纸片上放置两张边长分别为 3 cm 和 4 cm 的小正方形纸片. 按照图(1)放置时,矩形纸片没有被两张正方形纸片覆盖的部分(阴影部分)的面积为$ 8 cm^2;$按照图(2)放置时,矩形纸片没有被两张正方形纸片覆盖的部分的面积为$ 11 cm^2,$若把两张正方形纸片按图(3)放置,则矩形纸片没有被两张正方形纸片覆盖的部分的面积为 ( )
$A. 5 cm^2$
$B. 6 cm^2$
$C. 7 cm^2$
$D. 8 cm^2$
]

答案： C 【解析】设矩形纸片的长为x cm，宽为y cm。依题意，得{xy = 16 + 3(x - 4)+8，①；xy = 16 + 3(y - 4)+11，②。(② - ①)÷3，得y - x + 1 = 0，
∴x = y + 1。③ 将③代入②，得y(y + 1)=16 + 3(y - 4)+11，整理，得y² - 2y - 15 = 0，解得y₁ = 5，y₂ = - 3(舍去)，
∴x = 6。
∴按题图
(3)放置时，矩形纸片没有被两张正方形纸片覆盖的部分的面积为(x - 4)·(y - 3)+(x - 3)(y - 4)=2×2 + 3×1 = 7(cm²)。故选C。

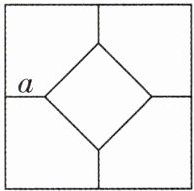
2 新考法 [2025 山东青岛期末,中]如图,一块正方形地砖的图案是由 4 个全等的五边形和 1 个小正方形组成的,已知小正方形的面积和五边形的面积相等,并且图中线段 a 的长度为√10 - 2,则这块地砖的面积为 ( )

A.50
B.40
C.30
D.20
]

答案：
B 【解析】如图，连接小正方形的两条对角线，设FH与EG交于点O。根据题意易知，点O为正方形ABCD，EFGH的中心，
∴S△EOF=(1/4)S正方形EFGH，即S正方形EFGH = 4S△EOF。
∵S五边形AMFEP = S正方形EFGH，
∴S五边形AMFEP = 4S△EOF。
∵S五边形AMFEP=(1/4)S正方形ABCD - S△EOF，
∴(1/4)S正方形ABCD = 5S△EOF。设正方形ABCD的边长为2x，则OF = OE = x - a，
∴(1/4)·2x·2x = 5×(1/2)(x - a)²，解得x=(5±√10)a/3。
∵a = √10 - 2，
∴x = √10或(7√10 - 20)/3。
∵(7√10 - 20)/3 ＜ a = √10 - 2，
∴x = √10，
∴S正方形ABCD = 2√10×2√10 = 40。故选B。

3 [中]如图,将图(1)的正方形纸片剪成四块,再用这四块小纸片进行拼接,恰好拼成一个如图(2)无缝隙、不重叠的矩形,则 $\frac{b}{a}$ = ______.
]

答案： (1 + √5)/2 【解析】题图
(1)的面积为(a + b)² = a² + 2ab + b²，题图
(2)的面积为b(a + 2b)=ab + 2b²，
∴a² + 2ab + b² = ab + 2b²，
∴b² - ab - a² = 0，
∴(b/a)²-(b/a)-1 = 0，
∴b/a=(1±√5)/2。
∵b/a ＞ 0，
∴b/a=(1 + √5)/2。

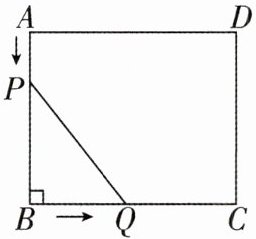
4 [2024 广东河源期中,中]如图,在长方形 ABCD 中,AB= 5 cm,BC= 6 cm,点 P 从点 A 开始沿边 AB 向终点 B 以 1 cm/s 的速度运动,与此同时,点 Q 从点 B 开始沿边 BC 向终点 C 以 2 cm/s 的速度运动. 如果 P,Q 分别从 A,B 同时出发,当点 Q 运动到点 C 时,两点同时停止运动. 设运动时间为 t s.
(1)当 t 为何值时,PQ 的长度等于 5 cm?
(2)是否存在 t 的值,使得五边形 APQCD 的面积等于$ 26 cm^2? $若存在,请求出此时 t 的值;若不存在,请说明理由.
]

答案： 【解】
(1)
∵P从点A开始沿边AB向终点B以1 cm/s的速度运动，
∴AP = t cm。
∵AB = 5 cm，
∴PB=(5 - t)cm。
∵点Q从点B开始沿边BC向终点C以2 cm/s的速度运动，
∴BQ = 2t cm，由题意得(5 - t)²+(2t)² = 5²，解得t₁ = 0，t₂ = 2。
∴当t = 0或2时，PQ的长度等于5 cm。
(2)存在t = 1，使得五边形APQCD的面积等于26 cm²。理由如下：
∵长方形ABCD的面积是5×6 = 30(cm²)，五边形APQCD的面积等于26 cm²，
∴△PBQ的面积为30 - 26 = 4(cm²)，
∴(5 - t)×2t×(1/2)=4，解得t₁ = 4(不合题意，舍去)，t₂ = 1。即当t = 1时，使得五边形APQCD的面积等于26 cm²。

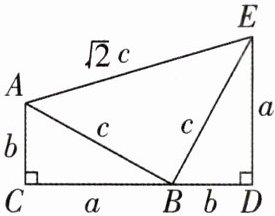
5 核心素养 几何直观 [2024 安徽淮北质检,较难]如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a,b,c 是 Rt△ABC 和 Rt△BED 的边长,易知 AE= √2 c,这时我们把关于 x 的形如 $ax^2 + \sqrt{2}cx + b = 0$ 的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程” $ax^2 + \sqrt{2}cx + b = 0$ 必有实数根;
(3)若 x = -1 是“勾系一元二次方程” $ax^2 + \sqrt{2}cx + b = 0$ 的一个根,且四边形 ACDE 的周长是 $6\sqrt{2}$,求△ABC 的面积.
]

答案：
(1)【解】当a = 3，b = 4，c = 5时，“勾系一元二次方程”为3x² + 5√2x + 4 = 0。(答案不唯一)
(2)【证明】根据题意，得Δ=(√2c)² - 4ab = 2c² - 4ab。
∵a² + b² = c²，
∴2c² - 4ab = 2(a² + b²)-4ab = 2(a - b)²≥0，即Δ≥0，
∴“勾系一元二次方程”ax² + √2cx + b = 0必有实数根。
刷有所得：当销售问题中出现“要使顾客尽量得到实惠”或“最大限度减少库存”等实际要求时，要根据要求对所求得的解进行取舍。思路分析：
(2)根据题意可得△PBQ的面积，再根据三角形的面积公式代入相应线段的长即可得到方程，再解方程即可。
(3)【解】当x = - 1时，有a - √2c + b = 0，即a + b = √2c。
∵2a + 2b + √2c = 6√2，即2(a + b)+√2c = 6√2，
∴3√2c = 6√2，
∴c = 2，
∴a² + b² = c² = 4，a + b = 2√2。
∵(a + b)² = a² + b² + 2ab，
∴ab = 2，
∴S△ABC=(1/2)ab = 1。