《2025年初中必刷题九年级数学上册北师大版》

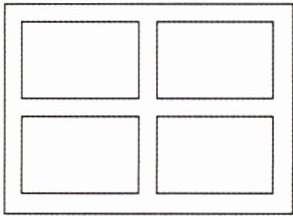
1[2025河南洛阳期末,中]如图,某项绿化工程中有一块长为60米,宽为40米的矩形空地,计划在其中修建四块相同的矩形绿地,四块绿地之间及周边都留有人行通道.
(1)原计划要求四块相同的矩形绿地面积之和为1836平方米,且四块绿地之间及周边留有宽度相等的人行通道,则人行通道的宽度是多少米?(参考数据:$\sqrt {7744}= 88$)
(2)实际绿化时修改方案为①保证横向人行通道与原计划设计的宽度一样;②四块相同的矩形绿地的长、宽之比与整个空地的长、宽之比相等;③三条纵向人行通道宽度相等.请你设计一种纵向人行通道的宽度,使之恰能满足上述方案.

答案： 1.【解】
(1)设人行通道的宽度是x米.由题意得(60-3x)(40-3x)=1836,整理得3x²-100x+188=0.
∵Δ=(-100)²-4×3×188=7744＞0,
∴x=(100±88)/6,
∴x₁=2,x₂=94/3(舍去).答:人行通道的宽度是2米.
(2)设纵向人行通道的宽度是y米,则每块矩形绿地的长为(60-3y)/2米,即为(30-1.5y)米,宽为(40-2×3)/2米,即为17米.由题意得(30-1.5y)/17=60/40,解得y=3.答:纵向人行通道的宽度为3米时,恰能满足上述方案.

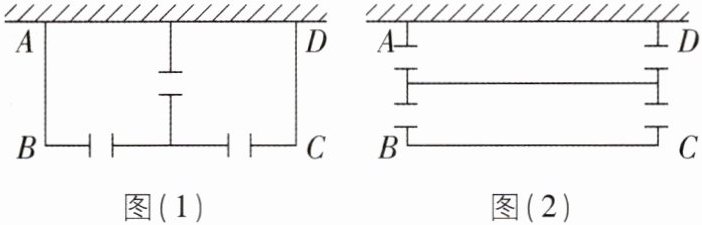
2[2025黑龙江牡丹江调研,中]某农场用篱笆围成饲养室,一面靠现有墙(墙长为15m),现有两种方案供选择(如图):
方案1:围成一个矩形,中间用垂直于墙的篱笆隔开,并留三扇1m宽的门,如图(1)所示;
方案2:围成一个矩形,中间用平行于墙的篱笆隔开,并留四扇1m宽的门,如图(2)所示.
已知计划中的篱笆(不包括门)总长为24m(全部用完),请根据题意解答下列问题:
(1)若方案1中矩形ABCD的面积为$54m^{2}$,求AB的长;
(2)方案2中矩形ABCD的面积能为$54m^{2}$吗?若能,请求出AB的长;若不能,说明理由.

答案： 2.【解】
(1)设方案1中AB的长为x米,则BC的长为(24+3-3x)米.依题意,得x(24+3-3x)=54,整理得x²-9x+18=0,解得x₁=3,x₂=6.
∵0＜24+3-3x≤15,
∴4≤x＜9,
∴x₁=3不合题意,舍去,
∴x=6,
∴AB=6米.答:AB的长为6米.
(2)不能,理由如下:设方案2中AB的长为x米,则BC的长为1/2(24+4-2x)米.依题意,得1/2x(24+4-2x)=54,整理得x²-14x+54=0.
∵Δ=(-14)²-4×1×54=-20＜0,
∴该方程无实数解,
∴方案2中矩形ABCD的面积不能为54m².

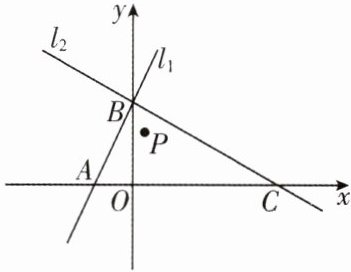
3[2025河北石家庄调研,中]如图,点$P(a,a+2)$是平面直角坐标系xOy中的一个动点,直线$l_{1}$与x轴,y轴分别交于点$A(-\frac {5}{2},0),B(0,5)$,直线$l_{2}$经过点B和点$(6,2)$并与x轴交于点C.
(1)求直线$l_{1}和l_{2}$的表达式及点C的坐标.
(2)当点P在$\triangle ABC$的内部(包含边界)时,
①求a的取值范围;
②是否存在点P,使得$∠OPA= 90^{\circ }$?若存在,直接写出点P的坐标;若不存在,请说明理由.

答案： 3.【解】
(1)设直线l₁的表达式为y=kx+b.把A(-5/2,0),B(0,5)代入,得{-5/2k+b=0,b=5,解得{k=2,b=5,
∴直线l₁的表达式为y=2x+5.设直线l₂的表达式为y=k₁x+b₁.把点B(0,5)和点(6,2)代入,得{b₁=5,6k₁+b₁=2,解得{k₁=-1/2,b₁=5,
∴直线l₂的表达式为y=-1/2x+5.令y=0,得-1/2x+5=0,解得x=10,
∴点C的坐标为(10,0).
(2)①
∵P(a,a+2),
∴点P在直线y=x+2上.令y=0,则x=-2,
∴直线y=x+2与x轴的交点为(-2,0).联立方程组{y=-1/2x+5,y=x+2,解得{x=2,y=4,
∴直线y=x+2与直线l₂的交点为点(2,4).
∵点P在△ABC的内部,
∴-2≤a≤2.②存在点P,使得∠OPA=90°,点P的坐标为((-13+√41)/8,(3+√41)/8).理由如下:
∵A(-5/2,0),
∴OA=5/2.设OA的中点为M,则M(-5/4,0).
∵∠OPA=90°,
∴PM=1/2OA,
∴√((a+5/4)²+(a+2)²)=1/2×5/2,解得a=(-13-√41)/8(不符合题意,舍去)或a=(-13+√41)/8,
∴P((-13+√41)/8,(3+√41)/8).