《2025年初中必刷题九年级数学上册北师大版》

1 [2024黑龙江哈尔滨中考]如图,在四边形ABCD中,AD//BC,点E在AB上,EF//AD交CD于点F,若AE：BE= 1：2,DF= 3,则FC的长为( )

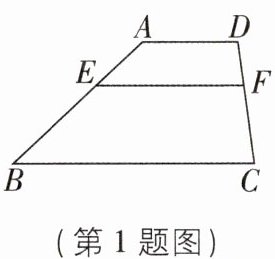
A.6
B.3
C.5
D.9

答案： A【解析】
∵在四边形ABCD中，AD//BC，EF//AD，
∴AD//EF//BC，
∴$\frac{AE}{EB}=\frac{DF}{FC}$，即$\frac{1}{2}=\frac{3}{FC}$，解得FC=6，故选A.

2 [2024陕西中考]如图,正方形CEFG的顶点G在正方形ABCD的边CD上,AF与DC交于点H,若AB= 6,CE= 2,则DH的长为( )

A.2
B.3
C.5/2
D.8/3

答案： B【解析】在正方形ABCD中，AB=6，
∴AB=AD=CD=6.在正方形CEFG中，CE=2，
∴CE=GF=CG=2，
∴DG=CD - CG=4.由题意得AD//BE，GF//BE，
∴AD//GF，
∴易得△ADH∽△FGH，$\frac{AD}{GF}=\frac{DH}{GH}$，即$\frac{6}{2}=\frac{DH}{4 - DH}$，解得DH=3，故选B.

3 [2024山东德州中考]如图,Rt△ABC中,∠ABC= 90°,BD⊥AC,垂足为D,AE平分∠BAC,分别交BD,BC于点F,E.若AB：BC= 3：4,则BF：FD为( )

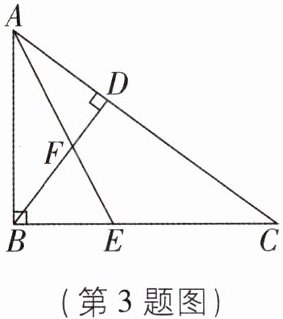
A.5：3
B.5：4
C.4：3
D.2：1

答案： A【解析】
∵AB∶BC=3∶4，
∴可设AB=3x，BC=4x.
∵∠ABC=90°，
∴AC=$\sqrt{AB^2+BC^2}$=5x，∠ABD+∠CBD=90°.
∵BD⊥AC，
∴∠ADB=∠BDC=∠ABC=90°，
∴∠CBD+∠C=90°，
∴∠C=∠ABD，
∴△ACB∽△ABD，
∴$\frac{AB}{AD}=\frac{AC}{AB}=\frac{5x}{3x}=\frac{5}{3}$.
∵AE平分∠BAC，
∴点F到AB，AC的距离相等.又
∵点A到BF，DF的距离相等，
∴$\frac{S_{\triangle ABF}}{S_{\triangle ADF}}=\frac{BF}{FD}=\frac{AB}{AD}=\frac{5}{3}$，即BF∶FD=5∶3，故选A.

4 [2024四川眉山中考]如图,菱形ABCD的边长为6,∠BAD= 120°,过点D作DE⊥BC,交BC的延长线于点E,连接AE分别交BD,CD于点F,G,则FG的长为______.

答案： $\frac{4\sqrt{7}}{5}$【解析】
∵菱形ABCD的边长为6，∠BAD=120°，
∴AD=BC=CD=6，AD//BC，∠BCD=120°，
∴∠DCE=60°.
∵DE⊥BC交BC的延长线于点E，
∴∠DEC=90°，
∴∠CDE=90° - ∠DCE=30°，
∴CE=$\frac{1}{2}$CD=3，
∴DE=3$\sqrt{3}$，BE=BC+CE=9.
∵AD//BE，
∴∠ADE=180° - ∠DEC=90°.在Rt△ADE中，AE=$\sqrt{DE^2+AD^2}=\sqrt{(3\sqrt{3})^2+6^2}=3\sqrt{7}$.
∵AD//BE，
∴易得△AFD∽△EFB，
∴$\frac{AF}{FE}=\frac{AD}{BE}=\frac{6}{9}=\frac{2}{3}$，
∴AF=$\frac{2}{5}$AE=$\frac{2}{5}×3\sqrt{7}=\frac{6\sqrt{7}}{5}$.
∵AD//CE，
∴△AGD∽△EGC，
∴$\frac{AG}{EG}=\frac{AD}{CE}=\frac{6}{3}=2$，
∴AG=$\frac{2}{3}$AE=$\frac{2}{3}×3\sqrt{7}=2\sqrt{7}$，
∴FG=AG - AF=2$\sqrt{7}$-$\frac{6\sqrt{7}}{5}=\frac{4\sqrt{7}}{5}$.故答案为$\frac{4\sqrt{7}}{5}$.

5 [2024上海中考]如图所示,在矩形ABCD中,E为边CD上一点,且AE⊥BD.
(1)求证：$AD^2= DE·DC；$
(2)F为线段AE延长线上一点,且满足EF= CF= 1/2BD,求证：CE= AD.

答案：
【证明】（1）
∵四边形ABCD是矩形，
∴∠BAD=∠ADE=90°，AB=DC，
∴∠ABD+∠ADB=90°.
∵AE⊥BD，
∴∠DAE+∠ADB=90°，
∴∠ABD=∠DAE.
∵∠BAD=∠ADE=90°，
∴△ADE∽△BAD，
∴$\frac{AD}{BA}=\frac{DE}{AD}$，
∴AD²=DE·BA.
∵AB=DC，
∴AD²=DE·DC.
（2）如图，连接AC交BD于点O.
∵四边形ABCD是矩形，
∴∠ADE=90°，
∴∠DAE+∠AED=90°.
∵AE⊥BD，
∴∠DAE+∠ADB=90°，
∴∠ADB=∠AED.
∵∠FEC=∠AED，
∴∠ADB=∠FEC.
∵四边形ABCD是矩形，
∴OA=OD=$\frac{1}{2}$BD，
∴∠ADO=∠OAD.又
∵EF=CF=$\frac{1}{2}$BD，
∴OA=OD=EF=CF，∠FEC=∠FCE.
∵∠ADO=∠FEC，
∴∠ADO=∠OAD=∠FEC=∠FCE.在△ODA和△FEC中，$\begin{cases}\angle ODA=\angle FEC,\\\angle OAD=\angle FCE,\\OD=FE,\end{cases}$
∴△ODA≌△FEC(AAS)，
∴CE=AD.

6 [2024江苏镇江中考]如图,小杰从灯杆AB的底部点B处沿水平直线前进到达点C处,他在灯光下的影长CD= 3米,然后他转身按原路返回到点B处,返回过程中小杰在灯光下的影长可以是( )

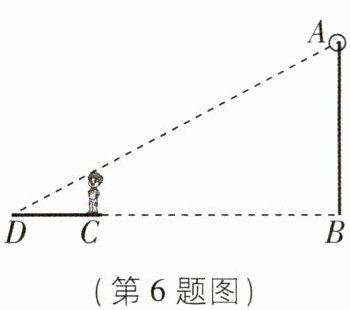
A.4.5米
B.4米
C.3.5米
D.2.5米

答案：
D【解析】如图，设返回过程中小杰身高为FH，连接AF并延长交BD于G.由FH//AB//EC，易得△FGH∽△AGB，△EDC∽△ADB，
∴易得$\frac{GH}{GB}=\frac{FH}{AB}=\frac{EC}{AB}=\frac{DC}{DB}$.由GB＜DB，得GH＜DC=3米.故选D.

7 [2024黑龙江绥化中考]如图,矩形OABC各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比1/3缩小,则顶点B在第一象限对应点的坐标是( )

A.(9,4)
B.(4,9)
C.(1,3/2)
D.(1,2/3)

答案： D【解析】
∵以原点O为位似中心，将矩形OABC按相似比$\frac{1}{3}$缩小，点B的坐标为(3,2)，
∴顶点B在第一象限对应点的坐标为$(3×\frac{1}{3},2×\frac{1}{3})$，即$(1,\frac{2}{3})$，故选D.