《2025年初中必刷题九年级数学上册北师大版》

1 [2025吉林长春质检,中]在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,用直尺和圆规在$AB上确定一点D$,使$\triangle ACD \backsim \triangle CBD$,根据作图痕迹判断,正确的是( )

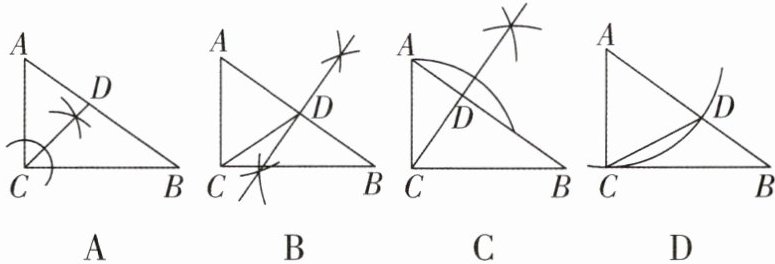
A.
B.
C.
D.

答案： C 【解析】当CD是AB的垂线时，△ACD∽△CBD。
∵CD⊥AB，
∴∠CDA=∠BDC=90°。
∵∠ACB=90°，
∴∠A+∠ACD=∠ACD+∠BCD=90°，
∴∠A=∠BCD，
∴△ACD∽△CBD。根据作图痕迹可知，C选项中，CD是AB的垂线，符合题意。故选C。

2 新考法[2024河北唐山期中,中]有一题目：“如图,在四边形$ABCD$中,$AB // CD$,$\angle B = \angle C = 90^{\circ}$,$AB = 2$,$BC = 7$,$CD = 6$. 当$\triangle ABP与\triangle PCD$相似时,求$BP$的长.”嘉嘉的结果为$BP = 3$或4. 而淇淇说：“嘉嘉考虑的不周全,$BP$还应有另一个不同的值.”下列判断正确的是( )

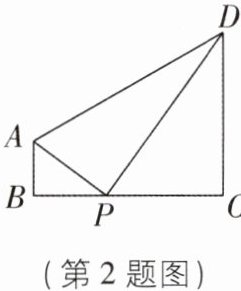
A.淇淇说得对,且$BP的另一个值是\frac{7}{4}$
B.淇淇说得不对,$BP$就等于3或4
C.嘉嘉求的结果不对,$BP$应等于3或5
D.两人都不对,$BP$应有4个不同值

答案： A 【解析】设BP=x，则CP=7-x。当∠APB=∠PDC时，
∵∠B=∠C=90°，
∴△APB∽△PDC，
∴$\frac{BP}{CD}=\frac{AB}{CP}$，
∴BP·CP=AB·CD=2×6=12，
∴x(7 - x)=12，解得x=3或x=4，
∴BP=3或4；当∠APB=∠DPC时，
∵∠B=∠C=90°，
∴△APB∽△DPC，
∴$\frac{BP}{CP}=\frac{AB}{CD}=\frac{2}{6}=\frac{1}{3}$，
∴3BP=CP，
∴3x=7 - x，解得$x=\frac{7}{4}$。综上所述，BP=3或4或$\frac{7}{4}$，故选A。

3 [2023广东中考,中]边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为______.

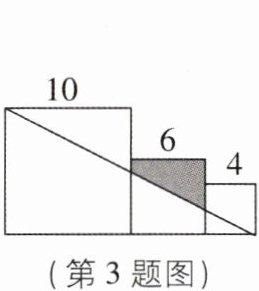
答案：
15 【解析】如图,由题意可知AD=DC=10,CG=CE=GF=6,∠CEF=∠EFG=90°,GH=4,
∴CH=10=AD.
∵∠D=∠DCH=90°,∠AJD=∠HJC,
∴△ADJ≌△HCJ,
∴CJ=DJ=5,
∴EJ=6 - 5=1.
∵GI//CJ,
∴∠GIH=∠CJH,∠IGH=∠JCH,
∴△HGI∽△HCJ,
∴$\frac{GI}{CJ}=\frac{GH}{CH}=\frac{2}{5}$
∴GI=2,
∴FI=4,
∴$S_{阴影}=\frac{1}{2}×(1 + 4)×6=15$。故答案为15。

4 [中]如图,在矩形$ABCD$中,$AB = 3$,$BC = 4$,点$P为射线BC$上的一个动点,过点$P的直线PQ垂直于AP与直线CD相交于点Q$,当$BP = 5$时,$CQ = $______.

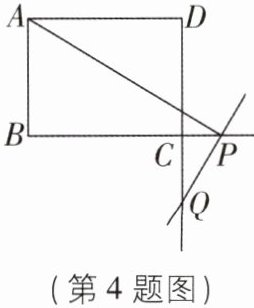
答案： $\frac{5}{3}$ 【解析】
∵BP=5，BC=4，
∴CP=1。
∵PQ⊥AP，
∴∠APQ=90°=∠ABC，
∴∠APB+∠BAP=90°=∠APB+∠BPQ，
∴∠BAP=∠BPQ。又
∵∠ABP=∠PCQ=90°，
∴△ABP∽△PCQ，
∴$\frac{AB}{CP}=\frac{BP}{CQ}$，
∴$\frac{3}{1}=\frac{5}{CQ}$，
∴$CQ=\frac{5}{3}$，故答案为$\frac{5}{3}$。

5 [较难]如图,在三角形纸板$ABC$中,$AC = 4$,$BC = 2$,$AB = 5$,$P是AC$上一点,过点$P沿直线剪下一个与\triangle ABC$相似的小三角形纸板,如果有4种不同的剪法,那么$AP$长的取值范围是______.

答案：
3≤AP＜4 【解析】如图
(1)所示，过P作PD//AB交BC于D，PE//BC交AB于E，则易知△PCD∽△ACB，△APE∽△ACB，此时0＜AP＜4。 如图
(2)所示，过P作∠APF=∠B交AB于F，则△APF∽△ABC，此时0＜AP≤4。 如图
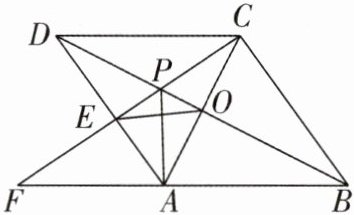
(3)所示，过P作∠CPG=∠CBA交BC于G，则△CPG∽△CBA，此时3≤AP＜4。 综上所述，要有4种不同的剪法，则AP长的取值范围是3≤AP＜4。

6 [2024山东枣庄期末,中]如图,点$P是菱形ABCD的对角线BD$上一点,连接$CP$并延长,交$AD于E$,交$BA的延长线于点F$,连接$AC交BD于O$,连接$OE$,$AP$.
(1)求证：$PE \cdot PF = PC^{2}$.
(2)若$CE \perp BC$,求证：$\triangle POC \backsim \triangle AEC$.

答案： 【证明】
(1)
∵四边形ABCD是菱形，
∴AD=CD，∠CDP=∠ADP，CD//AB。在△CDP和△ADP中，$\begin{cases}CD = AD\\∠CDP = ∠ADP\\DP = DP\end{cases}$，
∴△CDP≌△ADP(SAS)，
∴PC=PA，∠DCP=∠DAP。
∵CD//AB，
∴∠DCP=∠F，
∴∠DAP=∠F。
∵∠APE=∠FPA，
∴△PAE∽△PFA，
∴$\frac{PA}{PF}=\frac{PE}{AP}$，
∴$PA^2=PE\cdot PF$，
∴$PE\cdot PF=PC^2$。
(2)
∵CE⊥BC，
∴∠ECB=90°。
∵AD//BC，
∴∠CEA=90°。
∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠COP=90°，
∴∠COP=∠CEA。
∵∠OCP=∠ECA，
∴△POC∽△AEC。

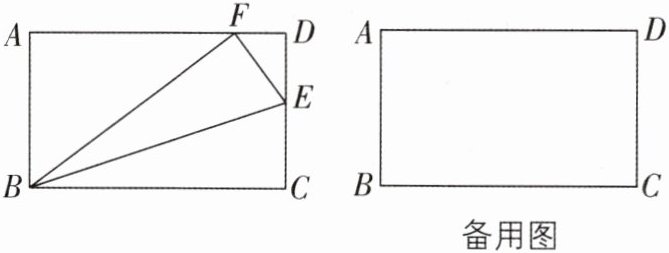
7 核心素养几何直观[2024江苏南通崇川区期末,难]矩形$ABCD$中,$AB ＜ BC$,$AB = 6$,$E是射线CD$上一点,点$C关于BE的对称点F恰好落在射线DA$上,连接$BF$,$EF$.
(1)如图,点$E在边CD$上,当$BC = 10$时,$DF$的长为______；当$AF \cdot DF = 9$时,$DF$的长为______.
(2)作$\angle ABF的平分线交射线DA于点M$,当$\frac{MF}{BC} = \frac{1}{2}$时,求$DF$的长.

答案：

(1)2 $3\sqrt{2}$ 【解析】当点E在边CD上，BC=10时，
∵点C关于BE的对称点F恰好落在射线DA上，
∴BF=BC=10，
∴$AF=\sqrt{BF^2 - AB^2}=\sqrt{10^2 - 6^2}=8$，
∴DF=AD - AF=10 - 8=2。当AF·DF=9时，
∵四边形ABCD是矩形，
∴∠A=∠D=90°。易知∠BFE=90°，
∴∠AFB+∠DFE=90°。
∵∠DEF+∠DFE=90°，
∴∠AFB=∠DEF，
∴△FAB∽△EDF，
∴$\frac{AF}{DE}=\frac{AB}{DF}$，
∴AF·DF=AB·DE。
∵AF·DF=9，AB=6，
∴$DE=\frac{3}{2}$，
∴$CE=CD - DE=\frac{9}{2}$。
∵点C关于BE的对称点F恰好落在射线DA上，
∴$EF=CE=\frac{9}{2}$，
∴$DF=\sqrt{EF^2 - DE^2}=3\sqrt{2}$。
(2)【解】①点F在AD边上时，过点M作MN⊥BF于点N，如图
(1)。
∵BM平分∠ABF，MA⊥AB，MN⊥BF，
∴MA=MN。
∵∠A=∠MNF=90°，∠AFB=∠NFM，
∴△FAB∽△FNM，
∴$\frac{MN}{AB}=\frac{MF}{BF}$。
∵$\frac{MF}{BC}=\frac{1}{2}$，BF=BC，
∴$\frac{NM}{AB}=\frac{MF}{BF}=\frac{1}{2}$。
∵AB=6，
∴MN=3=AM。在Rt△ABM和Rt△NBM中，$\begin{cases}BM = BM\\AM = MN\end{cases}$，
∴Rt△ABM≌Rt△NBM(HL)，
∴BN=AB=6。设MF=x，则BF=BC=2x，
∴FN=2x - 6。在Rt△MNF中，
∵$MN^2+FN^2=MF^2$，
∴$3^2+(2x - 6)^2=x^2$，解得x=5或x=3(舍去)，
∴BC=2x=10，
∴AD=BC=10，
∴DF=AD - AM - MF=2。 ②点F在边DA的延长线上时，过点M作MN⊥BF于点N，如图
(2)。同①可得AM=MN=3，BC=AD=10，MF=5，
∴DF=AD + AM + MF=18。综上所述，当$\frac{MF}{BC}=\frac{1}{2}$时，DF的长为2或18。