第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
5[2025陕西咸阳期中,中]如图,在正方形ABCD中,点M是对角线BD上的一点,连接AM,过点M作MN⊥AM,交CD于点N,以AM,MN为邻边作矩形AMNP.
(1)求证:矩形AMNP是正方形.
(2)若点N为CD的中点,且AD= 8,求正方形AMNP的面积.

(1)求证:矩形AMNP是正方形.
(2)若点N为CD的中点,且AD= 8,求正方形AMNP的面积.

答案:
(1)【证明】如图,过点M作ME⊥AD于点E,MF⊥CD于点F。
∵四边形ABCD是正方形,
∴∠ADC = 90°,∠MDA = ∠MDC = 45°。
∵ME⊥AD,MF⊥CD,
∴ME = MF。
∵∠MED = ∠MFD = ∠EDF = 90°,
∴四边形EMFD是正方形,
∴∠EMF = 90° = ∠AMN,
∴∠AME = ∠NMF。
在△AME和△NMF中,$\left\{\begin{array}{l} ∠AME = ∠NMF\\ ME = MF\\ ∠AEM = ∠NFM\end{array}\right.$,
∴△AME≌△NMF(ASA),
∴AM = NM。
又
∵四边形AMNP是矩形,
∴四边形AMNP是正方形。

(2)【解】连接AN。
∵在正方形ABCD中,点N为CD的中点,且AD = 8,
∴$DN=\frac{1}{2}CD=\frac{1}{2}AD = 4$,
∴在Rt△ADN中,$AN=\sqrt{AD^{2}+DN^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$。
∵四边形AMNP是正方形,
∴易知正方形AMNP的面积为$\frac{1}{2}AN^{2}=\frac{1}{2}×(4\sqrt{5})^{2}=40$。
(1)【证明】如图,过点M作ME⊥AD于点E,MF⊥CD于点F。
∵四边形ABCD是正方形,
∴∠ADC = 90°,∠MDA = ∠MDC = 45°。
∵ME⊥AD,MF⊥CD,
∴ME = MF。
∵∠MED = ∠MFD = ∠EDF = 90°,
∴四边形EMFD是正方形,
∴∠EMF = 90° = ∠AMN,
∴∠AME = ∠NMF。
在△AME和△NMF中,$\left\{\begin{array}{l} ∠AME = ∠NMF\\ ME = MF\\ ∠AEM = ∠NFM\end{array}\right.$,
∴△AME≌△NMF(ASA),
∴AM = NM。
又
∵四边形AMNP是矩形,
∴四边形AMNP是正方形。

(2)【解】连接AN。
∵在正方形ABCD中,点N为CD的中点,且AD = 8,
∴$DN=\frac{1}{2}CD=\frac{1}{2}AD = 4$,
∴在Rt△ADN中,$AN=\sqrt{AD^{2}+DN^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$。
∵四边形AMNP是正方形,
∴易知正方形AMNP的面积为$\frac{1}{2}AN^{2}=\frac{1}{2}×(4\sqrt{5})^{2}=40$。
6[2025广东韶关期中,中]【阅读理解】半角模型是指有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等.通过旋转或截长补短,将角的倍分关系转化为角的相等关系,并进一步构成全等三角形,用以解决线段关系、角度、面积等问题.
【初步探究】如图(1),在正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF.若∠EAF= 45°,将△ADF绕点A顺时针旋转90°,得到△ABG.易证:△AEF≌△AEG.
(1)根据以上信息填空:
①∠EAG= ____°;
②线段BE,EF,DF之间满足的数量关系为____.
【迁移探究】
(2)如图(2),在正方形ABCD中,若点E在CB的延长线上,点F在DC的延长线上,∠EAF= 45°,猜想线段BE,EF,DF之间的数量关系,并证明.
【拓展探索】
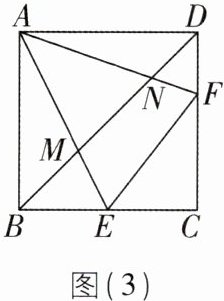
(3)如图(3),已知正方形ABCD的边长为$3\sqrt {2}$,E,F分别在BC,CD上,∠EAF= 45°,连接BD分别交AE,AF于点M,N,若点M恰好为线段BD的三等分点,且BM<DM,求线段MN的长.
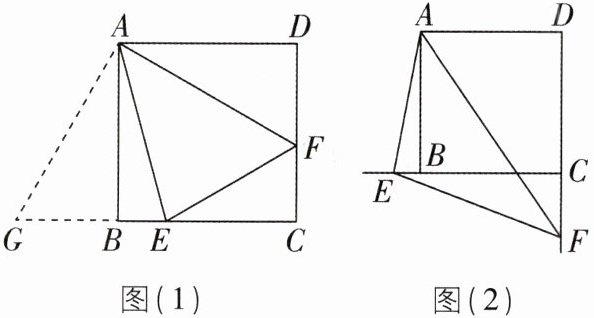
【初步探究】如图(1),在正方形ABCD中,点E,F分别在边BC,CD上,连接AE,AF,EF.若∠EAF= 45°,将△ADF绕点A顺时针旋转90°,得到△ABG.易证:△AEF≌△AEG.
(1)根据以上信息填空:
①∠EAG= ____°;
②线段BE,EF,DF之间满足的数量关系为____.
【迁移探究】
(2)如图(2),在正方形ABCD中,若点E在CB的延长线上,点F在DC的延长线上,∠EAF= 45°,猜想线段BE,EF,DF之间的数量关系,并证明.
【拓展探索】
(3)如图(3),已知正方形ABCD的边长为$3\sqrt {2}$,E,F分别在BC,CD上,∠EAF= 45°,连接BD分别交AE,AF于点M,N,若点M恰好为线段BD的三等分点,且BM<DM,求线段MN的长.


答案:
(1)
∵四边形ABCD是正方形,
∴∠D = ∠DAB = ∠ABC = 90°。
由旋转得∠ABG = ∠D = ∠ABE = 90°,∠GAB = ∠FAD,AG = AF,BG = DF,
∴G,B,E共线。
∵∠EAF = 45°,
∴∠EAG = ∠GAB + ∠BAE = ∠FAD + ∠BAE = 45° = ∠EAF。
在△EAF和△EAG中,$\left\{\begin{array}{l} AF = AG\\ ∠EAF = ∠EAG\\ AE = AE\end{array}\right.$,
∴△EAF≌△EAG(SAS),
∴EF = EG。
∵BE + BG = EG,
∴BE + DF = EF。故答案为①45,②BE + DF = EF。
(2)BE + EF = DF。证明如下:如图
(1),在DC上截取DH = BE,连接AH。
在△ABE和△ADH中,$\left\{\begin{array}{l} AB = AD\\ ∠ABE = ∠D = 90^{\circ }\\ BE = DH\end{array}\right.$,
∴△ABE≌△ADH(SAS),
∴AE = AH,∠BAE = ∠DAH,
∴∠BAE + ∠BAH = ∠BAH + ∠DAH = 90°,即∠EAH = ∠BAD = 90°。
∵∠EAF = 45°,
∴∠EAF = ∠FAH = 45°。
在△EAF和△HAF中,$\left\{\begin{array}{l} AE = AH\\ ∠EAF = ∠HAF\\ AF = AF\end{array}\right.$,
∴△EAF≌△HAF(SAS),
∴EF = HF。
∵DH + HF = DF,
∴BE + EF = DF。

(3)如图
(2),将△ADN绕点A顺时针旋转90°得到△ABK,连接KM。
∵四边形ABCD是正方形,
∴AB = AD = $3\sqrt{2}$,∠BAD = 90°,
∴∠ABD = ∠ADB = 45°,BD = $\sqrt{AB^{2}+AD^{2}} = 6$,
∴BM = $\frac{1}{3}BD = 2$,
∴DM = BD - BM = 4。
由旋转可得,∠KAN = 90°,AK = AN,BK = DN,∠ABK = ∠ADB = 45°,
∴∠KBM = ∠ABK + ∠ABD = 90°。
∵∠KAN = 90°,∠MAN = 45°,
∴∠KAM = ∠MAN = 45°。
又
∵AM = AM,
∴△AMK≌△AMN,
∴KM = MN。
设MK = MN = x,则BK = DN = 4 - x。
在Rt△BMK中,$BK^{2}+BM^{2}=MK^{2}$,
∴$(4 - x)^{2}+2^{2}=x^{2}$,解得x = 2.5,
∴MN = 2.5。

(1)
∵四边形ABCD是正方形,
∴∠D = ∠DAB = ∠ABC = 90°。
由旋转得∠ABG = ∠D = ∠ABE = 90°,∠GAB = ∠FAD,AG = AF,BG = DF,
∴G,B,E共线。
∵∠EAF = 45°,
∴∠EAG = ∠GAB + ∠BAE = ∠FAD + ∠BAE = 45° = ∠EAF。
在△EAF和△EAG中,$\left\{\begin{array}{l} AF = AG\\ ∠EAF = ∠EAG\\ AE = AE\end{array}\right.$,
∴△EAF≌△EAG(SAS),
∴EF = EG。
∵BE + BG = EG,
∴BE + DF = EF。故答案为①45,②BE + DF = EF。
(2)BE + EF = DF。证明如下:如图
(1),在DC上截取DH = BE,连接AH。
在△ABE和△ADH中,$\left\{\begin{array}{l} AB = AD\\ ∠ABE = ∠D = 90^{\circ }\\ BE = DH\end{array}\right.$,
∴△ABE≌△ADH(SAS),
∴AE = AH,∠BAE = ∠DAH,
∴∠BAE + ∠BAH = ∠BAH + ∠DAH = 90°,即∠EAH = ∠BAD = 90°。
∵∠EAF = 45°,
∴∠EAF = ∠FAH = 45°。
在△EAF和△HAF中,$\left\{\begin{array}{l} AE = AH\\ ∠EAF = ∠HAF\\ AF = AF\end{array}\right.$,
∴△EAF≌△HAF(SAS),
∴EF = HF。
∵DH + HF = DF,
∴BE + EF = DF。

(3)如图
(2),将△ADN绕点A顺时针旋转90°得到△ABK,连接KM。
∵四边形ABCD是正方形,
∴AB = AD = $3\sqrt{2}$,∠BAD = 90°,
∴∠ABD = ∠ADB = 45°,BD = $\sqrt{AB^{2}+AD^{2}} = 6$,
∴BM = $\frac{1}{3}BD = 2$,
∴DM = BD - BM = 4。
由旋转可得,∠KAN = 90°,AK = AN,BK = DN,∠ABK = ∠ADB = 45°,
∴∠KBM = ∠ABK + ∠ABD = 90°。
∵∠KAN = 90°,∠MAN = 45°,
∴∠KAM = ∠MAN = 45°。
又
∵AM = AM,
∴△AMK≌△AMN,
∴KM = MN。
设MK = MN = x,则BK = DN = 4 - x。
在Rt△BMK中,$BK^{2}+BM^{2}=MK^{2}$,
∴$(4 - x)^{2}+2^{2}=x^{2}$,解得x = 2.5,
∴MN = 2.5。

查看更多完整答案,请扫码查看


