《2025年初中必刷题九年级数学上册北师大版》

1 [2025 山西运城期中,中]如图,菱形 $ABCD$ 的对角线长分别为 8 和 10,$P$ 是较短对角线 $AC$ 上任意一点(不与点 $A$,$C$ 重合),$PE// BC$ 交 $AB$ 于点 $E$,$PF// CD$ 交 $AD$ 于点 $F$,连接 $EF$,则阴影部分的面积是( )

A.12
B.20
C.40
D.80

答案：
B 【解析】
∵ 菱形 ABCD 的对角线互相垂直，且对角线长分别为 8 和 10，
∴ S菱形ABCD=$\frac{1}{2}$×8×10=40.
∵ 四边形 ABCD 是菱形，
∴ AB//CD，AD//BC，AB=BC=CD=AD. 在△ABC 和△CDA 中，{AB=CD，BC=DA，AC=CA}，
∴ △ABC≌△CDA(SSS)，
∴ S△ABC=S△CDA=$\frac{1}{2}$S菱形ABCD=$\frac{1}{2}$×40=20. 如图，设 EF 交 AP 于点 O.
∵ PE//BC，AF//BC，PF//CD，AE//CD，
∴ PE//AF，PF//AE，
∴ 四边形 AEPF 是平行四边形，∠OPF=∠OAE，
∴ OP=OA. 在△OPF 和△OAE 中，{∠OPF=∠OAE，OP=OA，∠POF=∠AOE}，
∴ △OPF≌△OAE(ASA)，
∴ S△OPF=S△OAE，
∴ S阴影=S四边形BEOC+S△OPF=S四边形BEOC+S△OAE=S△ABC=20. 故选 B.

2 [2025 福建宁德质检,中]如图,在菱形 $ABCD$ 和菱形 $CEFG$(点 $D$ 在边 $CG$ 上)中,$B$,$C$,$E$ 在一条直线上,连接 $AF$,$EG$ 相交于点 $P$,连接 $CP$. 若 $BC = 5$,$CE = 10$,$EG = 12$,则 $CP$ 的长是( )

A.8
B.9
C.$\sqrt{73}$
D.$2\sqrt{73}$

答案： C 【解析】连接 CF 交 EG 于 O，连接 DO.
∵ 四边形 ABCD 和四边形 CEFG 是菱形，BC=5，CE=10，
∴ CD=BC=AD=5，CG=FG=CE=10，CF⊥GE，OE=OG=$\frac{1}{2}$GE=6，OC=OF，AD//CE//GF，
∴ CO=$\sqrt{CE² - OE²}$=8.
∵ GD=CG - CD=5，
∴ CD=DG.
∵ OC=OF，
∴ OD 是△CGF 的中位线，
∴ OD//GF，OD=$\frac{1}{2}$GF=5.
∵ AD//GF，
∴ A，D，O 三点共线，
∴ AO=AD+OD=10，∠FGP=∠AOP，
∴ AO=GF=10.
∵ ∠FPG=∠APO，
∴ △FPG≌△APO(AAS)，
∴ OP=GP=$\frac{1}{2}$OG=3.
∵ CF⊥GE，
∴ CP=$\sqrt{OC² + OP²}$=$\sqrt{8² + 3²}$=$\sqrt{73}$. 故选 C.

3 [2024 江苏南通质检,中]将长方形纸片 $ABCD$ 按如图所示的方式折叠,恰好得到菱形 $AECF$. 若 $AB = 3$,则菱形 $AECF$ 的面积为______.

答案： 2$\sqrt{3}$ 【解析】已知四边形 AECF 是菱形，AB=3，设 BE=x，则 AE=3 - x=CE.
∵ 四边形 AECF 是菱形，
∴ ∠FCO=∠ECO.
∵ ∠ECO=∠ECB，
∴ ∠ECO=∠ECB=∠FCO=30°，
∴ 2BE=CE，
∴ CE=2x，
∴ 2x=3 - x，解得 x=1，
∴ CE=2. 由勾股定理得 BC²+BE²=EC²，
∴ BC=$\sqrt{EC² - BE²}$=$\sqrt{2² - 1²}$=$\sqrt{3}$. 又
∵ AE=3 - x=3 - 1=2，
∴ 菱形的面积是 AE·BC=2$\sqrt{3}$. 故答案为 2$\sqrt{3}$.

4 [中]如图,在菱形 $ABCD$ 中,$\angle ABC = 60^{\circ}$,$AB = 4$,$BD$ 为对角线,$E$ 为 $AD$ 的中点,$F$ 为 $BD$ 上的一个动点,则 $\triangle AEF$ 周长的最小值为______.

答案：
2 + 2$\sqrt{3}$ 【解析】如图，连接 CF，CE，AC.
∵ 四边形 ABCD 是菱形，
∴ AB=BC=CD=AD=4，∠ABD=∠CBD，∠ABC=∠ADC=60°，
∴ △ACD 是等边三角形.
∵ E 为 AD 的中点，
∴ CE⊥AD. 在△ABF 和△CBF 中，{AB=CB，∠ABF=∠CBF，BF=BF}，
∴ △ABF≌△CBF(SAS)，
∴ AF=CF，
∴ AF+EF=CF+EF，
∴ 当 C，F，E 三点共线，即 CF+EF=CE 时，AF+EF 的值最小.
∵ E 为 AD 的中点，
∴ ED=2，
∴ 在 Rt△CDE 中，CE=$\sqrt{CD² - DE²}$=$\sqrt{16 - 4}$=2$\sqrt{3}$，
∴ △AEF 周长的最小值为 AE+AF+EF=AE+CE=2 + 2$\sqrt{3}$. 故答案为 2 + 2$\sqrt{3}$.

5 [2025 辽宁铁岭质检,中]如图,在菱形 $ABCD$ 中,$\angle ABC = 120^{\circ}$,射线 $BM$ 以点 $B$ 为旋转中心,从 $BC$ 的位置开始逆时针旋转,旋转角为 $\alpha(0^{\circ}＜\alpha＜120^{\circ})$,点 $E$ 与点 $C$ 关于 $BM$ 成轴对称,连接 $AE$ 并延长与 $BM$ 交于点 $F$,连接 $CE$,$CF$,$DF$.
(1)试判断 $\triangle CEF$ 的形状,并说明理由；
(2)当点 $E$ 为 $AF$ 中点时,求此时旋转角 $\alpha$ 的度数.

答案：
【解】
(1)△CEF 是等边三角形，理由如下：如图
(1)，连接 BE.
∵ 四边形 ABCD 是菱形，
∴ AB=BC.
∵ E，C 关于 BM 对称，
∴ BC=BE，FE=FC，
∴ AB=BE，
∴ ∠BAE=∠BEA.
∵ BC=BE，
∴ ∠BEC=∠BCE. 在四边形 ABCE 中，∠ABC=120°，
∴ ∠BAE+∠AEC+∠BCE=2∠AEC=360° - 120°=240°，
∴ ∠AEC=120°，
∴ ∠CEF=60°. 又
∵ FE=FC，
∴ △CEF 是等边三角形.
(2)连接 AC，BD，AC 与 BD 交于点 O，如图
(2).
∵ E 为 AF 中点，
∴ AE=EF. 又
∵ △CEF 是等边三角形，
∴ CE=CF=EF，
∴ AE=CE，∠ECF=∠EFC，
∴ ∠EAC=∠ECA，
∴ 2∠ECA+2∠ECF=180°，
∴ ∠ACF=90°. 在菱形 ABCD 中，∠ABC=120°，AC⊥BD，
∴ ∠AOD=90°，∠ADB=∠BDC=$\frac{1}{2}$∠ADC=$\frac{1}{2}$∠ABC=60°，
∴ BD//CF，
∴ ∠BDC=∠DCF=60°. 又
∵ ∠ECF=60°，
∴ EC 与 CD 重合.
∵ 四边形 ABCD 是菱形，∠ABC=120°，
∴ ∠BCD=60°，
∴ △BCD 是等边三角形，
∴ ∠DBC=60°.
∵ BM⊥CD，
∴ BM 平分∠DBC，
∴ 旋转角 α=30°.

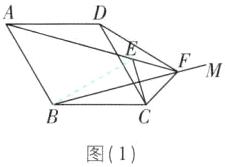
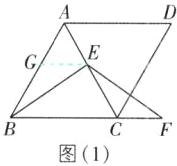
6 核心素养推理能力 [难]在菱形 $ABCD$ 中,$\angle ABC = 60^{\circ}$,$E$ 是对角线 $AC$ 上任意一点,$F$ 是线段 $BC$ 延长线上一点,且 $CF = AE$,连接 $BE$,$EF$.
(1)如图(1),当 $E$ 是线段 $AC$ 的中点时,$BE$ 和 $EF$ 的数量关系是______.
(2)如图(2),当点 $E$ 不是线段 $AC$ 的中点,其他条件不变时,请你判断(1)中的结论是否成立. 若成立,请给予证明；若不成立,请说明理由.
(3)如图(3),当点 $E$ 是线段 $AC$ 延长线上的任意一点,其他条件不变时,(1)中的结论是否成立？若成立,请给予证明；若不成立,请说明理由.

答案：
【解】
(1)
∵ 四边形 ABCD 是菱形，
∴ AB=BC.
∵ ∠ABC=60°，
∴ △ABC 是等边三角形，
∴ ∠BCA=60°. 又
∵ E 是线段 AC 的中点，
∴ ∠CBE=∠ABE=30°，AE=CE.
∵ CF=AE，
∴ CE=CF，
∴ ∠F=∠CEF=$\frac{1}{2}$∠BCA=30°，
∴ ∠CBE=∠F，
∴ BE=EF，故答案为 BE=EF.
(2)结论成立. 证明如下：过点 E 作 EG//BC 交 AB 于点 G，如图
(1)所示.
∵ 四边形 ABCD 为菱形，
∴ AB=BC，AB//CD.
∵ ∠ABC=60°，
∴ △ABC 为等边三角形，∠BCD=120°，
∴ ∠ACD=∠ACB=60°，∠DCF=∠ABC=60°，
∴ ∠ECF=120°.
∵ EG//BC，
∴ ∠AGE=∠ABC=60°. 又
∵ △ABC 为等边三角形，
∴ AB=AC，∠BAC=60°，
∴ △AGE 是等边三角形，
∴ AG=AE=GE，
∴ BG=CE，∠BGE=120°=∠ECF.
∵ CF=AE，
∴ GE=CF，
∴ △BGE≌△ECF(SAS)，
∴ BE=EF.

(3)结论成立. 证明如下：过点 E 作 EH//BC 交 AB 的延长线于点 H，如图
(2)所示.
∵ 四边形 ABCD 为菱形，
∴ AB=BC.
∵ ∠ABC=60°，
∴ △ABC 是等边三角形，
∴ AB=AC，∠ACB=∠BAC=60°，
∴ ∠ECF=60°.
∵ EH//BC，
∴ ∠AHE=∠ABC=60°，
∴ △AHE 是等边三角形，
∴ AH=AE=HE，
∴ BH=CE，∠AHE=∠ECF.
∵ CF=AE，
∴ HE=CF，
∴ △BHE≌△ECF(SAS)，
∴ BE=EF.