《2025年初中必刷题九年级数学上册北师大版》

9核心素养推理能力[较难]已知矩形ABCD的对角线AC,BD相交于点O,点E是边AD上一点,连接BE,CE,OE,且BE= CE.
(1)如图(1),求证:△BEO≌△CEO;

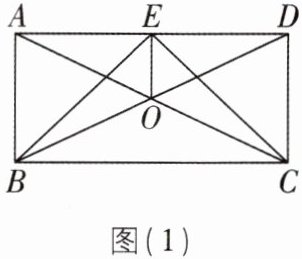
(2)如图(2),设BE与AC相交于点F,CE与BD相交于点H,过点D作AC的平行线交BE的延长线于点G,在不添加任何辅助线的情况下,请直接写出图(2)中的四个三角形(△AEF除外),使写出的每个三角形的面积都与△AEF的面积相等.

答案：
(1)【证明】
∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OB=OC=OA=OD.
∵BE=CE,OE=OE,
∴△BEO≌△CEO(SSS).
(2)【解】△DHE,△CHO,△DEG,△BFO的面积都与△AEF=∠CDA=90°,AB//CD,AB=DC.
∵BE=CE,
∴Rt△BAE≌Rt△CDE(HL),
∴∠AEB=∠DEC,AE=DE.
∵OA=OD,
∴∠OEA=∠OED=90°,
∴∠BAD=∠OED=90°,∠ADC=∠AEO=90°,
∴AB//OE//DC,
∴S△AEO=S△BEO,S△DEO=S△COE,
∴S△AEO - S△EFO=S△BEO - S△EFO,S△DEO - S△EHO=S△COE - S△EHO,
∴S△AEF=S△BFO,S△DHE=S△CHO.
∵OA=OD,
∴∠DAO=∠ADO.
∵△BEO≌△CEO,
∴∠BEO=∠CEO,
∴∠AEB=∠DEC,
∴△AEF≌△DEH(ASA),
∴S△AEF=S△DHE=S△CHO=S△BFO.
∵DG//AC,
∴∠G=∠AFE,∠GDE=∠FAE,
∴△AEF≌△DEG(AAS),
∴S△AEF=S△DEG.
∴△DHE,△CHO,△DEG,△BFO的面积都与△AEF的面积相等.

方法指导如图,在矩形ABCD中,AB= 3,BC= 2,O是AD的中点,连接OB,OC,点E在线段BC上(点E不与点B,C重合),过点E作EM⊥OB于M,EN⊥OC于N,求EM+EN的值.
解:连接OE.∵四边形ABCD是矩形,∴CD= AB= 3,AD= BC= 2,∠A= ∠D= 90°.
∵△OBE的面积+△OCE的面积= ______,
∴1/2OB·EM+1/2OC·EN= 1/2BC·AB,
∴1/2(EM+EN)×√{10}= 1/2×2×3,解得EM+EN= ______.

答案： △OBC的面积 $\frac{3\sqrt{10}}{5}$

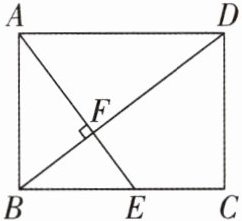
1[2025广西玉林期末,中]如图,在矩形ABCD中,AB= 3,BC= 4,AE⊥BD于F,则线段AF的长是 ( )

A.3
B.2.5
C.2.4
D.2

答案： C

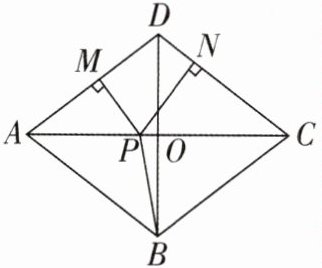
2[2024陕西咸阳秦都区调研,较难]如图所示,四边形ABCD中,AC⊥BD于点O,AO= CO= 4,BO= DO= 3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,PN⊥DC于点N.连接PB,在点P运动过程中,PM+PN+PB的最小值等于______.

答案： 7.8