第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1[2025江苏南京期末]周老师平时上班有A,B两条路线可以选择,她记录了两周共十天的上班路上所用的时间并绘制了如下统计图:
第一周上班选择路线A所用时间折线统计图
第二周上班选择路线B所用时间折线统计图
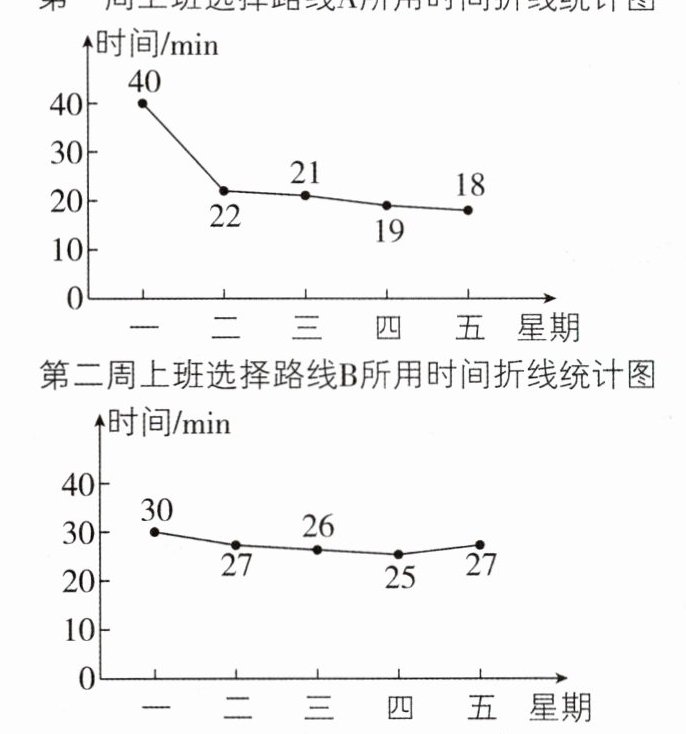
(1)这十天中周老师上班路上所用时间最多相差____min.
(2)哪一条上班路线所用的时间更稳定?请通过计算说明.
(3)你建议周老师应如何选择上班路线?
第一周上班选择路线A所用时间折线统计图
第二周上班选择路线B所用时间折线统计图

(1)这十天中周老师上班路上所用时间最多相差____min.
(2)哪一条上班路线所用的时间更稳定?请通过计算说明.
(3)你建议周老师应如何选择上班路线?
答案:
(1)22
(2)路线B所用的时间更稳定。理由如下:记第一周上班选择路线A所用时间的平均数和方差分别为$\overline {x}_{A},s_{A}^{2}$,第二周上班选择路线B所用时间的平均数和方差分别为$\overline {x}_{B},s_{B}^{2}$.$\overline {x}_{A}=\frac {1}{5}×(40 + 22 + 21 + 19 + 18)=24(min)$,$\overline {x}_{B}=\frac {1}{5}×(30 + 27 + 26 + 25 + 27)=27(min)$.$s_{A}^{2}=\frac {1}{5}×[(40 - 24)^{2}+(22 - 24)^{2}+(21 - 24)^{2}+(19 - 24)^{2}+(18 - 24)^{2}]=66$,$s_{B}^{2}=\frac {1}{5}×[(30 - 27)^{2}+(27 - 27)^{2}+(26 - 27)^{2}+(25 - 27)^{2}+(27 - 27)^{2}]=2.8$.因为2.8 < 66,即$s_{B}^{2}<s_{A}^{2}$,所以路线B所用的时间更稳定.
(3)对比这两周的折线统计图,建议周老师星期一上班选择路线B,星期二到星期五上班选择路线A.(建议合理即可)
(1)22
(2)路线B所用的时间更稳定。理由如下:记第一周上班选择路线A所用时间的平均数和方差分别为$\overline {x}_{A},s_{A}^{2}$,第二周上班选择路线B所用时间的平均数和方差分别为$\overline {x}_{B},s_{B}^{2}$.$\overline {x}_{A}=\frac {1}{5}×(40 + 22 + 21 + 19 + 18)=24(min)$,$\overline {x}_{B}=\frac {1}{5}×(30 + 27 + 26 + 25 + 27)=27(min)$.$s_{A}^{2}=\frac {1}{5}×[(40 - 24)^{2}+(22 - 24)^{2}+(21 - 24)^{2}+(19 - 24)^{2}+(18 - 24)^{2}]=66$,$s_{B}^{2}=\frac {1}{5}×[(30 - 27)^{2}+(27 - 27)^{2}+(26 - 27)^{2}+(25 - 27)^{2}+(27 - 27)^{2}]=2.8$.因为2.8 < 66,即$s_{B}^{2}<s_{A}^{2}$,所以路线B所用的时间更稳定.
(3)对比这两周的折线统计图,建议周老师星期一上班选择路线B,星期二到星期五上班选择路线A.(建议合理即可)
2[2025山东淄博期中]某中学广播站计划招一批广播员,有19名学生报名参加选拔.报名的学生需进行普通话、情境表达、个人才艺三项测试,每项测试均由五位评委打分(满分100分),取平均数作为该项的测试成绩,再按普通话占50%,情境表达占30%,个人才艺占20%计算出每人的总评成绩.根据以下图表解答相关问题.
表1:1号和2号选手的三项测试成绩和总评成绩统计表:
|选手|测试成绩/分|总评成绩/分|
| |普通话|情境表达|个人才艺| |
|1号|80|75|85|79.5|
|2号|86|80|★|★|
表2:1号和2号选手的个人才艺测试评委评分、平均数和方差统计表:
|选手|评委评分/分|平均数/分|方差|
|1号|85,80,83,90,87|85|$s_{1}^{2}$|
|2号|85,84,84.5,84,87.5|★|$s_{2}^{2}$|
(1)利用表2数据作答:
①2号选手的评委评分的众数是____分,平均数是____分.
②求$s_{1}^{2}和s_{2}^{2}$的值,并比较大小.
(2)计算2号选手的总评成绩.
(3)如图是这19名学生总评成绩的频数直方图(不完整),学校决定根据总评成绩x择优选拔9名广播员.(A:$60\leqslant x<70$;B:$70\leqslant x<80$;C:$80\leqslant x<90$;D:$90\leqslant x\leqslant 100$)
①补充完整总评成绩频数直方图.
②试分析1号、2号选手是否入选,并说明理由.
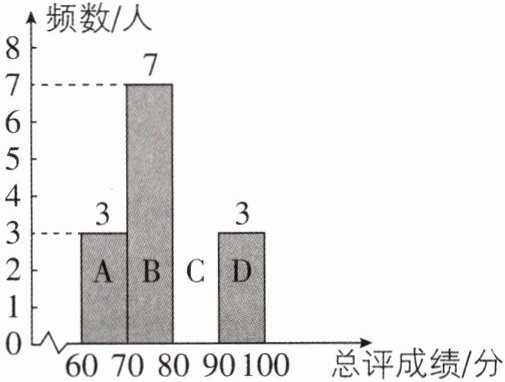
表1:1号和2号选手的三项测试成绩和总评成绩统计表:
|选手|测试成绩/分|总评成绩/分|
| |普通话|情境表达|个人才艺| |
|1号|80|75|85|79.5|
|2号|86|80|★|★|
表2:1号和2号选手的个人才艺测试评委评分、平均数和方差统计表:
|选手|评委评分/分|平均数/分|方差|
|1号|85,80,83,90,87|85|$s_{1}^{2}$|
|2号|85,84,84.5,84,87.5|★|$s_{2}^{2}$|
(1)利用表2数据作答:
①2号选手的评委评分的众数是____分,平均数是____分.
②求$s_{1}^{2}和s_{2}^{2}$的值,并比较大小.
(2)计算2号选手的总评成绩.
(3)如图是这19名学生总评成绩的频数直方图(不完整),学校决定根据总评成绩x择优选拔9名广播员.(A:$60\leqslant x<70$;B:$70\leqslant x<80$;C:$80\leqslant x<90$;D:$90\leqslant x\leqslant 100$)
①补充完整总评成绩频数直方图.
②试分析1号、2号选手是否入选,并说明理由.

答案:
(1)①84 85
②$s_{1}^{2}=\frac {1}{5}×[(85 - 85)^{2}+(80 - 85)^{2}+(83 - 85)^{2}+(90 - 85)^{2}+(87 - 85)^{2}]=11.6$,$s_{2}^{2}=\frac {1}{5}×[(85 - 85)^{2}+(84 - 85)^{2}+(84.5 - 85)^{2}+(84 - 85)^{2}+(87.5 - 85)^{2}]=1.7$,所以$s_{1}^{2}>s_{2}^{2}$
(2)2号选手的总评成绩为$86×50\% + 80×30\% + 85×20\% = 84$(分).
(3)①C组人数为19 - 3 - 7 - 3 = 6(人),补充完整总评成绩频数直方图如下:

②1号选手没有入选,2号选手入选.理由:由总评成绩频数分布直方图可得择优选拔的9名广播员的总评成绩应在C:$80≤x<90$;D:$90≤x≤100$两组内,而1号选手的总评成绩为79.5分,不在C、D两组范围内,2号选手的总评成绩为84分,在C组范围内,所以1号选手没有入选,2号选手入选.
(1)①84 85
②$s_{1}^{2}=\frac {1}{5}×[(85 - 85)^{2}+(80 - 85)^{2}+(83 - 85)^{2}+(90 - 85)^{2}+(87 - 85)^{2}]=11.6$,$s_{2}^{2}=\frac {1}{5}×[(85 - 85)^{2}+(84 - 85)^{2}+(84.5 - 85)^{2}+(84 - 85)^{2}+(87.5 - 85)^{2}]=1.7$,所以$s_{1}^{2}>s_{2}^{2}$
(2)2号选手的总评成绩为$86×50\% + 80×30\% + 85×20\% = 84$(分).
(3)①C组人数为19 - 3 - 7 - 3 = 6(人),补充完整总评成绩频数直方图如下:

②1号选手没有入选,2号选手入选.理由:由总评成绩频数分布直方图可得择优选拔的9名广播员的总评成绩应在C:$80≤x<90$;D:$90≤x≤100$两组内,而1号选手的总评成绩为79.5分,不在C、D两组范围内,2号选手的总评成绩为84分,在C组范围内,所以1号选手没有入选,2号选手入选.
3AI DPSK原创甲、乙、丙、丁四名学生竞赛成绩(单位:分)如下:15,18,15,24,按照“组内离差平方和最小”的方法,将竞赛成绩分成两组.
答案:
将4个数据从小到大排序:15,15,18,24.把4个数据分成两组,共有3种情况:第一种情况,第一组1个数据{15},组内离差平方和为0;第二组3个数据{15,18,24},平均数是19,组内离差平方和为$(15 - 19)^{2}+(18 - 19)^{2}+(24 - 19)^{2}=42$,故第一种情况的组内离差平方和为0 + 42 = 42.第二种情况,第一组2个数据{15,15},平均数是15,组内离差平方和为0;第二组2个数据{18,24},平均数是21,组内离差平方和为$(18 - 21)^{2}+(24 - 21)^{2}=18$,故第二种情况的组内离差平方和为0 + 18 = 18.第三种情况,第一组3个数据{15,15,18},平均数是16,组内离差平方和为$(15 - 16)^{2}+(15 - 16)^{2}+(18 - 24)^{2}=38$;第二组1个数据{24},组内离差平方和为0,故第三种情况的组内离差平方和为0 + 38 = 38.因为18 < 38 < 42,所以第二种情况的组内离差平方和最小,所以将竞赛成绩分成的两组是{15,15},{18,24}.
查看更多完整答案,请扫码查看


