《2025年初中必刷题八年级数学上册北师大版》

一、选择题(本大题共8小题,每小题4分,共32分)
1 [2024山东烟台中考]下列实数中的无理数是( )

A.$\frac{2}{3}$
B.3.14
C.$\sqrt{15}$
D.$\sqrt[3]{64}$

答案： C 【解析】A选项，$\frac{2}{3}$是有理数，不符合题意；B选项，3.14是有理数，不符合题意；C选项，$\sqrt{15}$是无理数，符合题意；D选项，$\sqrt[3]{64}=4$是有理数，不符合题意。故选C。

2 [2025辽宁鞍山质检]下列算式中,正确的是( )

A.$\sqrt{2}+\sqrt{3}= \sqrt{5}$
B.$3\sqrt{2}-\sqrt{2}= 2\sqrt{2}$
C.$\sqrt{\frac{4}{3}}÷\sqrt{\frac{1}{9}}= 3\sqrt{2}$
D.$\sqrt{4+\frac{1}{2}}= 2+\sqrt{\frac{1}{2}}$

答案： B 【解析】$\sqrt{2}$与$\sqrt{3}$不能合并，故A选项运算错误，不符合题意；$3\sqrt{2}-\sqrt{2}=2\sqrt{2}$，故B选项运算正确，符合题意；$\sqrt{\frac{4}{3}}÷\sqrt{\frac{1}{9}}=\sqrt{\frac{4}{3}÷\frac{1}{9}}=\sqrt{\frac{4}{3}×9}=\sqrt{12}=2\sqrt{3}$，故C选项运算错误，不符合题意；$\sqrt{4+\frac{1}{2}}=\sqrt{\frac{9}{2}}=\frac{3\sqrt{2}}{2}$，故D选项运算错误，不符合题意。故选B。

3 [2025广西钦州质检]若$a= \frac{1}{\sqrt{2}-1}$,$b= \frac{1}{\sqrt{2}+1}$,则$\sqrt{ab}(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}})$的值为( )

A.2
B.-2
C.$\sqrt{2}$
D.$2\sqrt{2}$

答案： A 【解析】$a=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$，$b=\frac{1}{\sqrt{2}+1}=\sqrt{2}-1$，原式$=\sqrt{a}\cdot\sqrt{b}(\frac{\sqrt{a}}{\sqrt{b}}-\frac{\sqrt{b}}{\sqrt{a}})=a - b=(\sqrt{2}+1)-(\sqrt{2}-1)=2$。故选A。

4 [2025福建三明期中]若$\sqrt{12n}$是整数,则正整数n的最小值是( )

A.3
B.4
C.5
D.6

答案： A 【解析】因为$\sqrt{12n}$是整数，$12 = 2^{2}×3$，所以正整数n的最小值是3。故选A。

5 已知x,y为实数,且$\sqrt{2x+5}+(y-2)^{2}= 0$.若$axy-2x= y$,则实数a的值为( )

A.$\frac{3}{5}$
B.$\frac{5}{3}$
C.$\frac{2}{5}$
D.$\frac{5}{2}$

答案： A 【解析】因为$\sqrt{2x + 5}+(y - 2)^{2}=0$，所以$2x + 5 = 0$，$y - 2 = 0$，解得$x = - 2.5$，$y = 2$。因为$axy - 2x = y$，所以$-2.5×2a - 2×(-2.5)=2$，所以$-5a + 5 = 2$，解得$a=\frac{3}{5}$。

6 [2025江苏常州期中]对于实数x,我们规定[x]表示不大于x的最大整数,如[2]= 2,[1.5]= 1,[-2.3]= -3.对数99进行如下操作:99$\xrightarrow{第1次}$[$\sqrt{99}$]= 9$\xrightarrow{第2次}$[$\sqrt{9}$]= 3$\xrightarrow{第3次}$[$\sqrt{3}$]= 1,这样只需对数99进行3次操作后即可变成1,类似地,使数2024变成1需要进行操作的次数是( )

A.3
B.4
C.5
D.6

答案： B 【解析】$2024\xrightarrow[]{第1次}[\sqrt{2024}]=44\xrightarrow[]{第2次}[\sqrt{44}]=6\xrightarrow[]{第3次}[\sqrt{6}]=2\xrightarrow[]{第4次}[\sqrt{2}]=1$，则数2024进行4次操作后变成1。故选B。

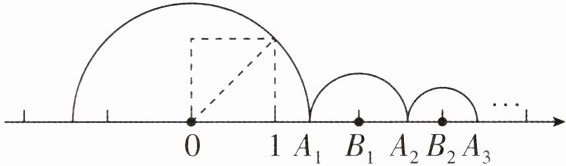
7 [2025浙江温州期末]如图,通过画边长为1的正方形,就能准确地把$\sqrt{2}表示在数轴上的点A_{1}$处,记$A_{1}右侧最近的整数点为B_{1}$,以点$B_{1}$为圆心,$A_{1}B_{1}$为半径画半圆,交数轴于点$A_{2}$,记$A_{2}右侧最近的整数点为B_{2}$,以点$B_{2}$为圆心,$A_{2}B_{2}$为半径画半圆,交数轴于点$A_{3}$,如此继续,则$A_{8}B_{8}$的长为( )


A.$\sqrt{2}-1$
B.$\sqrt{2}$
C.$\sqrt{2}+1$
D.$2-\sqrt{2}$

答案： A 【解析】由题意得$A_{1}B_{1}=2-\sqrt{2}$，则点$A_{2}$表示的数为$2 + 2-\sqrt{2}=4-\sqrt{2}$。因为$2＜4-\sqrt{2}＜3$，所以点$B_{2}$表示的数为3，所以$A_{2}B_{2}=\sqrt{2}-1$，同理可得$A_{3}B_{3}=2-\sqrt{2}$，$A_{4}B_{4}=\sqrt{2}-1$，$A_{5}B_{5}=2-\sqrt{2}$，$A_{6}B_{6}=\sqrt{2}-1$，$A_{7}B_{7}=2-\sqrt{2}$，$A_{8}B_{8}=\sqrt{2}-1$。故选A。

8 $a= 2019×2021-2019×2020$,$b= \sqrt{2022^{2}-4×2021}$,$c= \sqrt{2020^{2}+20}$,则a,b,c的大小关系是( )

A.$a＜b＜c$
B.$a＜c＜b$
C.$b＜a＜c$
D.$b＜c＜a$

答案： A 【解析】$a = 2019×2021 - 2019×2020=(2020 - 1)(2020 + 1)-(2020 - 1)×2020=2020^{2}-1 - 2020^{2}+2020=2019$。因为$2022^{2}-4×2021=(2021 + 1)^{2}-4×2021=2021^{2}+2×2021 + 1 - 4×2021=2021^{2}-2×2021 + 1=(2021 - 1)^{2}=2020^{2}$，所以$b = 2020$。因为$\sqrt{2020^{2}+20}＞\sqrt{2020^{2}}$，所以$c＞b＞a$。故选A。

二、填空题(本大题共4小题,每小题5分,共20分)
9 [2025陕西西安期中]张师傅将一个体积为28$cm^{3}$的铁块和一个体积为36$cm^{3}$的铁块熔铸成一个大正方体铁块,若熔铸过程无损耗,则熔铸成的大正方体铁块的棱长是______cm.

答案： 4 【解析】由题意知，这个大正方体铁块体积为$28 + 36 = 64(cm^{3})$，所以熔铸成的大正方体铁块的棱长是$\sqrt[3]{64}=4(cm)$。故答案为4。

10 [2025河南周口期中]若“输入x→取立方根→取算术平方根→输出2”,则x的值为______.

答案： 64 【解析】因为2是4的算术平方根，4的立方为64，所以x的值为64。故答案为64。

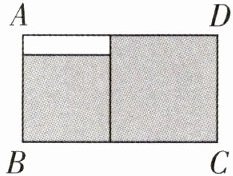
11 如图,在长方形ABCD中无重叠地放入面积分别为16$cm^{2}$和12$cm^{2}$的两张正方形纸片(图中阴影部分),则图中空白部分的面积为______$cm^{2}$.

答案： $(8\sqrt{3}-12)$ 【解析】因为两张正方形纸片的面积分别为$16cm^{2}$和$12cm^{2}$，所以它们的边长分别为$\sqrt{16}=4(cm)$，$\sqrt{12}=2\sqrt{3}(cm)$，所以空白部分的面积为$2\sqrt{3}×(4 - 2\sqrt{3})=(8\sqrt{3}-12)cm^{2}$。故答案为$(8\sqrt{3}-12)$。

12 已知$\sqrt{16-x^{2}}-\sqrt{4-x^{2}}= 2\sqrt{2}$,则$\sqrt{16-x^{2}}+\sqrt{4-x^{2}}$= ______.

答案：
$3\sqrt{2}$ 【解析】

13 计算:
(1)$(\sqrt{5}-\sqrt{2})(\sqrt{5}+\sqrt{2})-(\sqrt{3}-1)^{2}$;
(2)$\sqrt{48}÷\sqrt{3}-\sqrt{\frac{1}{2}}×\sqrt{12}+\sqrt{24}$.

答案： 【解】
(1)原式$=5 - 2-(3 - 2\sqrt{3}+1)=3 - 3 + 2\sqrt{3}-1=2\sqrt{3}-1$。
(2)原式$=\sqrt{48÷3}-\sqrt{\frac{1}{2}×12}+2\sqrt{6}=4-\sqrt{6}+2\sqrt{6}=4+\sqrt{6}$。